12. Правильний та неправильний умовивід

Умовами здобуття істинних висновків в умовиводі є: 1) істинність вихідних висловлювань або засновків; 2) правильність виводу. Поняття істинного висловлювання (судження) розглядалось нами в модулі IV - "Просте судження". Поняття ж "правильності виводу" пов'язане з відношенням логічного слідування. Для розкриття його змісту проаналізуємо таке міркування: "Якщо я склав залік з логіки (А) та залік з історії України (В), отже, я можу стверджувати, що я напевно склав залік з логіки або історії України". Логічна структура цього міркування є такою: "Якщо А і В, отже, А або В".

Таким чином, правильним умовивід є тоді і тільки тоді, коли висновок є логічним наслідком із засновків. У таку структуру ми можемо замість А і В поставити будь-які за змістом істинні твердження і завжди будемо отримувати істинний висновок.

Отже, неправильним називають такий умовивід, у якому між засновками та висновком не існує відношення логічного слідування. Такий умовивід не гарантує істинного висновку при істинних засновках.

13. Обернення судження

Нагадаємо, що дедуктивні умовиводи поділяються на виводи логіки висловлювань (виводи зі складних суджень) та виводи з простих категоричних суджень (А, Е, І, О), які мають структуру "Б-Р". Виводи з простих категоричних суджень поділяють на опосередковані - з двох і більше суджень-засновків, та безпосередні з одного судження-засновку.

У даному і подальших параграфах цього розділу ми будемо розглядати безпосередні умовиводи.

* Безпосередніми умовиводами називають такі дедуктивні виводи, які здійснюються з одного категоричного судження-засновку.

Існують чотири основних види безпосереднього виводу:

1) обернення судження; 2) перетворення судження; 3) протиставлення предикатові та 4) виводи за логічним квадратом.

Обернення - це логічна операція, в результаті якої Б та Р судження-засновку міняються місцями. Якість судження при оберненні не змінюється. Якщо кількість судження не змінюється, то таке обернення називають простим, або чистим. Якщо ж кількість судження при оберненні змінюється, то таке обернення називають оберненням з обмеженням (узагальненням).

Залежно від чотирьох типів простих категоричних суджень існують такі правила обернення суджень.

Загальностверджувальне судження.

А(8Р) -" А(РБ): "Усі Б є Р, отже, всі Р є 8".

Наприклад:

Це приклад чистого обернення.

А($Р) -" І(Р8): "Усі Б є Р, отже, деякі Р є Б".

Це приклад обернення з обмеженням. Загальнозаперечне судження.

Е(8Р) -" Е(Р8): "Жодне 8 не є Р, отже, жодне Р не є 8". Наприклад:

Частковостверджувальне судження. I(SP) -> I(PS): "Деякі S є Р, отже, деякі Р є S". Наприклад:

КБР) -> А(РБ): "Деякі 8 є Р, отже, всі Р є 8". Наприклад:

Це приклад обернення з узагальненням.

Частковозаперечне судження не завжди дає необхідні виводи у випадку обернення, тобто висновки обернення з судження 0(8Р) не завжди є істинними. Наприклад: "Деякі злочинці не є рецидивістами, отже, деякі рецидивісти не є злочинцями (?!)". Виходячи з цього, частковозаперечне судження операції обернення не підлягає.

Перетворення судження

Перетворення - це логічна операція, в результаті якої судження змінює свою якість, а предикат висновку заперечує предикат засновку. Кількість судження при цьому не змінюється.

У залежності від чотирьох типів простих категоричних суджень існують такі правила перетворення суджень.

Загальностверджувальне судження.

А(8Р) —> Е(8 - Р): "Усі 8 є Р, отже, жодне 8 не є не Р".

Основою утворення умовиводу тут виступає закономірність відношення обсягів двох суперечливих понять, які є предикатами одного і того самого суб'єкта. Відомо, що два суперечливих поняття (Р і ~Р) завжди вичерпують обсяг свого родового поняття. Якщо відомо, що даний предмет входить до обсягу Р, то це є підставою для висновку, що він не входить до обсягу ~Р, і навпаки. Подвійне заперечення (не є не Р), що використовується у судженні-висновку означає рівнозначність цих двох суджень.

Наприклад:

А Усі адвокати - юристи.

Е Жоден адвокат не є не юристом.

Загальнозаперечне судження.

E(SP) -> A(S ~Р): "Жодне S не є Р, отже, всі S є не Р".

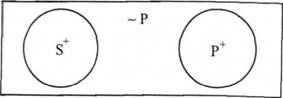
Наприклад:

Жодна кішка не є собакою. Усі кішки є не собаками.

Частковостверджувальне судження.

1(SP) —"0(S ~Р): "Деякі S є Р, отже, деякі S не є не Р".

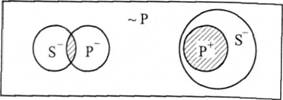
Наприклад:

Деякі студенти є відмінниками. Деякі студенти не є не відмінниками.

Частковозаперечне судження.

О(БР) -> 1(5 ~Р): "Деякі Б не є Р, отже, деякі Б є не Р".

Наприклад:

Деякі жінки не є депутатами. Деякі жінки є не депутатами.

6. Протиставлення предикатові

Протиставлення предикатові - це логічна операція, яка складається з двох попередніх, тобто: 1) судження змінює якість на протилежну, а в деяких випадках змінюється і кількість судження; 2) Б та Р судження-висновку міняються місцями; 3) Р висновку є поняттям, заперечним (~Р) до Р засновку.

У залежності від чотирьох типів простих категоричних суджень існують такі правила протиставлення предикатові.

Загальностверджувальне судження.

А(8Р) —" Е(~ РБ): "Усі 8 є Р, отже, жодне не Р не є 5".

Наприклад:

Усі правильні трикутники є рівнобічними. Жоден нерівнобічний трикутник не є правильним.

Загальнозаперечне судження.

E(SP) -> I(~PS): "Жодне S не є Р, деякі не Р є S".

Наприклад:

Жоден кит не є рибою. Деякі не риби є китами.

Оскільки, в поняття "не риби" включається багато видів тварин (крім китів), то ми кажемо "деякі", але не "всі". Частковозаперечне судження. 0(8Р) -"І(~Р8): "Деякі 8 не є Р, отже, деякі не Р є 8 ".

Наприклад:

Деякі злочинці не є повнолітніми. Деякі неповнолітні є злочинцями.

Частковостверджувальне судження не завжди дає необхідні виводи при протиставленні предикатові, тобто висновки з протиставлення предикатові судження І(8Р) не завжди є істинними (а часто навіть позбавлені здорового глузду). Наприклад: "Деякі люди є вегетаріанцями, отже, деякі невегетаріанці не є людьми (?!)". Виходячи з цього, частково-стверджувальне судження протиставленню предикатові не підлягає.