5.2.3. Случай неколлинеарных скоростей и
В ситуации, изображенной на рисунке 3.14.7, скорости и не коллинеарны.
Рис.3.14.7
Тогда точка должна находиться на прямых, ортогональных скоростям и .
Если через точку и точку проведем прямые, ортогональные и , то их пересечение даст единственную точку .
Очевидно, построенная таким образом точка совпадает с МЦС.
Данное утверждение следует из того факта, что МЦС должен находиться на указанных перпендикулярах, а также из теоремы существования и единственности МЦС.
Примечание
Следует иметь в виду, что согласно следствию 1 из формулы Эйлера для заданных скоростей и должно выполняться равенство
,
где
.
Поэтому
прежде, чем делать построение МЦС, в
ситуации, изображенной на рисунке
3.14.7, следует сначала проверить выполнение
равенства проекций заданных скоростей
и
на прямую
с направляющим вектором
.
Если проекции не равны по величине или противоположны по направлению, то задача построения МЦС в данной ситуации не имеет решения, так как исходные данные некорректны.
6º. Мгновенный центр ускорений
Определение 6
Точка плоскости плоской фигуры, имеющая ускорение, равное нулю в момент времени , называется мгновенным центром ускорений (МЦУ).
Теорема 3
Если
в некоторый момент времени
справедливы соотношения
и
,
то в этот момент времени существует
единственная точка
плоской фигуры, ускорение которой равно
нулю.
Доказательство
Согласно
формуле Ривальса,
для любой точки 
плоской фигуры можем записать:
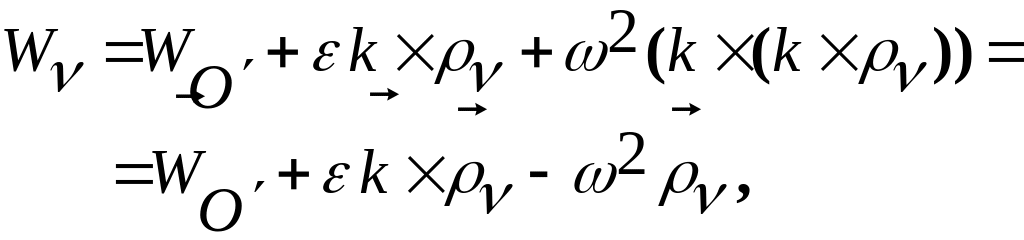(3.14.20)
где
,
.
Считая
известным, найдем из (3.14.20)
зависимость
от вектора
.
Для этого умножим (3.14.20) векторно на орт слева. Получим
.
Соединяя
с уравнением (3.14.20), приходим к системе
векторных уравнений относительно
и
:
,
.
Из
нее, умножая первое уравнение на
,
а второе на
и складывая, получим
.
Разрешая относительно , окончательно будем иметь
.
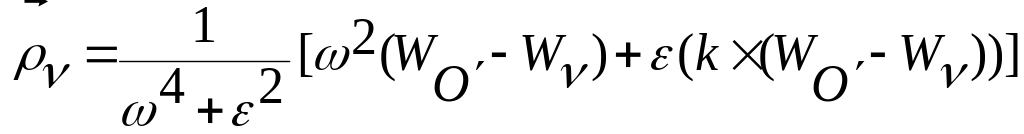Положим
в правой части
и тем самым найдем положение точки
,
которая будет иметь ускорение, равное
нулю.
Очевидно, такая точка единственная в силу однозначной зависимости от . Ее положение определяется формулой:
.
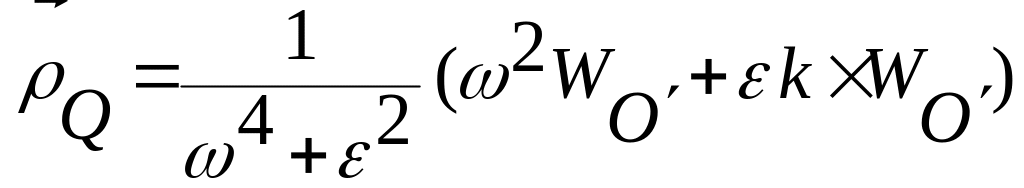Теорема доказана.
Замечание
Если точку принять за полюс связанной системы в момент , то формула Ривальса для ускорения любой точки плоской фигуры будет иметь вид:
,
где
,
,
— радиус-вектор точки
плоской фигуры относительно точки
.
Из нее находим величину ускорения
.