3.2. Векторный способ задания движения
Поскольку на движениях плоской фигуры выполняется тождество (3.14.9)
, (3.14.9)
то
согласно теореме, доказанной в §12 при
рассмотрении вращательного движения
твердого тела вокруг неподвижной оси,
матрица ориентации
плоской фигуры может быть задана одним
углом
.
Через этот угол
матрица
записывается в виде:
. (3.14.10)
Вектор
мгновенной угловой скорости
фигуры при этом связан с производной
по времени от угла
следующей зависимостью
. (3.14.11)
Обозначим
— положение точки
фигуры относительно подвижного полюса 
в момент времени
.
Тогда
ее движение относительно точки отсчета
задается вектор-функцией
.
Очевидно,
вектор-функция
связана с движением
точки
в абсолютном пространстве относительно
полюса
следующим соотношением
.
Здесь
— движение полюса
связанной системы координат относительно
точки отсчета
.
Из уравнений связей (3.14.7):
, , , (3.14.7)
следуют тождества
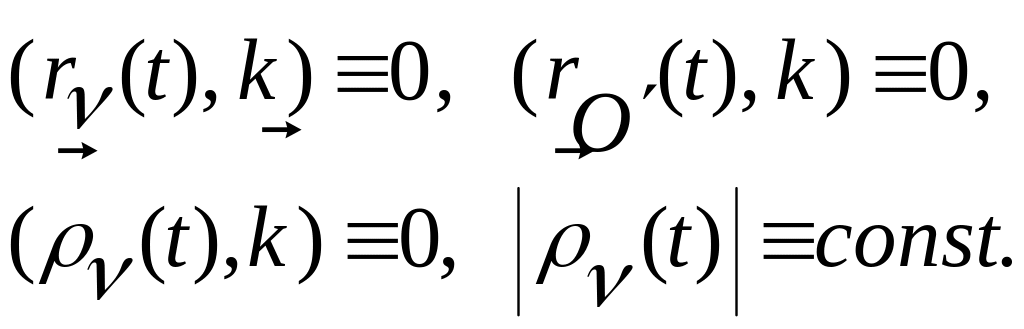(3.14.12)
На соотношения (3.14.12) можем смотреть как на ограничения движений точек фигуры, которые вытекают из определения плоской фигуры и из следующих ее свойств:
фигура является плоским абсолютно твердым телом;
она совершает движение по плоскости, совпадающей с плоскостью фигуры.
Поэтому векторную форму задания движения плоской фигуры можем записать, исходя из векторной формы задания движения, построенной для произвольного абсолютно твердого тела (см. (3.2.1) в §2).
Затем дополнить уравнения, указанные в этой форме, связями (3.14.12)
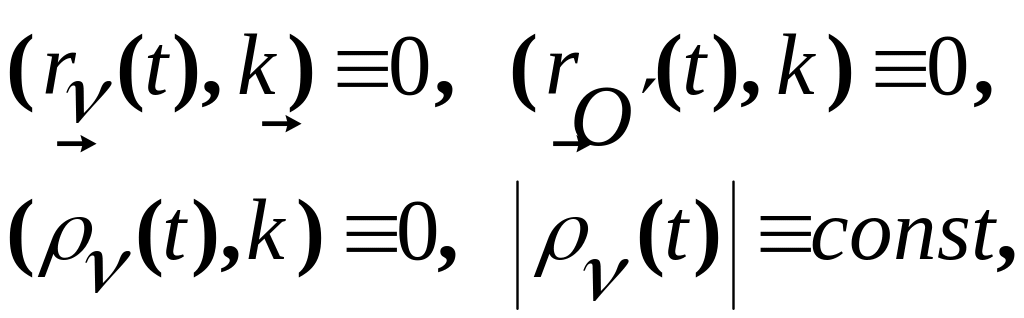(3.14.12)
справедливыми для плоской фигуры.
С учетом обозначений, принятых в данном параграфе, уравнения (3.2.1) в §2
(3.2.1)
применительно к плоской фигуре примут вид
,
,
, (3.14.13)
где
.
В них
обозначают координаты точки
в связанной системе (постоянные величины),
а
и
— вектор-функции, описывающие ориентацию
плоской фигуры.
Таким образом, соотношения (3.14.13) — это векторная форма задания движения плоской фигуры в абсолютном пространстве.
3.3. Координатный способ задания движения
Координатный способ задания движения плоской фигуры получим, если (3.14.13) запишем в проекциях на абсолютные оси.
Тогда с учетом (3.14.10)
. (3.14.10)
будем иметь:
(3.14.14)
Здесь
— движение полюса связанной системы
координат, заданное в координатной
форме, а
— угловое движение плоской фигуры.
Из (3.14.13):
, , , (3.14.13)
где
,
и
из (3.14.14) следует, что если
плоская фигура не является точкой,
то она имеет три степени свободы положения
(для описания любого ее движения
необходимо знать законы изменения трех
независимых координат
).
Если
плоская фигура — это точка,
то для описания любого ее движения
необходимо знать законы изменения двух
координат
и
.
Следовательно, в этом случае она имеет две степени свободы положения.