30

ЛЕКЦИЯ 14. КИНЕМАТИКА. Глава 3. (Лекция 5 по главе 3) §14. Стр.1-33. 31.07.2012

Глава 3. Кинематика твердого тела

§14. Плоское движение твердого тела

1º. Свойства плоского движения

Определение 1

Движение твердого тела называется плоским, если существует орт , неподвижный в абсолютном пространстве, такой, что на этом движении для любой точки твердого тела при всех выполняется тождество

, (3.14.1)

где — некоторая постоянная (быть может, своя для каждой точки  ).

В тождестве (3.14.1) — это вектор-функция, которой задается движение точки относительно точки отсчета на промежутке времени .

Если обозначим координаты точки  в некоторый момент времени в абсолютной системе координат  , а — направляющие косинусы орта в этой же системе, то тождество (3.14.1) запишется в виде следующего равенства, которое справедливо в любой момент времени на движениях точки :

. (3.14.2)

Из (3.14.2) можем сделать следующие выводы.

1. Каждая точка твердого тела движется в одной и той же плоскости, причем плоскости движения всех точек параллельны.

2. Скорость 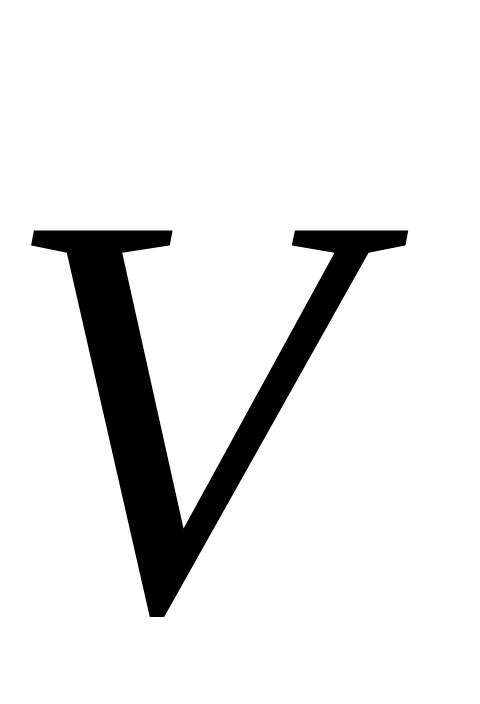и ускорение 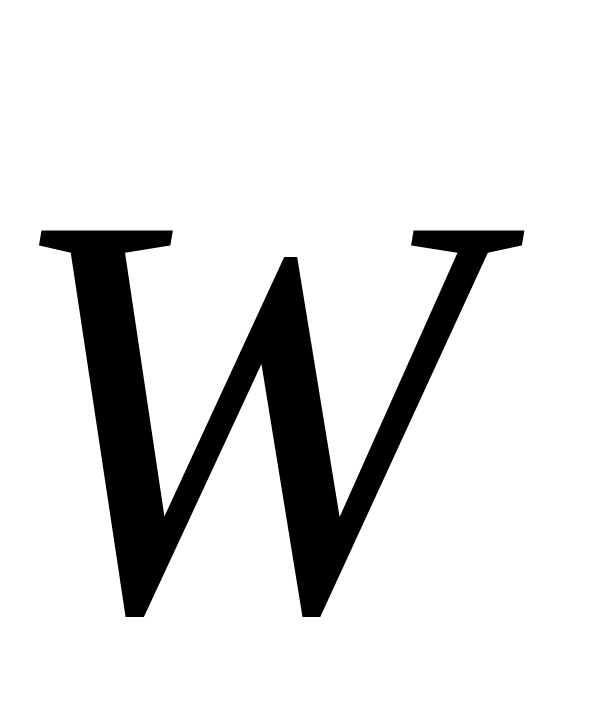этой точки находятся в той же плоскости.

3. Расстояние от полюса абсолютной системы до этой плоскости остается постоянным и равно модулю величины , ибо , где 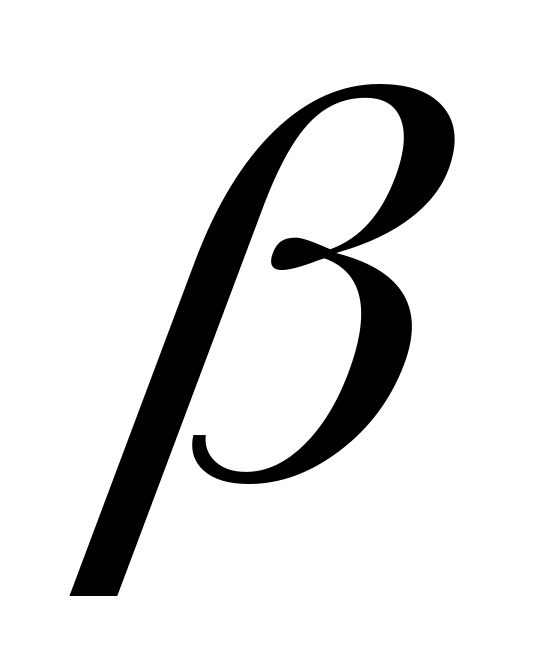— угол между векторо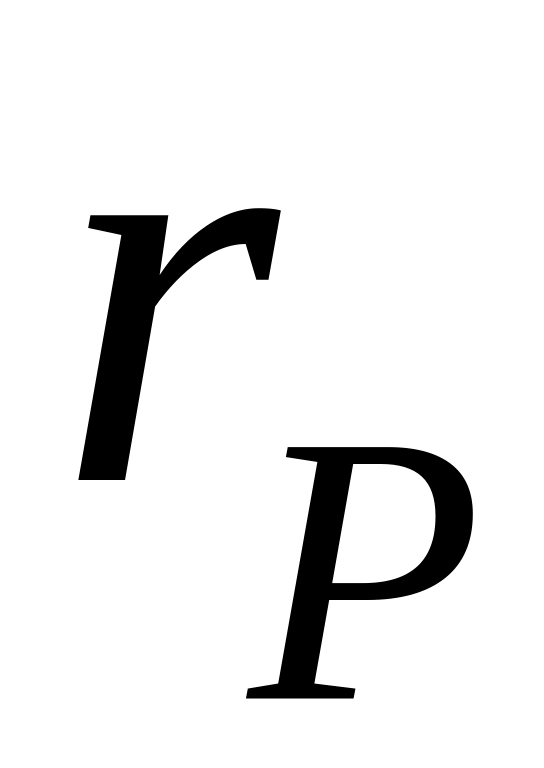м и ортом .

В качестве абсолютной системы координат возьмем систему , в которой орт совпадает с ортом , т.е. (см. рис. 3.14.1).

Точка  может быть любой фиксированной в абсолютном пространстве.

Представим вектор в виде суммы

. (3.14.3)

Здесь — точка, являющаяся ортогональной проекцией точки  на плоскость .

Легко видеть, что в равенстве (3.14.3) величина  задает расстояние полюса  до плоскости  , в которой происходит движение точки  .

Пусть — любая другая точка твердого тела, не совпадающая с точкой , и — положение точки в момент времени .

Обозначим ортогональную проекцию точки на плоскость , а — положение точки .

Рис.3.14.1

Можем записать

, (3.14.4)

где — постоянная, определяющая плоскость, в которой движется точка  .

Она задается в соответствии с формулой (3.14.1), в которой вместо следует подставить , а вместо — постоянную .

На основе формул (3.14.3) и (3.14.4)

, (3.14.3)

, (3.14.4)

легко доказываются следующие утверждения.

Следствие 1

На любом плоском движении твердого тела расстояние между точками и остается постоянным при всех .

Доказательство

Поскольку для точек и твердого тела справедливо уравнение связи

,

то, подставляя в него (3.14.3) и (3.14.4)

, (3.14.3)

, (3.14.4)

получим

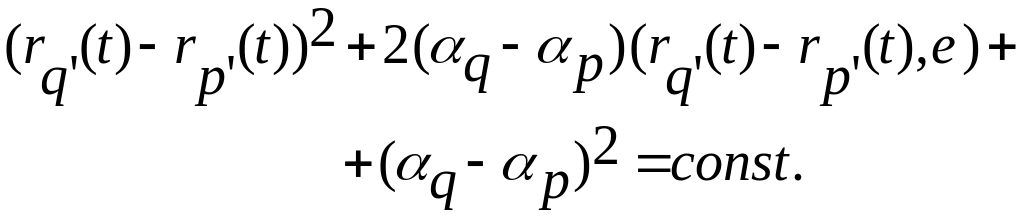(3.14.5)

Второе слагаемое равно нулю, так как , . Поскольку , то из (3.14.5) устанавливаем, что

.

Следствие 1 доказано.

Следствие 2

Если точки и в какой-либо момент времени находятся на прямой, параллельной орту , то и при всех они будут находиться на прямой, параллельной орту .

Иначе говоря, если положения точек и в некоторый момент времени совпадают, то и для всех при плоском движении твердого тела их положения будут совпадать.

Доказательство

Из условия следствия 2 в момент времени имеем:

,

ибо и совпадают в момент . А тогда согласно следствию 1 будет выполняться

при всех , т.е. . Это означает, что точки и совпадают при всех .

Следствие 2 доказано.

Следствие 3

Если точки и твердого тела в некоторый момент времени находятся на одной прямой, параллельной орту , то:

1. перемещение точки  за время 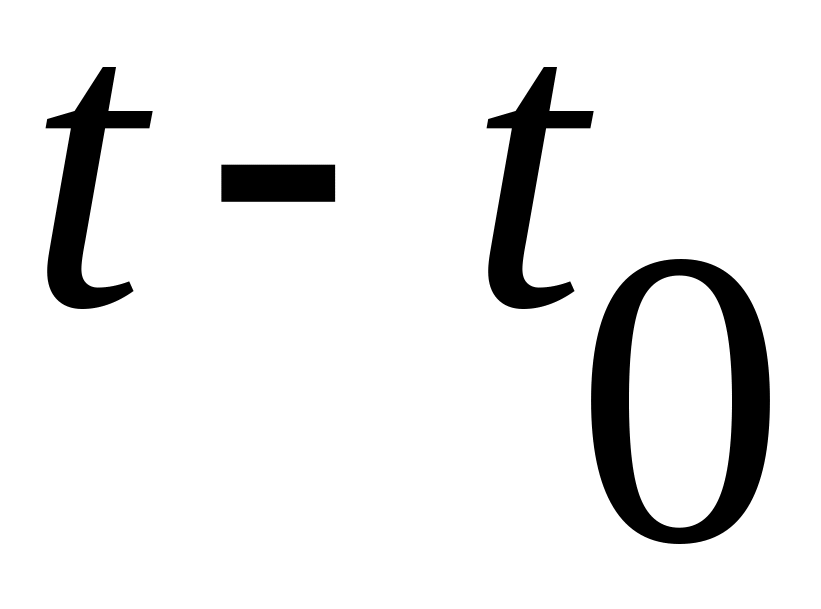совпадает с перемещением точки за это же время и равно

;

2. скорости точек и совпадают по величине и направлению со скоростью точки ;

3. ускорения точек и совпадают с ускорением точки .

Доказательство

Поскольку точки  и находятся на прямой, параллельной орту в момент времени , то согласно следствию 2 точки и совпадают в любой момент.

Поэтому в соотношениях (3.14.3) и (3.14.4)

, (3.14.3)

, (3.14.4)

равенство (3.14.4) можно записать так:

. (3.14.6)

А тогда из (3.14.3) и (3.14.6) следуют все утверждения следствия 3.

Действительно, по определению перемещения точки за время имеем

.

Подставляя равенство (3.14.3)

, (3.14.3)

записанное для моментов времени и , получим

.

Аналогично для точек и с учетом (3.14.4) будем иметь

.

По условию следствия 3 в момент времени точки и находятся на одной прямой, параллельной орту . Поэтому, согласно следствию 2, положения точек и совпадают при всех , т.е.

, .

А тогда

.

Утверждение 1) доказано.

Справедливость утверждений 2) и 3) будет установлена, если продифференцируем дважды по  соотношения (3.14.3) и (3.14.6):

, (3.14.3)

. (3.14.6)

Будем иметь

.

Следствие 3 доказано.