2º. Координатный способ задания движения твердого тела

Обозначим — орты абсолютной системы , — координаты вектора  в абсолютной системе, — координаты вектора  . Тогда после умножения (3.2.2) скалярно на орты получим

,

, (3.2.3)

.

Обозначим в (3.2.3) , ,  , — коэффициенты при .

,

,

.

Обозначим матрицу коэффициентов

.

Определение 2

Матрица называется матрицей перехода от связанной системы координат к абсолютной, или иначе, матрицей ориентации твердого тела в абсолютном пространстве.

Из соотношений (3.2.3) делаем следующий вывод.

Если задано движение полюса связанной системы координат тремя дважды непрерывно дифференцируемыми координатными функциями и задана матрица ориентации твердого тела в абсолютном пространстве, то движение твердого тела определяется соотношениями (3.2.3):

,

, (3.2.3)

.

Выражения (3.2.3) — это координатный способ задания движения твердого тела.

3º. Матричная и векторно-матричная формы записи задания движения твердого тела

3.1. Матричная форма записи задания движения твердого тела

Перепишем соотношения (3.2.3) в матричном виде

. (3.2.4)

Выражение (3.2.4) — это матричная форма записи задания движения твердого тела.

Согласно этой форме необходимо задать столбцовую матрицу и матрицу .

Элементы матриц должны быть дважды непрерывно дифференцируемыми функциями времени . И тогда вектор , вычисляемый по формуле (3.2.4)

, (3.2.4)

определяет движение твердого тела.

В (3.2.4) вектор является постоянным. Этим вектором задаются геометрические характеристики выбранной точки твердого тела.

Таковыми являются координаты указанной точки в той связанной системе координат, которая служит основой для описания ориентации тела.

3.2. Векторно-матричная форма записи задания движения твердого тела

Обозначим через вектор

.

Под вектором будем понимать вектор с компонентами в абсолютном пространстве, которые задаются соотношениями

.

Начало вектора совпадает с полюсом связанной системы.

Тогда (3.2.4) можно записать в виде

. (3.2.5)

Выражение (3.2.5) — это векторно-матричная форма записи задания движения твердого тела.

§3. Матрица ориентации, ее геометрический смысл и основные свойства

Отметим основные свойства матрицы ориентации .

1. Твердое тело имеет бесчисленное множество матриц ориентации.

Это следует из того, что твердое тело имеет бесчисленное множество связанных систем координат.

2. Для каждой фиксированной связанной системы матрица — единственная.

3. Матрица не зависит от выбора полюса связанной системы.

4. Столбцами матрицы являются направляющие косинусы ортов связанной системы в абсолютной системе координат, а строками — координаты ортов абсолютной системы в связанной.

Поэтому матрицу называют также матрицей направляющих косинусов. Таков ее геометрический смысл.

5. Элементы 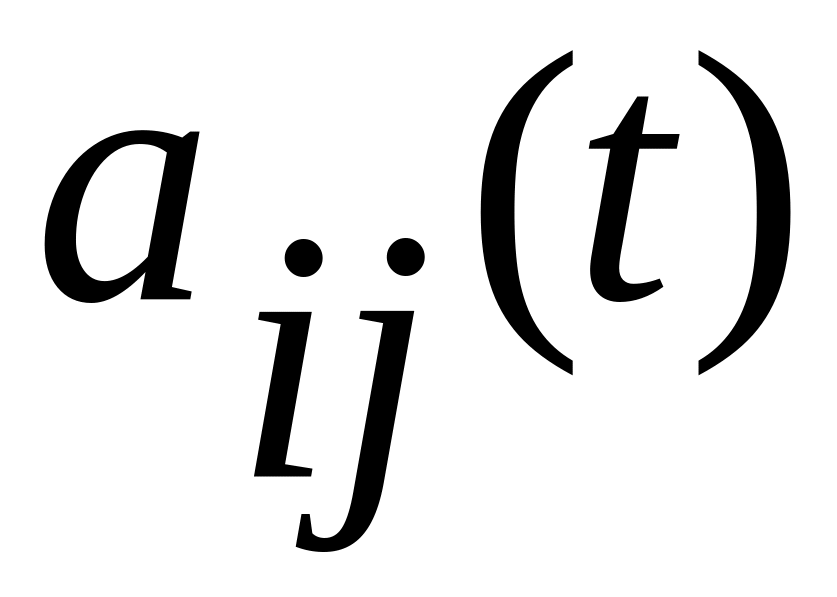матрицы на любых движениях твердого тела удовлетворяют следующим тождествам по времени :

(3.3.1)

6. Из векторных соотношений

получаем девять условий, связывающих элементы , , матрицы  , следующего типа:

(3.3.2)

7. Из соотношений (3.3.1) и (3.3.2) вытекает

, .

Здесь — обратная матрица, — транспонированная.

8. Тождества (3.3.1) означают, что на 9 элементов матрицы  наложено 6 ограничений (в любой момент времени ). Отсюда делаем вывод, что матрица  (в общем случае) может быть задана с помощью трех независимых переменных.

Пусть имеем две связанные системы координат и .

Обозначим:

— матрицу ориентации системы ,

— матрицу ориентации системы ,

— матрицу перехода от к .

Очевидно, что при любых матрица остается постоянной, поскольку ее элементами являются направляющие косинусы ортов системы (если смотреть по столбцам) в системе .

А так как орты любой связанной системы неподвижны в теле, то их направляющие косинусы остаются постоянными в любой связанной системе координат.

Для любой точки с координатами в абсолютном пространстве можно записать:

, . (3.3.3)

Здесь – координаты точки в системе  , .

Поскольку координаты точки в системе  связаны с ее координатами в системе  через матрицу соотношением

, (3.3.4)

то, подставляя (3.3.4) в (3.3.3), получим

. (3.3.5)

Равенства (3.3.5) справедливы для любой точки  , т.е. для любых значений координат .

А тогда из (3.3.5) следует, что в любой момент времени будет выполняться

. (3.3.6)

Формула (3.3.6) устанавливает связь двух матриц ориентации твердого тела в любой момент времени .