2.6 Дробовий факторний експеримент

Експеримент, в якому проводяться 2^k дослідів, де k – кількість вхідних факторів, називається повним факторним експериментом (ПФЕ).

В теорії планування експерименту існують методи побудови частин планів ПФЕ, яким притаманні основні властивості ортогонального планування. Такі експерименти називають дробовими (ДФЕ).

ДФЕ є частиною ПФЕ. Якщо проводиться половина ПФЕ (замість N_k=2^k дослідів проводиться половина, тобто ½N_k або 2^к-1), то експеримент називається півреплікою ПФЕ; якщо проводиться ¼N_k=2^к-2 дослідів, то експеримент називається четвертю репліки ПФЕ 2^к і т.д.

Будь-які дробові репліки повинні мати властивості ортогональності, нормування та балансу (див. pозділ 2.5).

Дробові репліки значно зменшують кількість необхідних дослідів – наборів різних комбінацій факторів, - зокрема кількість дослідів можна зробити рівною кількості факторів.

План, в якому кількість дослідів дорівнює кількості коефіцієнтів регресії bі, називається насиченим.

Дробові репліки зручні для побудови лінійних моделей систем з великою кількістю вхідних факторів (при цьому апріорі повинно бути відомо, що ефекти взаємодії проявляються слабо), а також для дослідження багатофакторного простору в першому наближенні, коли поверхня відгуку мало відрізняється від гіперповерхні, тобто в області, де допустима лінеаризація.

2.7 Врахування нелінійності типу квадратів факторів

У тих випадках, коли поверхня відгуку має вигляд горба (або впадини), тобто коли функція відгуку має екстремум, рівняння моделі дещо ускладнюється – в ньому з`являються квадрати рівнів факторів:

(2.19)

У випадку, якщо рівняння (2.17) незадовільно описує досліджувану систему і є потреба перейти до рівняння (2.19), весь експеримент не повторюють з самого початку, а лиш доповнюють план експерименту новими точками: одна з них знаходиться в центрі плану (х_і=0), а інші, що називаються зірковими точками, знаходяться на осях х_і на певній відстані  від центру плану. На рис.2.4 показано розміщення точок такого експерименту для двох вхідних факторів (k=2). Зіркові точки відмічені кружками; величина  називається зірковим плечем.

Загальна кількість дослідів збільшується від N=2^к, до N=2^k+2k+1, якщо система описується рівнянням (2.19); k – кількість вхідних факторів.

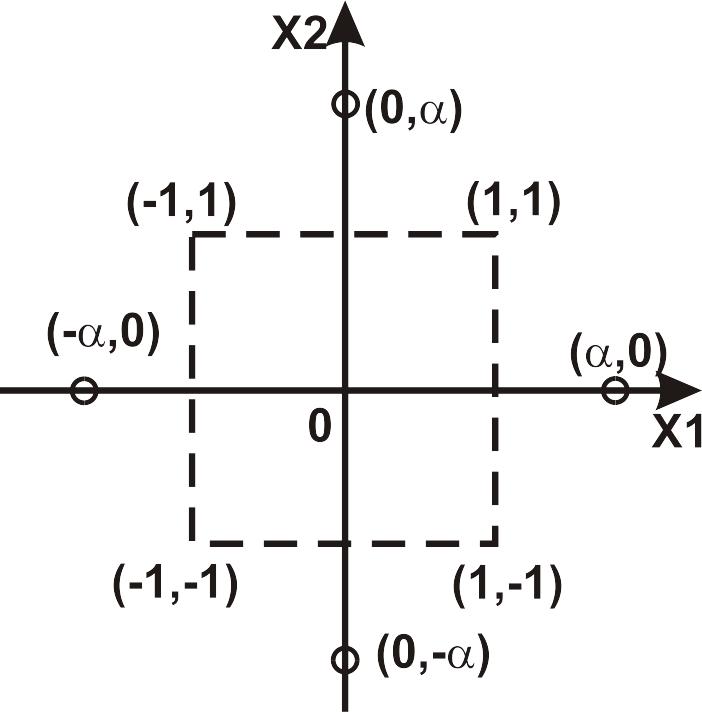
Рисунок 2.4 – Взаєморозміщення точок двофакторного експерименту і зіркових точок

Планування такого експерименту та обробка його результатів найкоротше викладені в роботі [2], а цікавий приклад наведений у додатку А.

2.8 Планування експерименту при пошуку оптимуму

Напевне, в більшості випадків потрібно визначить такі значення факторів, які забезпечують досягнення максимуму відгуку у. На значення факторів можуть накладатись певні обмеження.

Експерименти, що проводяться з метою досягнення максимуму чи мінімуму відгуку у, називаються екстремальними або оптимізаційними.

На першому етапі проводять багатофакторний експеримент в довільній області _ факторного простору.

На другому і наступних етапах здійснюється рух в точку оптимуму (екстремуму) одним із методів: градієнтним, найшвидшого спуску (підйому), випадкового (статистичного) пошуку і т.д. Одним із найчастіше використовуваних методів є видозмінений метод градієнта, який називається методом крутого сходження. На прикладі двофакторного експерименту розглянемо рух до точки у=у_mах за допомогою цього методу.

Стратегію дослідження екстремуму пояснює рис. 2.5.

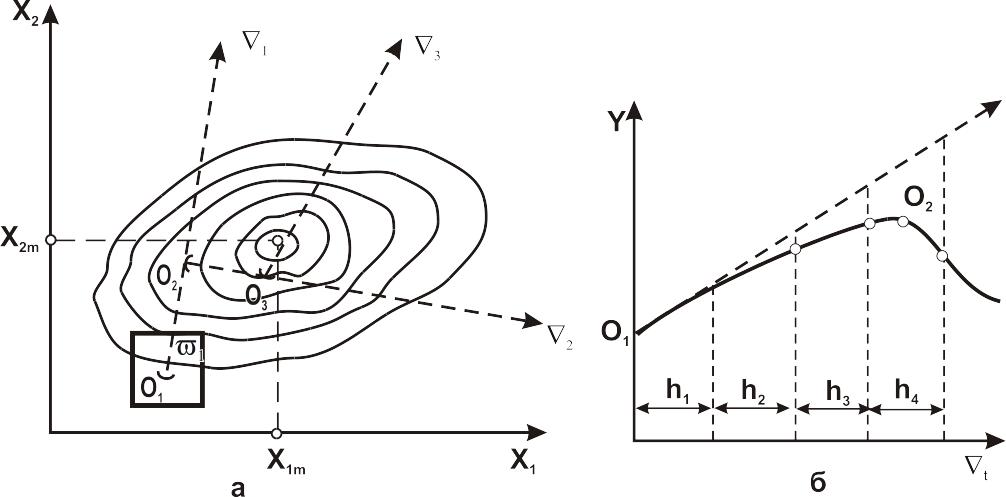
а – поверхня відгуку; б – переріз поверхні відгуку площиною, що проходить через вектор ₁.

Рисунок 2.5 – Геометрична інтерпретація метода крутого сходження

На рис.2.5, а побудовані криві однакового рівня відгуку у=const. Після проведення експерименту в області _ отримуємо рівняння регресії, наприклад, у вигляді

y = __x₁ + _ x₂. (2.20)

З цього рівняння визначаємо напрям градієнта:

(2.21)

Будемо рухатись в напрямку вектора _, починаючи з точки О₁ (центр області _).

Для більшої наочності перетнемо поверхню відгуку вертикальною площиною, що проходить через вектор _, і отримаємо криву, зображену на рис. 8.1б. З цього рисунка видно, що через декілька кроків h, в процесі яких вимірюється лиш відгук у (а нове значення градієнта не обчислюється), ми прийдемо в точку О₂, після якої значення відгуку почне зменшуватися і в якій відгук у досягне найбільшого значення для даного напрямку.

Точка О₂ стає центром плану для другої серії дослідів в області _ (на рисунку не виділена); далі обчислюються нові значення коефіцієнтів b_і та новий напрям градієнта _. По напрямку _ дійдемо до точки О₃, в якій поставимо третю серію дослідів і обчислимо напрям градієнта _, який і виводить нас в область максимуму. Тут завершується круте сходження і починається детальне дослідження відгуку в околицях максимуму. Це здійснюють за допомогою планування другого порядку (з врахуванням нелінійності типу квадратів факторів).

Примітка. Оптимізація системи за наявності ряду обмежень (умов) може здійснюватись також симплекс-методом [2, 4].