Расчетная таблица

Номер предприятия	Выпуск продукции, тыс. ед. х	Затраты на производство, млн. руб. у
1 2 3 4 5 6 7	1 2 4 3 5 3 4	30 70 150 100 170 100 150	30 140 600 300 850 300 600	1 4 16 9 25 9 16	900 4900 22500 10000 28900 10000 22500	31,1 67,9 141,6 104,7 178,4 104,7 141,6
Итого	22	770	2820	80	98890	770

Система нормальных уравнений будет иметь вид:

Решив ее, получим:

.

Уравнение регрессии примет вид:

Коэффициент регрессии при этом отражает, что с увеличением выпуска продукции на 1 тыс. ед. издержки возрастают в среднем на 36,84 млн. руб., то есть дополнительный прирост продукции на одну единицу своего измерения потребует увеличения затрат на производство продукции в среднем на 36,84 млн. руб.

Подставив в уравнение значения х, найдем теоретические значения у. В данном случае параметр не имеет экономического смысла. В рассматриваемом примере также имеем следующие значения средних квадратических отклонений в ряду х и у:

;

;

.

Ниже представлен расчет относительного показателя вариации: коэффициент вариации:

;

.

То, что ‹ 0, соответствует опережению изменения результата над изменением фактора: .

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции для линейной регрессии (-1 ≤ ≤ 1):

,

где - среднее квадратическое отклонение в ряду x,

- среднее квадратическое отклонение в ряду y.

Линейный коэффициент корреляции как измеритель тесноты линейной связи признаков связан не только с коэффициентом регрессии b, но и с коэффициентом эластичности, который является показателем силы связи, выраженным в процентах.

Коэффициент эластичности отражает, на сколько процентов изменится значение y при изменение значения фактора на 1%. Коэффициент эластичности рассчитывается как .

Обобщающий (средний) коэффициент эластичности рассчитывается для среднего значения :

и показывает, на сколько процентов изменится y относительно своего среднего уровня при росте x на 1% относительно своего среднего уровня.

Точечный коэффициент эластичности рассчитывается для конкретного значения x=x₀:

и показывает, на сколько процентов изменится y относительно своего уровня y(x₀) при увеличении на 1% от уровня x₀.

На основе данных примера рассчитаем коэффициент корреляции и средний коэффициент эластичности.

.

Полученный показатель близок к единице, следовательно между х и у связь весьма сильная, кроме того, так как полученное значение больше 0, то связь между х и у прямая.

Средний коэффициент эластичности при значении х равном 3,14 составит:

. Показатель при расчете сразу получается в процентах, умножать на 100% не нужно.

Средний коэффициент эластичности отражает, что с ростом средней величины факторного признака х на 1% среднее значение результативного признака возрастает в среднем на 1,053%.

Для оценки качества подбора линейной функции рассчитывается коэффициент детерминации. Коэффициент детерминации – это квадрат линейного коэффициента парной корреляции; он характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака:

,

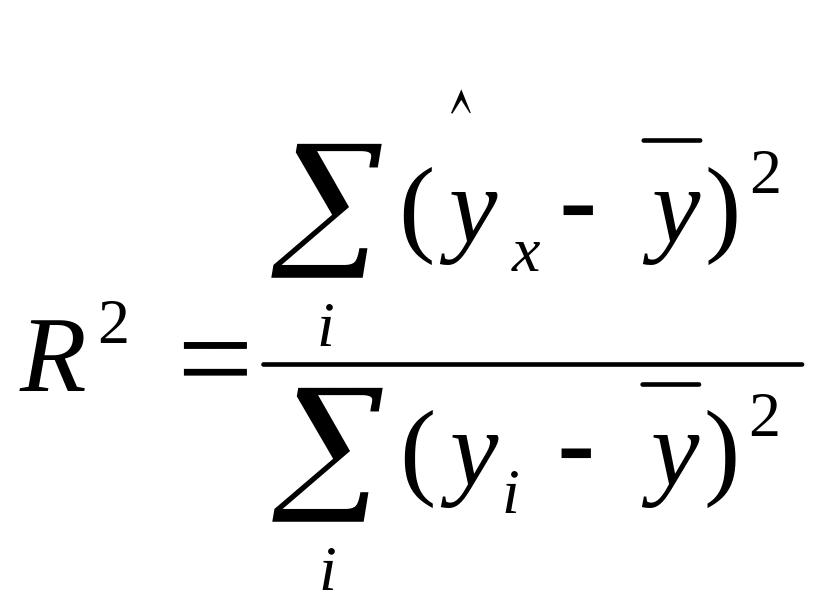где - сумма квадратов отклонений, обусловленная регрессией

(факторная);

- общая сумма квадратов отклонений.

Чем больше доля объясненной вариации, тем соответственно меньше роль прочих факторов и, следовательно, линейная модель хорошо аппроксимирует исходные данные, и ею можно воспользоваться для прогноза значений результативного признака. Иначе, чем ближе коэффициент детерминации к 1, тем в большей степени уравнение регрессии пригодно для прогнозирования.

После того как уравнение линейной регрессии найдено, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.

Проверка значимости уравнения регрессии осуществляется путем расчета F-критерия Фишера. F-тест состоит в проверке гипотезы Н₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Непосредственному расчету F-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений на две части: объясненную (факторную) и остаточную:

,

где - остаточная сумма квадратов отклонений.

Любая сумма квадратов отклонений связана с числом степеней свободы df, т.е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности n и с числом определяемых по ней констант. Применительно к исследуемой проблеме число степеней свободы должны показать, сколько независимых отклонений из n возможных требуется для образования данной суммы квадратов. Так, для общей суммы квадратов необходимо (n-1) независимых отклонений, ибо по совокупности из n единиц после расчета среднего уровня свободно варьируют лишь (n-1) число отклонений. Например, имеем ряд значений у: 1, 2, 3, 4, 5.

, и тогда n отклонений от среднего составят: -2; -1; 0; 1; 2. Поскольку сумма отклонений равна нулю ( ), то свободно варьируют лишь четыре отклонения, а пятое отклонение может быть определено, если четыре предыдущие известны.

При расчете объясненной, или факторной, суммы квадратов используются теоретические (расчетные) значения результативного признака, найденные по линии регрессии. При заданном объеме наблюдений по х и у факторная сумма квадратов при линейной регрессии зависит только от одной константы коэффициента регрессии b, то данная сумма квадратов имеет одну степень свободы.

Существует равенство между числом степеней свободы общей, факторной и остаточной суммами квадратов. Число степеней свободы остаточной суммы квадратов при линейной регрессии составляет n-2. Число степеней свободы для общей суммы квадратов определяется числом единиц, и поскольку мы используем среднюю вычисленную по данным выборки, то теряем одну степень свободы, т.е. df_общ = n – 1.

Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений или дисперсию на одну степень свободы:

; ; .

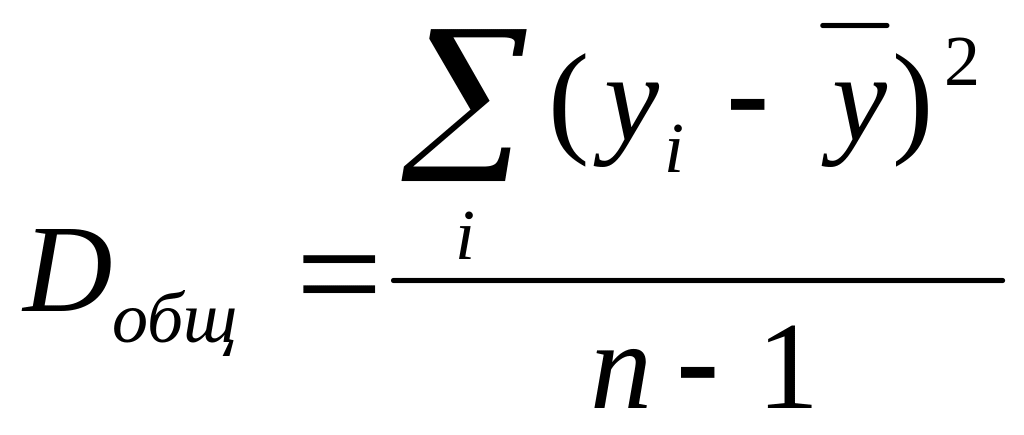Определение дисперсии на одну степень свободы приводит дисперсии к сравниваемому виду. Сопоставляя факторную и остаточную дисперсии на одну степень свободы, получим величину F-отношения, т.е. критерий F:

.

При линейной связи возможно использование формул:

или ,

где m – число параметров в уравнении регрессии;

(m-1) – число степеней свободы для факторной дисперсии;

n – число наблюдений;

(n-m) – число степеней свободы для остаточной дисперсии;

k – количество коэффициентов регрессии в уравнении регрессии.

Вместо числа параметров уравнения регрессии m можно использовать число коэффициентов регрессии k, которое на единицу меньше m, т.е. k=(m−1).

Вычисленное значение F-отношения признается достоверным (отличным от единицы), если оно больше табличного значения F-критерия. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи:

F_табл‹ F_факт, гипотеза Н₀ отклоняется.

F_табл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы ( ) и уровне значимости , который принимается равным 0,05 или 0,01.

Если же величина F окажется меньше табличной, то вероятность нулевой гипотезы выше заданного уровня и она не может быть отклонена без риска сделать неправильный вывод о наличии связи.

Продолжая рассмотрение примера, рассчитаем коэффициент детерминации и F-критерий Фишера.

− высокое значение коэффициент детерминации говорит о пригодности уравнения регрессии для прогнозирования.

В таблицу дисперсионного анализа подставим значения сумм квадратов отклонений.

Таблица 1.2

Расчетная таблица для определения общей суммы квадратов отклонений

Затраты на производство, млн. руб. у
30	-80	6400
70	-40	1600
150	40	1600
100	-10	100
170	60	3600
100	-10	100
150	40	1600
	×	15000

Таблица 1.3