Мода и медиана. Моменты случайных величин. Асимметрия и эксцесс. Квантили

Модой д. с. в. X называется ее значение, принимаемое с наибольшей вероятностью по сравнению с двумя соседними значениями, обознача- ется через М Х. Для н.с. в. М Х — точка максимума (локального)

ПЛОТНОСТИ f (x).

Если мода единственна, то распределение с. в. называется унимо- дальным, в противном случае — полимодалъным (рис. 23).

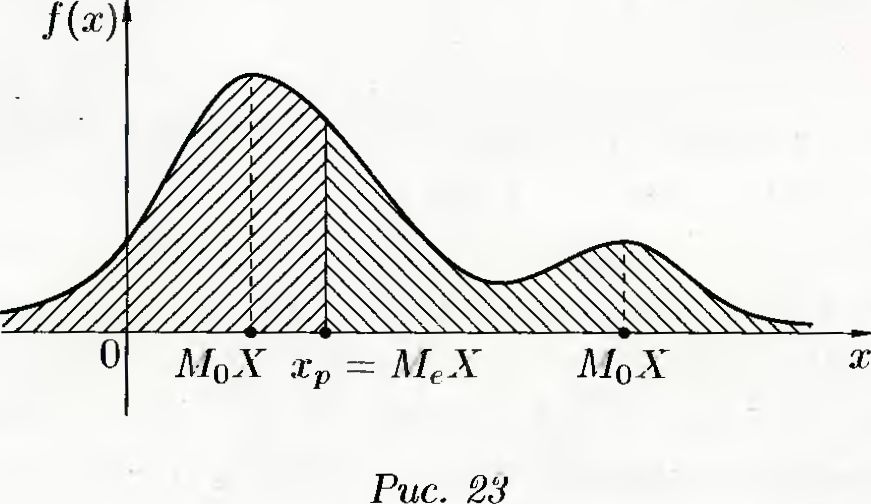
Медианой М Х н.с.в. X называется такое ее значение x , для ко- торого

Р{Х < х } = Р{Х > х } = , (2.19)

т. е. одинаково вероятно, окажется ли с. в. X меньше х или больше х (рис. 23).

С помощью функции распределения F(х) равенство (2.19) можно записать в виде Р(М Х) = 1 — f(М Х). Отсюда F(М Х) = .

Для д. с. в. медиана обычно не определяется.

Математическое ожидание и дисперсия являются частными случа- ями следующих более общих понятий - моментов с. в.

Начальным моментом порядка к с. в. X называется м. о. к-й сте- пени этой величины, обозначается через .

Таким образом, по определению

= М(Х ).

Для д. с. в. начальный момент выражается суммой:

а для н. с. в. — интегралом:

.

В частности, = МX, т. е. начальный момент 1-го порядка есть м. о.

Центральным моментом порядка к с. в. X называется м. о. вели- чины (X — МХ) , обозначается через .

Таким образом, по определению

= М(Х — МХ)

В частности, = DХ, т. е. центральный момент 2-го порядка есть дисперсия; = М(X — МХ) = 0 (см. свойство 4 м. о.).

Для д. с. в.:

а для н. с. в.:

Центральные моменты могут быть выражены через начальные моменты. Так, (действительно: ; и т.д.

Среди моментов высших порядков особое значение имеют цен- тральные моменты 3-го и 4-го порядков, называемых соответственно коэффициентами асимметрии и эксцесса.

Коэффициентом, асимметрии («скошенности») А с. в. X называ- ется величина

Если А > 0, то кривая распределения более полога справа от Х (рис. 24).

Если А < 0, то кривая распределения более полога слева от Х (рис. 25).

Коэффгициентом эксцесса («островершинности») Е с. в. X назы- вается величина

Рис. 25

Величина Е характеризует островершинность или плосковершин- ность распределения. Для нормального закона распределения (см. п. 2.7) А = 0 и Е = 0; остальные распределения сравниваются с нор- мальным: если Е > 0 - более островершинные, а распределения «плос- ковершинные» имеют Е < 0 (рис. 26).

Кроме рассмотренных выше числовых характеристик с. в., в при- ложениях используются так называемые квантили.

Квантилъю уровня р с. в. X называется решение уравнения

,

где р — некоторое число, 0 < р < 1.

Квантили и имеют свои названия: нижняя квартиль, медиана ( Х = ), верхняя квартиль соответственно. Они делят числовую прямую на 4 части, вероятности попадания в которые равны 0,25 (рис. 27).

Производящая функция

Нахождение важнейших числовых характеристик д. с. в. с целыми неотрицательными значениями удобно производить с помощью произ- водящих функций.

Пусть д. с. в. X принимает значения 0,1,2,..., k,... с вероятностя- ми

Производящей функцией для д. с. в. X называется функция вида

(2.20)

где z произвольный параметр, 0 < z 1.

Отметим, что коэффициентами степенного ряда (2.20) являются вероятности закона распределения д. с. в. X.

Дифференцируя по z производящую функцию, получим

Тогда

т. е.

(2.21)

Взяв вторую производную функции и положив в ней z = 1, полу- чим:

Где и - начальные моменты соответственно 2-го и 1-го порядков

Тогда т.е.

. (2.22)

Полученные формулы (2.21) и (2.22) используются для нахождения м. о. и дисперсии рассматриваемого распределения.

Пример 2.6. Найти дисперсию с. в. X — числа попаданий в упражне- нии 1 (п. 2.5).

X	0	1	2	3
р	0,01	0,027	0,243	0,729

Ряд распределения с. в. X:

Найдем DX, используя формулу (2.22). Производящая функция = = 0,01 + 0,027z + 0,243z + 0,729z . Тогда = 0,027 +0,486z+ 2187z . Полагая z = 1, находим (1) = 2,7 = МХ (упражнение 1 из п. 2.5). . Поэтому (1) = 4,46 и DX = 4,86 + 2,7 — (2,7) = = 0,27 (формула (2.22)).

Аналогично решаем во втором случае, когда вероятности при раз- ных выстрелах различны (п. 1.20, пример 1.31). (z) = 0,006 + 0,092z + + 0,398z + 0,504z . = 0,092 + 0,796z + 1,512z , = 2,4 = МХ.

(z) = 0,796 + 3,024z, "(1) = 3.82. Поэтому DХ = 3,82 + 2,4 — (2,4) = = 0,46.

8