Показательный закон распределения

Непрерывная случайная величина X имеет показательный (или экспоненциальный) закон распределения, если ее плотность вероятно- сти имеет вид

(2.35)

где > 0 параметр распределения.

График плотности f(х) приведен на рис. 32.

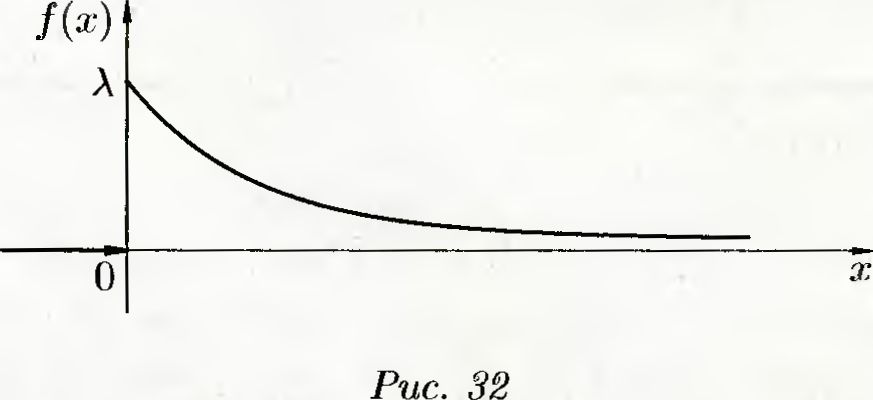
Функция распределения показательного распределения имеет вид

(2.36)

График F(x) представлен на рис. 33.

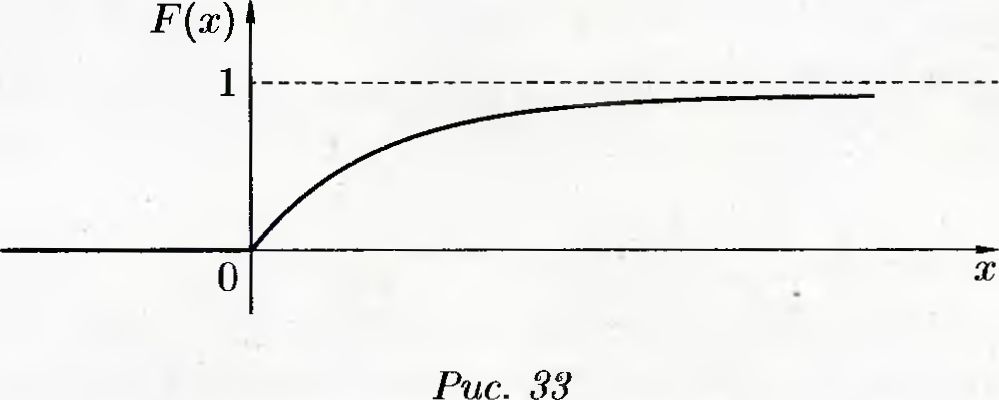
Найдем математическое ожидание и дисперсию показательного распределения:

=[интегрируем по частям] =

=

=[дважды интегрируем по частям]=

=

₌

Таким образом,

, (2.37)

Найдем вероятность попадания случайной величины X, распределен- ной по показательному закону, в интервал (а,b). Используя форму- лу (2.2) и формулу (2.36), получаем

Пример 2.12. Случайная величина Т – время работы радиолампы имеет показательное распределение. Найти вероятность того, что лам- па проработает не менее 800 часов, если среднее время работы радио лампы 400 часов.

О МТ = 400, значит (формула (2.37)), Искомая вероятность

Показательное распределение используется в приложениях теории вероятностей, особенно в теории массового обслуживания (ТМО), в фи- зике, в теории надежности. Оно используется для описания распреде- ления случайной величины вида: длительность работы прибора до пер- вого отказа, длительность времени обслуживания в системе массового обслуживания и т.д.

Рассмотрим, например, н. с. в. Т — длительность безотказной ра- боты прибора. Функция распределения с. в. Т, т. е. , определяет вероятность отказа за время длительностью t. И, значит, вероятность безотказной работы за время t равна . Функция R(t) называется функцией надежности.

Случайная величина Т часто имеет показательное распределение. Ее функция распределения имеет вид (формула (2.36)). В этом случае функция надежности имеет вид т.е. ,где — интенсивность отказов, т. е. среднее число отказов в единицу времени.

Показательный закон — единственный из законов распределения, который обладает свойством «отсутствия последствия» (т. е. если про- межуток времени Т уже длился некоторое время , то показатель- ный закон распределения остается таким же и для оставшейся части промежутка).

Нормальный закон распределения

Нормальный закон («закон Гаусса») играет исключительную роль в теории вероятностей. Главная особенность закона Гаусса состоит в том, что он является предельным законом, к которому приближаются, при определенных условиях, другие законы распределения. Нормаль- ный закон наиболее часто встречается на практике.

Непрерывная с. в. X распределена по нормальному закону с пара- метрами а и > 0, если ее плотность распределения имеет вид

(2.38)

Тот факт, что с. в. X имеет нормальное (или гауссовское) распреде- ление с параметрами а и а, сокращенно записывается так:

Убедимся, что f(x) – это функция плотности. Очевидно, f(x) > 0.

Проверим выполнение условия нормировки . Имеем:

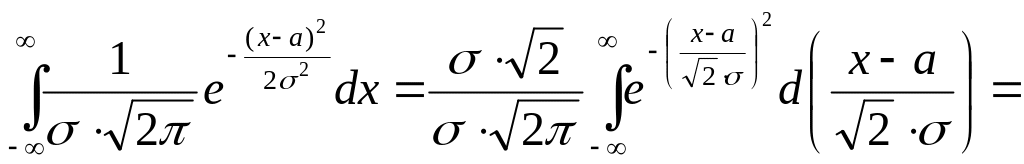
Здесь применили подстановку и использовали «интеграл Пуассона»

(2.39)

Из равенства (2.39) следует:

(2.40)

Функция распределения н. с. в. имеет вид

(2.41)

Если а = 0 и = 1, то нормальное распределение с такими параме- трами называется стандартным. Плотность стандартной случайной величины имеет вид

С ней мы уже встречались в п. 1.21, формула (1.37).

Функция распределения с. в.X~N(0,1) имеет вид

и называется, как мы уже знаем (п. 1.21, формула (1.42)), функци- ей Лапласа. Она связана с нормированной функцией Лапласа (п. 1.21, формула (1.40)), как мы уже знаем (формула (1.43) п. 1.21), равенством

(2.42)

Действительно,

=

(см. (2.40)).

Установим смысл параметров а и нормального распределения. Для этого найдем математическое ожидание и дисперсию с. в. X ~ ~ N(a, ).

=[подстановка ]=

=

т. е. МX = а. Первый интеграл равен нулю, так как подинтегральная функция нечетная, а пределы интегрирования симметричны относи- тельно нуля, а второй интеграл равен (см. равенство (2.39)). Таким образом, параметр а — математическое ожидание.

При нахождении дисперсии с. в. X ~ N (а, ) снова сделаем подстановку и применим метод интегрирования по частям:

Таким образом, , а — среднее квадратичное отклонение.

Можно показать, что для с. в. : , .

Исследуем дифференциальную функцию (2.38) нормального за- кона:

1. f(x) > 0 при любом ; график функции расположен

выше оси Оx.

2. Ось Оx служит асимптотой графика функции f(x), так как

3. Функция f(x) имеет один максимум при x = а, равный . Действительно,

Отсюда f(x) = 0 при х = а, при этом: если x < а, то f’(x) > 0, a если x > а, то f’(x)< 0. Это и означает, что x = а точка максимума

Основные законы распределения случайных величин. Биномиальный закон распределения 3

Распределение Пуассона 7

Геометрическое распределение 12

Гипергеометрический закон распределения 19

Равномерный закон распределения 22

Показательный закон распределения 30

Нормальный закон распределения 36

и

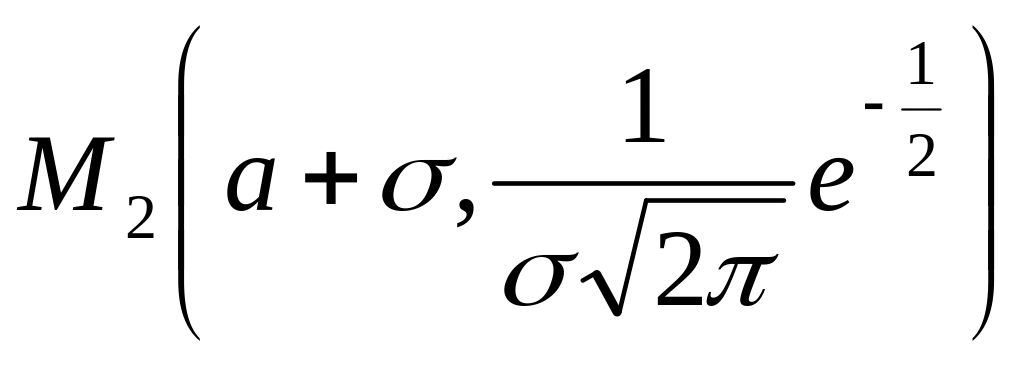
являются точками перегиба графика функции f(x).

Пользуясь результатами исследования, строим график плотности распределения вероятности нормального закона — кривую распреде- ления, называемую нормальной кривой, или кривой Гаусса (рис. 34).

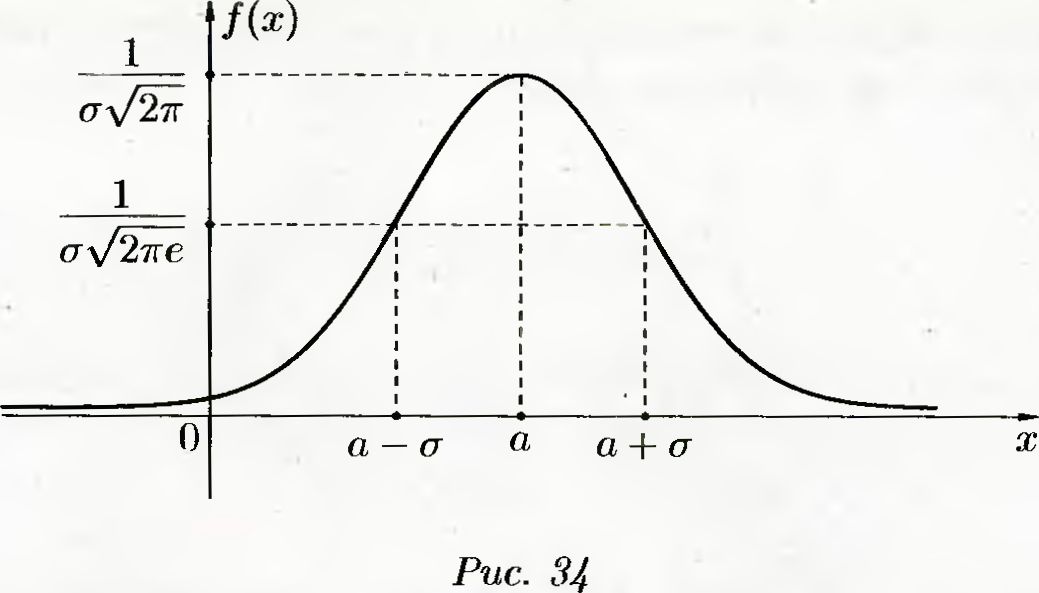
Как влияет изменение параметров a и на форму кривой Гаус- са? Очевидно, что изменение а не изменяет форму нормальной кривой (графики функции f(x) и f(x — а) имеют одинаковую форму; график f(x — а) получается из графика функции f(x) путем сдвига последнего на а единиц вправо, если а > 0, и влево, если а < 0). С изменением о максимальная ордината точки кривой изменяется. Так как площадь, ограниченная кривой распределения, равна единице при любом значе- нии , то с возрастанием кривая Гаусса становится более пологой, растягивается вдоль оси Ох …

На рис. 35 изображены нормальные кривые при различных значе- ниях ( ) и некотором значении а (одинаковом для всех трех кривых).

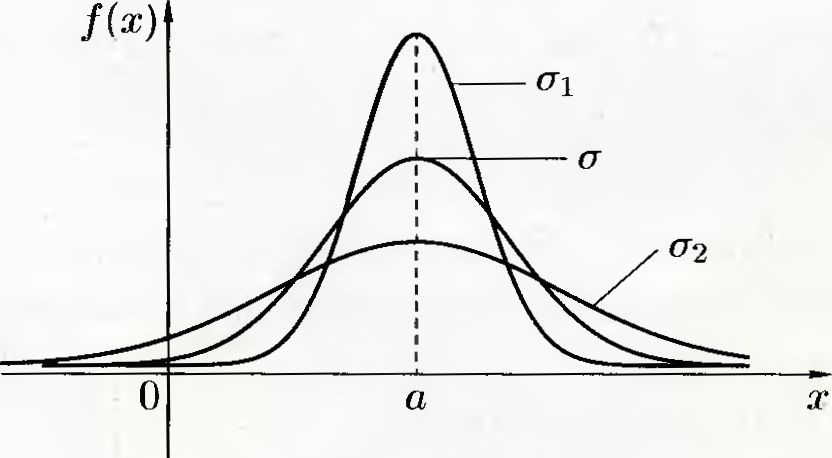
Рис. 35

Нормальному закону подчиняются ошибки измерений, величины износа деталей в механизмах, рост человека, ошибки стрельбы, вес клубней картофеля, величина шума в радиоприемном устройстве, ко- лебания курса акций и т. д.

Найдем вероятность попадания с. в. X ~ N(a, ) на заданный уча- сток ( ). Как было показано,

(п. 2.4, формула (2.8)). В случае нормального распределения

^ (х — а)2

Основные законы распределения случайных величин. Биномиальный закон распределения 3

Распределение Пуассона 7

Геометрическое распределение 12

Гипергеометрический закон распределения 19

Равномерный закон распределения 22

Показательный закон распределения 30

Нормальный закон распределения 36

получаем

. (2.43)

Через функцию Лапласа выражается и функция распределения F(х) нормально распределенной с. в. X.

т. е.

(2.44)

Здесь воспользуемся формулой (2.43), нечетностью функции и тем, что , действительно

Если функция Лапласа (или «интеграл вероятностей») есть

то

(2.45)

(непосредственно вытекает из равенств (2.42)) и (2.44)).

Равенство (2.43) можно переписать и так:

(2.46)

На практике часто приходиться вычислять вероятность попада- ния нормально распределенной случайной величины в интервал, сим- метричный относительно центра рассеяния а. Пусть таким интер- валом будет (а-l, a+l) длины 2l. Тогда т.е.

. (2.47)

Полагая в равенстве (2.47) , получим (3).

По таблице значений для находим: . Следова-

тельно, 0.9973, т. е. отклонение с. в. X от своего математического ожидания меньше, чем З — почти достоверное собы- тие.

Важный вывод: практически достоверно, что с. в. X ~ N(a, ) при- нимает свои значения в промежутке ( ). Это утверждение называется «правилом трех сигм».

Пример 2.13. При измерении детали получаются случайные ошибки, подчиненные нормальному закону с параметром = 10 мм. Произво- дится 3 независимых измерения детали. Найти вероятность того, что ошибка хотя бы одного измерения не превосходит по модулю 2 мм.

О По формуле (2.47) находим:

Вероятность того, что эта ошибка (погрешность) превышает 2 мм в одном опыте (измерении), равна

По теореме умножения вероятность того, что во всех трех опытах ошиб- ка измерения превышает 2 мм. равна . Следовательно, искомая вероятность равна 1 — 0,5958 = 0,4042. •

Упражнения

Известно, что с. в. X ~ N(3,2). Найти

Р{—3 < X < 5}, Р{Х 4}, Р{|Х-3|<6}.

Нормально распределенная с. в. X задана плотностью вероятно- стей

Найти: а) вероятность попадания с. в. в интервал (1,3); б) симмет- ричный относительно математического ожидания интервал, в ко- торый с вероятностью 0,8926 попадет с. в. X в результате опыта; в) и . Построить нормальную кривую f(x).

1