Основные законы распределения случайных величин. Биномиальный закон распределения
Среди законов распределения д. с. в. наиболее распространенным является биномиальное распределение, с которым мы уже встречались (п. 1.20).
Дискретная с. в. X имеет биномиальное распределение (или рас- пределена по биномиальному закону), если она принимает значения 0,1,2,3,, п, с вероятностями:
(2.23)
где 0 < р < 1, q = 1 — р, m = 0,1,…, n.
Случайная величина X, распределенная по биномиальному закону, является числом успехов с вероятностью p в схеме Бернулли проведения n независимых опытов.
Если
требуется вычислить вероятность «не
менее m
успехов в n
независимых
опытах», т. е. Р{
}, то имеем : Pm
=
Вероятность
бывает удобно находить через вероятность
противоположного события:
;
та из двух формул лучше, где меньше
слагаемых.
Ряд распределения д. с. в. X, имеющей биномиальное распределе- ние, имеет вид:
X = m |
0 |
1 |
2 |
… |
m |
… |
n |
|
|
|
|
… |
|
… |
|
Контроль:
Функция распределения с. в. X, распределенной по биномиальному закону, имеет вид:
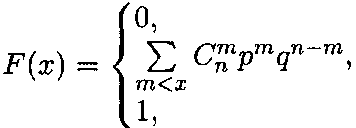
при
при n < х.
Основные законы распределения случайных величин. Биномиальный закон распределения 3
Распределение Пуассона 7
Геометрическое распределение 12
Гипергеометрический закон распределения 19
Равномерный закон распределения 22
Показательный закон распределения 30
Нормальный закон распределения 36
.
,т.е.
Тогда
,
Следовательно
(см. п. 2.6)
,
т.к.
,
.
Итак,
,
(2.24)
Эти формулы полезно знать.
Пример 2.7. По условию упражнения 1 из п. 2.5 найти МХ и РХ, где X — число попаданий в цель.
О
С. в. X имеет биномиальное распределение.
Здесь
,
,
По формулам (2.24) находим МХ и DX: МХ = 3 •
0,9 = 2,7,
DX = 3 • 0,9 • 0,1 = 0,27.
Распределение Пуассона
Дискретная случайная величина X имеет распределение Пуассона, если ее возможные значения: 0,1,2,...,m,... (счетное множество зна- чений), а соответствующие вероятности выражаются формулой Пуассона
(2.25)
где
,
а
–
параметр
Распределение
Пуассона является предельным для
биномиальною,
когда
и
так, что пр
= а
постоянно. Примерами слу-
чайных
величин, имеющих распределение Пуассона,
являются: число вызовов на телефонной
станции за время t;
число опечаток в большом
тексте;
число бракованных деталей в большой
партии; число
-частиц,
испускаемых радиоактивным источником,
и т.д. При этом считается, что события
появляются независимо друг от друга с
постоянной средней интенсивностью,
характеризующейся параметром а
= пр.
Случайная величина X, распределенная по закону Пуассона, имеет следующий ряд распределения
|
0 |
1 |
2 |
… |
m |
… |
|
|
|
|
… |
|
… |
Контроль: 
Найдем м. о. и дисперсию с. в. X, распределенной по закону Пуас- сона. Производящей функцией распределения Пуассона будет
т.е.
.
Тогда
,
Стало
быть,
,
Итак,
(2.26)
т. е. параметр о пуассоновского распределения равен одновременно м.о. и дисперсии с. в. X, имеющей это распределение. В этом состоит отличительная особенность изучаемого распределения, которая используется на практике (на основании опытных данных находят оценки для м. о. и дисперсии; если они близки между собой, то есть основание счиать, что с. в. распределена по закону Пуассона).
Пример 2.8. Вероятность попадания в цель при одном выстреле равна. 0,01. Какова вероятность того, что число попаданий при 200 выстрелах составит не менее 5 и не более 10?
О
Вероятность р = 0,01 очень мала, а число
выстрелов (опытов)
достаточно велико.
Поэтому искомую вероятность будем
находить,
используя формулу Пуассона.
С. в. X - число попаданий. Требу-
ется
найти Р{
}.
По теореме сложения вероятностей
. Имеем:
,
,
