2. Модели планирования вычислительного процесса

Для решения каждой задачи должен быть выделен определенный ресурс по объ­ему оперативной и внешней памяти, по времени работы процессора, времени ввода-вывода информации. Естественно, что ограничен­ность вычислительных ресурсов может не позволить решать вычис­лительные задачи параллельно во времени. Учитывая, что вычис­лительная система при однолинейном обслуживании зачастую мо­жет решать только одну задачу, необходимо составить план последовательного запуска задач. Процесс назначения порядка решения задач во времени называется планированием. Для многолинейной системы планирование предполагает распределение заявок как во времени, так и в пространстве по используемым ЭВМ. В качестве распределяемых ресурсов выступают машинное время процессоров, объемы оперативной памяти и внешних запоминающих устройств, время работы устройств ввода-вывода. Эти ресурсы могут быть реализованы, если вычислительная задача подготовлена к выполне­нию ее вычислительной системой. Подготовка вычислительной за­дачи к исполнению осуществляется управляющей программой, на­зываемой планировщиком. Планировщик обеспечивает ввод вычис­лительных задач в вычислительную систему с предварительным формированием определенных информационно-вычислительных работ на базе заявок вычислительных задач. При возникновении заявки на решение вычислительной задачи необходимо установить программу и набор данных, которые позволят сформировать ин­формационно-вычислительную работу по решению данной задачи. Одновременно следует установить потребность в ресурсах и вклю­чить сформированную информационно-вычислительную работу в список работ, готовых для последующего исполнения. В резуль­тате планирования по каждой задаче может быть сформирован ряд работ, выполнение которых возможно при реализации управля­ющей программы, называемой супервизором. Супервизор обеспечивает предоставление каждой сформированной работе определен­ного ресурса процессора и других устройств вычислительной системы. Супервизор действует по запросу, на который откликается программа управления работами и процессором. При управлении информационно-вычислительными работами супервизор непрерывно инициируется командами, которые задает планировщик. Планировщик в соответствии с планом организации вычислительного процесса из множества заявок на решение вычислительных задач выделяет наиболее приоритетную и требует обеспечения ее соответствующими ресурсами. Для этого он обращается к программе управления вводом и выводом, памятью и т. д. В целом функция планирования реализуется управляющими программами планиров­щика и супервизора. Критерии, используемые при планировании вычислительного процесса, могут выбираться в зависимости от требований к решаемым вычислительным задачам. Можно идти по пути уменьшения среднего времени решения задач в вычислитель­ной системе или увеличивать производительность. Возможны вари­анты, когда имеются ограничения на время решения конкретных задач, что особенно важно в системах управления в реальном масштабе времени.

Рассмотрим модель планирования вычислительного процесса. Будем считать, что в целом для ряда вычислительных задач необходимым является выполнение определенной номенклатуры типовых вычислительных работ J₁ — J_y, для которых необходимо предоставление ресурсов R­₁ — R_у. Связь между работами и ре­сурсами можно установить в виде матрицы трудоемкости работ. Элементами этой матрицы служат параметры _ij, которые в зависимости от характера требуемого ресурса имеют размерность числа единиц потребной памяти либо единиц времени, необхо­димых для выполнения соответствующей работы. Тогда вводимая матрица имеет вид

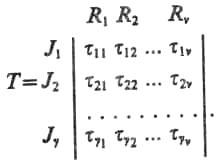
Имея данную матрицу, при составлении плана организации вычислительного процесса необходимо указать очередность выпол­нения работы отдельными устройствами вычислительной системы, т. е. последовательность использования ресурсов R₁ — R_ν.

Планирование вычислительного процесса осуществляется с це­лью составления последовательности, т. е. расписания выполнения информационно-вычислительных работ, производимых при реше­нии поступивших вычислительных задач. Учитывая, что при реше­нии вычислительной задачи используются разные устройства вычи­слительной системы (ВС), можно рассмотреть два крайних случая 1) порядок использования отдельных устройств ВС определяется поступившими вычислительными задачами; 2) порядок использования устройства ВС либо не известен, либо неодинаков для различных информационно-вычислительных работ. Этим крайним постанов­кам могут соответствовать и разные критерии эффективности со­ставления плана вычислительных работ. Для первой постановки в качестве критерия может быть выбран минимум суммарного времени решения вычислительных задач, для второй — можно из­брать в качестве критерия максимум загрузки устройств ВС. Плани­рование по минимуму суммарного времени решения вычислитель­ных задач возможно, если известна матрица трудоемкостей отдель­ных работ. Предполагая, что ресурсы вычислительной системы используются последовательно, и, выделяя типовую последователь­ность прохождения любой вычислительной задачи, можно получить эффективный алгоритм планирования на основе задачи Джонсона, которая относится к теории расписаний и широко используется в календарном планировании.

Планирование по критерию минимума времени обработки. При планировании вычислительного процесса необходимо учитывать следующие ограничения:

1) для любого устройства ВС (фазы обработки данных) каждая последующая работа не может начаться до окончания предыдущей;

2) каждое устройство на данной фазе может выполнять только одну информационно-вычислительную работу;

3) начавшаяся информационно-вычислительная работа не долж­на прерываться до полного ее завершения.

Если в процессе обработки выделить  фаз, на каждой из кото­рых используется одно вычислительное устройство, то решение данной задачи путем перебора требует рассмотрения (N!)^ вариан­тов, где N — число заявок на решение вычислительных задач в вы­числительной системе. Джонсоном получен эффективный алгоритм для =2, требующий перебора N(N+1)/2 вариантов. Частное реше­ние задачи Джонсона соответствует случаю =l. По сути, это однолинейная система обслуживания (S=1), в которой имеется очередь заявок. Требуется установить порядок выборки этих заявок Диспетчером Д₂ для обработки в ЭВМ. Критерием может быть минимум времени пребывания заявки в вычислительной системе, включая и время ожидания ее в очереди. Алгоритм выборки заявок из очереди по данному критерию соответствует их расположению в порядке убывания времени пребывания в вычислительной системе. Отметим, что решение задачи Джонсона при =1 имеет слабое фактическое применение для вычислительной системы. Обычно при обработке данных используется более одного устройства.

Отметим, что решение задачи Джонсона при >2 означает практически сведение этой задачи к двухфазной. В частности, для =3 получаем матрицу трудоемкостей, содержащую три столбца. Эту матрицу преобразуем в двухстолбцовую матрицу путем попарного сложения элементов трудоемкостей первого и второго, второго и третьего столбцов. Если ограничения, указанные Джонсоном, не выполняются, то точного решения задачи планиро­вания вычислительного процесса не имеется, и переходят к эв­ристическим алгоритмам планирования информационно-вычис­лительных работ. В основе эвристических алгоритмов лежит выделение фазы работ с наибольшей суммарной продолжитель­ностью. Данная фаза является приоритетной при запуске работ, которые располагаются в порядке убывания величин трудоем­костей их выполнения. Оценка эффективности эвристических методов планирования осуществляется по степени близости суммарного времени выполнения работ к минимально возможному времени.

Планирование по критерию максимума загрузки средств обработ­ки. Если последовательность использования вычислительных устройств в системе при решении задач неизвестна, то планирование ведут на основе критерия максимальной загрузки устройств. В этом случае из J₁...J_ отбирается совокупность работ, которые могут выполняться совместно на базе имеющихся ресурсов. По мере окончания хотя бы одной работы из этой совокупности выполнения заеняется одной из работ, находящихся в ожидании. Для определения составов совокупностей работ преобразуем матрицу трудоемкостей в матрицу загрузки устройств. Введенные ранее ресурсы R₁...R_ принадлежат некоторым устройствам У₁...У_. Тогда матрица загрузки может быть представлена в виде

где элемент матрицы З_ij показывает загрузку j-гo устройства i-й работой; ; — потребность i-й работы в использовании j-гo ресурса. В каждой строке матрицы выделим элемент З_ij, с наибольшим значением.

Тогда значение j определит номер потока, к которому будет отнесена работа, соответствующая данной строке матрицы. Число потоков будет равно числу устройств, т. е. . Если в первой строке наибольшее значение имеет элемент З₁₂, то работу J₂, относим к потоку П₂. Соответственно если во второй строке наибольшее значение имеет элемент З_2, то работу J₂ относим к потоку П_. При разбиении работ на потоки примем ограничение, что каждая из них может быть отнесена только к одному потоку. Каждый поток включает тогда некоторую последовательность работ. Сформиро­вав  потоков, можно перейти к составлению совокупностей работ. Совокупности работ, поступающих на обработку, образуются пу­тем выборки их из потоков П₁...П_. В начальный момент времени формируется первая совокупность, включающая  работ, взятых по одной из каждого потока. Эти работы поступают на соответст­вующие устройства при условии, что они не перегружают некото­рый общий ресурс. В качестве такого ресурса может выступать емкость оперативной памяти, поэтому для каждого момента форм­ирования совокупности работ должно соблюдаться ограничение: сумма емкостей памяти, занимаемых работами, включенными в со­вокупность, не должна превышать общей емкости памяти. Пусть в начальный момент совокупность работ имеет вид C₁={J₃, J₁,…,J₂}. Эта совокупность содержит  членов, из которых, как раньше приняли, работа J₁ принадлежит потоку П₂, а работа J₂ прянадлежит потоку П_. Ограничение по оперативной памяти примет вид V₃+ V₁ +... + V_i+... + V₂≤ V, где V — общий объем оперативной памяти; V_i — объем оперативной памяти, необходимый для работы i.

Если в некоторый момент времени завершается работа J₁, то на ее место в совокупность работ включается следующая работа из того же потока П₂. При этом опять проверяется ограничение.

Если оно не соблюдается, то выбирается следующая работа из данного потока. При отсутствии работ, соответствующих огра­ничению, может быть выбрана новая из другого потока.

Рассмотренные варианты планирования вычислительных работ при решении вычислительных задач являются классическими. Раз­работано большое число методов планирования, которые базиру­ются на теории расписаний. Принципы планирования работ широко используются в типовых операционных системах современных ЭВМ.