5. Информационный предел избыточности для канала с пакетными ошибками

В коммутируемых каналах появляются пакетные ошиб­ки. Под пакетной ошибкой кратности /понимают ошибку в коде, поражающую i символов. Пакеты ошибок обычно представляются последовательностью плохих состояний канала связи. Выделение хорошего и плохого состояния канала приводит к модели двоич­ного симметричного канала с памятью. В частном случае группирование ошибок в таком канале может быть описано с помощью простой цепи Маркова. Канал имеет произвольное число состоя­ний, однако должны быть заданы вероятности P_ij перехода канала из состояния i в состояние j. Наиболее простой вариант дискретного канала с памятью возникает при наличии двух состояний S₀ и S₁.

Вероятности переходов из одного состояния в другое задаются матрицей

,

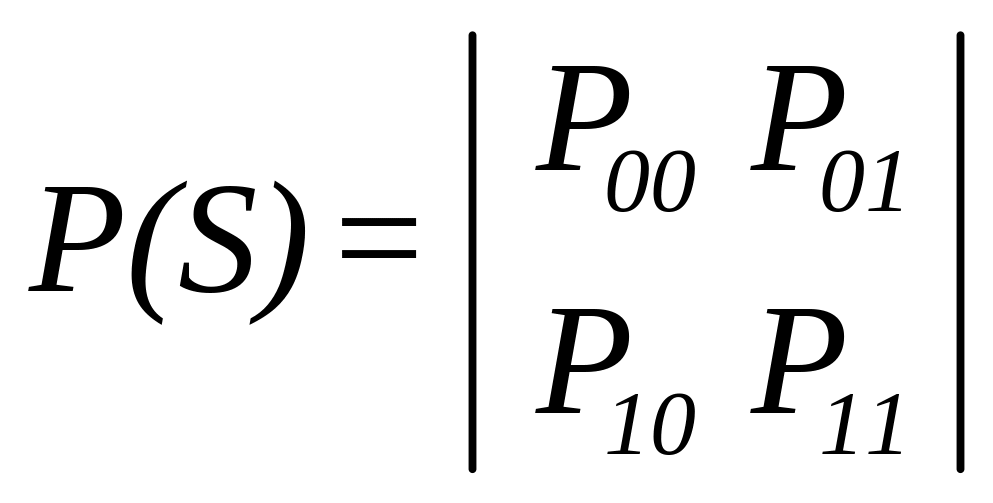где Р₀₀, Р₁₁ — вероятности сохранения состояний; P₀₀+P₀₁=P₁₀+P₁₁=1

Группирование ошибок возможно при соблюдении условий P₀₁«P₀₀; P₁₀«P₁₁. Данная модель была предложена Э. Гилбертом и предполагает наличие хорошего (безошибочного) состояния с ве­роятностью сохранения Р₀₀, когда ошибки отсутствуют, и плохого состояния с вероятностью сохранения Р₁₁, когда возникают независимые ошибки с вероятностью ис­кажения символа Р. Вероятности переходов могут быть отображены на графе модели дискретного сим­метричного канала с памятью, представленного на рис. 50.

Ве­роятность нахождения канала в хо­рошем состоянии составляет , соответственно вероя­тность нахождения канала в плохом состоянии — .

Сравним вероятность ошибки в двоичном симметричном канале без памяти с вероятностью ошибки в соответствующем канале с памятью. Ошибки возникают в состоянии канала S_l поэтому вероятность ошибки для канала с памятью . Нетрудно видеть, что Р_п«Р. Выделение плохого состояния канала связи позволяет моделировать пакеты ошибок как последователь­ность плохих состояний. Длина этих последовательностей обычно описывается геометрическим распределением. Пакеты ошибок на­кладываются на кодовую комбинацию, но не всегда вызывают искажение символа. Поэтому плохое состояние канала S₁ может быть подразделено на два состояния: правильное выявление элемен­тов кода и ошибка в выявлении. Плохое состояние канала с пра­вильным выявлением элементов обозначим S₁₀, плохое состояние с ошибочным выявлением — S₁₁ (рис. 51).

Тогда матрица переход­ных вероятностей принимает вид

.

Видно, что первый столбец матрицы соответствует состоянию канала S₀, второй столбец — состоянию S₁₀ и третий столбец — состоянию S₁₁. Модель независимых ошибок для плохого состояния канала связи позволяет аналитическим путем на основе аппарата производящих функций найти вероятность возникновения ошибок на длине кода n. Параметры дискретного симметричного канала с памятью могут быть найдены также на основе обработки резуль­татов экспериментальных исследований канала связи. Обычно вво­дят функцию распределения длин интервалов между ошибками и связывают параметры модели дискретного канала с памятью с результатами экспериментального исследования канала связи. Исследование коммутируемых телефонных каналов, используемых для передачи данных, показало, что P₁₀»P₀₁, вероятность ошибки может при этом меняться в достаточно широких пределах. Для канала с пакетными ошибками может быть установлен и инфор­мационный предел избыточности.

Если для передачи информации используется код, исправля­ющий s ошибок, при кодовом расстоянии d=2s+1, то количество контрольной информации составляет

,

где M(j,n) — число разновидностей ошибок с длиной пакета j в n элементном коде; Р(j) — вероятность возникновения пакетной ошибки с длиной j

.

Отсюда

.

Если допустить, что вероятности возникновения пакетной ошиб­ки любой кратности одинаковы, т. е. Р(0)=Р(1) = ... = Р(j) = ... = Р₁, то получаем

.

Из условия нормировки вероятностей P(j)=1. Отсюда

.

Количество контрольной информации

.

Информационный предел избыточности k_min=I_K для двоичного кода. Отсюда число контрольных элементов составляет

.

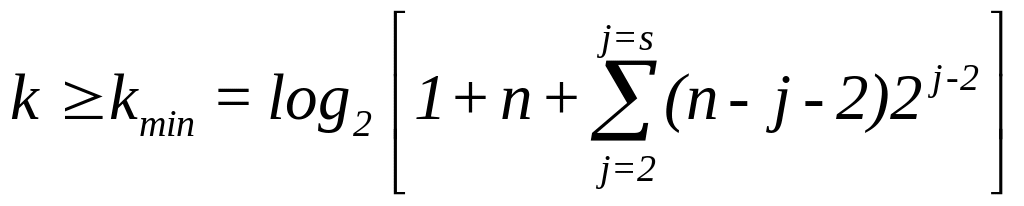В соответствии с этим информационным пределом могут быть построены корректирующие коды, которые оказываются целесооб­разными при равновероятных пакетных ошибках в дискретных ка­налах связи.

Модель Э. Гилберта является простейшей моделью дискретного симметричного канала с памятью. Некоторым обобщением этой модели может быть допущение ошибок не только в плохом, но и в хорошем состоянии. При этом матрица переходных вероят­ностей P(S) сохраняет свою справедливость, вводятся вероятности ошибки в хорошем Р(0) и плохом Р(1) состояниях. Связь с введен­ной ранее вероятностью ошибки Р определяется выражением

Р=Р(0)Р0+Р(1)Р1.

Развитием модели Э. Гилберта может быть введение ряда состо­яний каналов связи с соответствующими реальными значениями вероятностей ошибки. Большое значение на практике приобретают модели каналов связи, полученные на основе экспериментального исследования. Существует большое число таких моделей, которые пригодны для конкретных, достаточно ограниченных случаев при­менения.