4. Моделирование случайных воздействий на системы

При моделировании системы S методом имитационного моделирования, в частности методом статистического моделирования на ЭВМ, существенное внимание уделяется учету случайных факторов и воздействий на систему. Для их формализации используются случайные события, дискретные и непрерывные величины, векторы, процессы. Формирование на ЭВМ реализаций случайных объектов любой природы из перечисленных сводится к генерации и преобразованию последовательностей случайных чисел. Вопросы генерации базовых последовательностей псевдослучайных чисел {х_i}, имеющих равномерное распределение в интервале (0, 1), были рассмотрены во втором вопросе, поэтому остановимся на вопросах преобразования последовательностей случайных чисел {х_i} в последовательность {у_i} для имитации воздействий на моделируемую систему S.

Эти задачи очень важны в практике имитационного моделирования систем на ЭВМ, так как существенное количество операций, а значит, и временных ресурсов ЭВМ расходуется на действия со случайными числами. Таким образом, наличие эффективных методов, алгоритмов и программ формирования, необходимых для моделирования конкретных систем последовательностей случайных чисел {у_i}, во многом определяет возможности практического использования машинной имитации для исследования и проектирования систем.

Моделирование случайных событий. Простейшими случайными объектами при статистическом моделировании систем являются случайные события. Рассмотрим особенности их моделирования.

Пусть имеются случайные числа х_i, т.е. возможные значения случайной величины ξ, равномерно распределенной в интервале (0, 1). Необходимо реализовать случайное событие А, наступающее с заданной вероятностью р. Определим А как событие, состоящее в том, что выбранное значение x_i случайной величины ξ удовлетворяет неравенству

х_i ≤ р.

Тогда вероятность события А будет Р(А) = = p. Противоположное событие состоит в том, что х_i > р. Тогда Р( )= 1 - р.

Процедура моделирования в этом случае состоит в выборе значений х_i и сравнении их с р. При этом, если условие х_i ≤ р выполняется, исходом испытания является событие А.

Таким же образом можно рассмотреть группу событий. Пусть A₁, А₂, …, А_S – полная группа событий, наступающих с вероятностями p₁, р₂, …, р_S соответственно. Определим А_m как событие, состоящее в том, что выбранное значение х_i случайной величины ξ удовлетворяет неравенству

l_m-1 < x_i ≤ l_m,

где l_r = .

Тогда

Процедура моделирования испытаний в этом случае состоит в последовательном сравнении случайных чисел х_i со значениями l_r. Исходом испытания оказывается событие А_m, если выполняется условие l_m-1 < x_i ≤ l_m. Эту процедуру называют определением исхода испытания по жребию в соответствии с вероятностями p₁, p₂, …, p_S.

При моделировании систем часто необходимо осуществить такие испытания, при которых искомый результат является сложным событием, зависящим от двух (и более) простых событий. Пусть, например, независимые события А и В имеют вероятности наступления р_A и р_B. Возможными исходами совместных испытаний в этом случае будут события АВ, В, А , с вероятностями р_Aр_B, (1-p_A)p_B, p_A(1-p_B), (1-p_A)(1-p_B).

Для моделирования совместных испытаний можно использовать два варианта процедуры:

1) последовательную проверку условия х_i ≤ р;

2) определение одного из исходов АВ, В, А , по жребию с соответствующими вероятностями, т.е. аналогия l_m-1 < x_i ≤ l_m.

Первый вариант требует двух чисел х_i и сравнений для проверки условия х_i ≤ р. При втором варианте можно обойтись одним числом x_i, но сравнений может потребоваться больше. С точки зрения удобства построения моделирующего алгоритма и экономии количества операций и памяти ЭВМ более предпочтителен первый вариант.

Рассмотрим теперь случай, когда события А и В являются зависимыми и наступают с вероятностями р_A и р_B. Обозначим через Р (В/А) условную вероятность наступления события В при условии, что событие А произошло. При этом считаем, что условная вероятность Р(В/А) задана.

Рассмотрим один из вариантов построения модели. Из последовательности случайных чисел {х_i} извлекается очередное число х_m и проверяется справедливость неравенства х_m < р_A. Если это неравенство справедливо, то наступило событие А. Для испытания, связанного с событием В, используется вероятность Р (В/А). Из совокупности чисел {х_i} берется очередное число x_m+1 и проверяется условие х_m+1≤Р(В/А). В зависимости от того, выполняется или нет это неравенство, исходом испытания являются АВ или А .

Если неравенство х_m < р_A не выполняется, то наступило событие . Поэтому для испытания, связанного с событием В, необходимо определить вероятность

.

Выберем из совокупности {х_i} число x_m+1 и проверим справедливость неравенства

x_m+1 ≤ P(B/ ).

В зависимости от того, выполняется оно или нет, получим исходы испытания В или .

Рассмотрим особенности моделирования на ЭВМ марковских цепей, служащих, например, для формализации процессов в P-схемах. Простая однородная марковская цепь определяется матрицей переходов

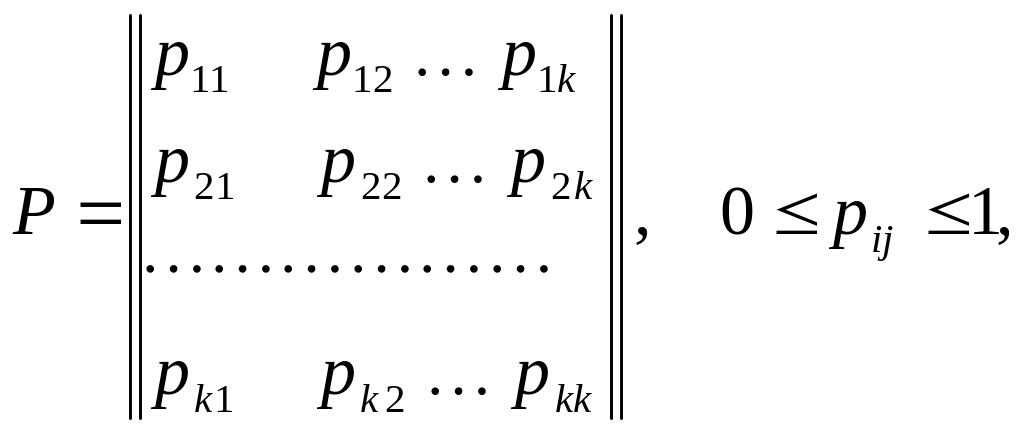
где p_ij – вероятность перехода из состояния z_i в состояние z_j.

Матрица переходов Р полностью описывает марковский процесс. Такая матрица является стохастической, т.е. сумма элементов каждой строки равна единице:

.

Обозначим через p_i(n), i= , вероятности того, что система будет находиться в состоянии z_i после n переходов. По определению,

Используя событийный подход, можно подойти к моделированию марковской цепи следующим образом. Пусть возможными исходами испытаний являются события A_l, А₂, .., A_k. Вероятность p_ij – это условная вероятность наступления события A_j в данном испытании при условии, что исходом предыдущего испытания было событие А_i. Моделирование такой цепи Маркова состоит в последовательном выборе событий А_j по жребию с вероятностями p_ij.

Сначала выбирается начальное состояние z₀, задаваемое начальными вероятностями р₁(0), p₂(0), …, p_k(0). Для этого из последовательности чисел {x_i} выбирается число х_m и сравнивается с l_r из (4.17), где в качестве р_i используются значения р₁(0), p₂(0), …, p_k(0). Таким образом выбирается номер m₀, для которого оказывается справедливым неравенство (4.17). Тогда начальным событием данной реализации цепи будет событие . Затем выбирается следующее случайное число х_m+1, которое сравнивается с l_r где в качестве p_i используются р_m0j. Определяется номер m₁, и следующим событием данной реализации цепи будет событие A_m1 и т.д. Очевидно, что каждый номер m_i определяет не только очередное событие А_mi формируемой реализации, но и распределение вероятностей р_mi1, р_mi2, …, р_mik для выбора очередного номера m_i+1, причем для эргодических марковских цепей влияние начальных вероятностей быстро уменьшается с ростом номера испытаний. Эргодическим называется всякий марковский процесс, для которого предельное распределение вероятностей p_i (n), i = , не зависит от начальных условий р_i(0). Поэтому при моделировании можно принимать, что

р₁(0) = p₂(0) = … = p_k(0) = 1/k.

Аналогично можно построить и более сложные алгоритмы, например для моделирования неоднородных марковских цепей.

Рассмотренные способы моделирования реализаций случайных объектов дают общее представление о наиболее типичных процедурах формирования реализаций в моделях процессов функционирования стохастических систем, но не исчерпывают всех приемов, используемых в практике статистического моделирования на ЭВМ.

Для формирования возможных значений случайных величин с заданным законом распределения исходным материалом служат базовые последовательности случайных чисел {х_i}, имеющие равномерное распределение в интервале (0, 1). Другими словами, случайные числа х_i как возможные значения случайной величины ξ, имеющей равномерное распределение в интервале (0, 1), могут быть преобразованы в возможные значения у_j случайной величины η, закон распределения которой задан.

Моделирование дискретных случайных величин. Рассмотрим особенности преобразования для случая получения дискретных случайных величин. Дискретная случайная величина η принимает значения у₁ ≤ у₂ ≤ ...≤ у_j ≤ ... с вероятностями p_l, р₂, ..., р_j, ..., составляющими дифференциальное распределение вероятностей

y у₁ y₂ …y_j …

Р(η = y) p₁ p₂ …p_j …

При этом интегральная функция распределения

.

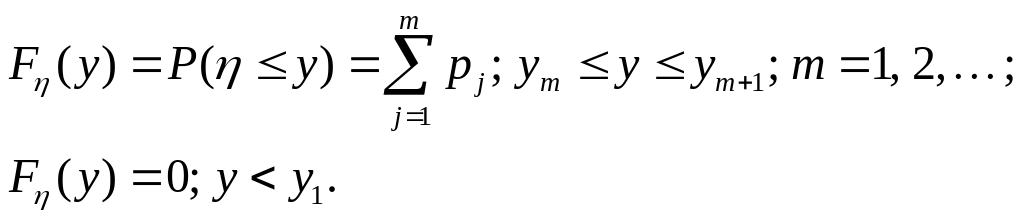Для получения дискретных случайных величин можно использовать метод обратной функции. Если ξ – равномерно распределенная на интервале (0, 1) случайная величина, то искомая случайная величина η получается с помощью преобразования

где – функция, обратная F_η.

Алгоритм вычисления по сводится к выполнению следующих действий:

если х₁ < р, то η = y₁, иначе

если х₂ < р₁ + р₂, то η = у₂, иначе,

………………………………………..

если х_j < , то η = y_m, иначе,

……………………………………..

При счете по данному алгоритму среднее число циклов сравнения .

Моделирование непрерывных случайных величин. Рассмотрим особенности генерации на ЭВМ непрерывных случайных величин. Непрерывная случайная величина η задана интегральной функцией распределения

где f_η(у) – плотность вероятностей.

Для получения непрерывных случайных величин с заданным законом распределения, как и для дискретных величин, можно воспользоваться методом обратной функции. Взаимно однозначная монотонная функция η = F^-1η (ξ), полученная решением относительно η уравнения F_η(y) = ξ, преобразует равномерно распределенную на интервале (0, 1) величину ξ в η с требуемой плотностью f_η(у).

Действительно, если случайная величина η имеет плотность распределения f_η(у), то распределение случайной величины

является равномерным в интервале (0, 1). На основании этого можно сделать следующий вывод. Чтобы получить число, принадлежащее последовательности случайных чисел {y_j}, имеющих функцию плотности f_η(у), необходимо разрешить относительно у_j уравнение

.

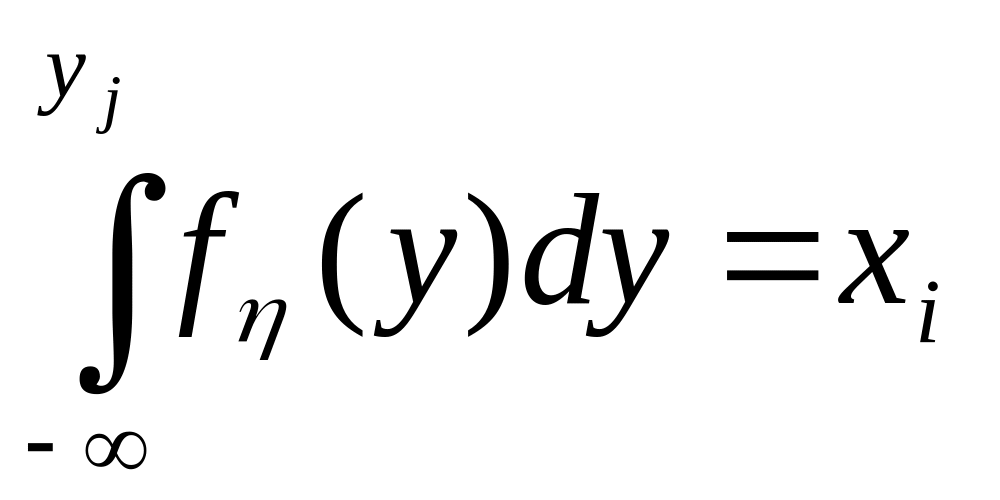Но этот способ получения случайных чисел с заданным законом распределения имеет ограниченную сферу применения в практике моделирования систем на ЭВМ, что объясняется следующими обстоятельствами:

1) для многих законов распределения, встречающихся в практических задачах моделирования, интеграл не берется, т.е. приходится прибегать к численным методам решения, что увеличивает затраты машинного времени на получение каждого случайного числа;

2) даже для случаев, когда интеграл берется в конечном виде, получаются формулы, содержащие действия логарифмирования, извлечения корня и т.д., которые выполняются с помощью стандартных подпрограмм ЭВМ, содержащих много исходных операций (сложения, умножения и т.п.), что также резко увеличивает затраты машинного времени на получение каждого случайного числа.

Поэтому в практике моделирования систем часто пользуются приближенными способами преобразования случайных чисел, которые можно классифицировать следующим образом:

а) универсальные способы, с помощью которых можно получать случайные числа с законом распределения любого вида;

б) неуниверсальные способы, пригодные для получения случайных чисел с конкретным законом распределения.

Рассмотрим приближенный универсальный способ получения случайных чисел, основанный на кусочной аппроксимации функции плотности. Пусть требуется получить последовательность случайных чисел {y_j} с функцией плотности f_η(у), возможные значения которой лежат в интервале (а, b). Представим f_η(у) в виде кусочно-постоянной функции, т.е. разобьем интервал (а, b) на m интервалов, как это показано на рис. 4.14, и будем считать f_η(у) на каждом интервале постоянной. Тогда случайную величину η можно представить в виде η=a_k+η_k*, где a_k – абсцисса левой границы k-гo интервала; η_k* – случайная величина, возможные значения которой располагаются равномерно внутри k-гo интервала, т.е. на каждом участке a_k-a_k+1 величина η_k* считается распределенной равномерно. Чтобы аппроксимировать f_η(у) наиболее удобным для практических целей способом, целесообразно разбить (а, b) на интервалы так, чтобы вероятность попадания случайной величины η в любой интервал (a_k, a_k+1) была постоянной, т.е. не зависела от номера интервала k. Таким образом, для вычисления a_k воспользуемся следующим соотношением:

.

Алгоритм машинной реализации этого способа получения случайных чисел сводится к последовательному выполнению следующих действий:

1) генерируется случайное равномерно распределенное число x_i из интервала (0, 1);

2) с помощью этого числа случайным образом выбирается интервал (a_k, а_k+1);

3) генерируется число х_i+1 и масштабируется с целью приведения его к интервалу (а_k, а_k+1), т.е. домножается на коэффициент (а_k+1 - а_k)х_i+1;

4) вычисляется случайное число y_j = аk + (a_k+1 - а_k)x_i+1 с требуемым законом распределения.

Достоинства этого приближенного способа преобразования случайных чисел: при реализации на ЭВМ требуется небольшое количество операций для получения каждого случайного числа, так как операция масштабирования вычисления интеграла выполняется только один раз перед моделированием, и количество операций не зависит от точности аппроксимации, т.е. от количества интервалов m.

2. ТИПОВЫЕ ИНФОРМАЦИОННЫЕ ПРОЦЕССЫ И ИХ МОДЕЛИ

1. Эталонная модель открытых систем

1. Базовые стандартные модели

1. Модель ISO OSI

Модель OSI (Open Systems Interconnection) является классическим приме­ром коммуникационной архитектуры. Она определяет семиуровневую модель взаимодействия вычислительных систем. Модель OSI — старейшая из моделей открытых систем.

Модель изложена в стандарте ISO 7498, состоящем из четырёх частей.

Архитектура OSI довольно абстрактна и охватывает очень широкий круг аспектов: общие принципы взаимодействия открытых систем, описание каждого из семи уровней, оборудование. Модель оперирует элементами архитектуры: системы, уровни, логические объекты, сервисы, протоколы, блоки данных, соединения - и определяет общие взаимоотношения между этими элементами.

Каждый уровень модели OSI (рис. 29) представляет собой группу взаимо­связанных функций обработки данных и связи между системами, которые могут быть выполнены стандартным образом с целью поддержки различных приложе­ний.

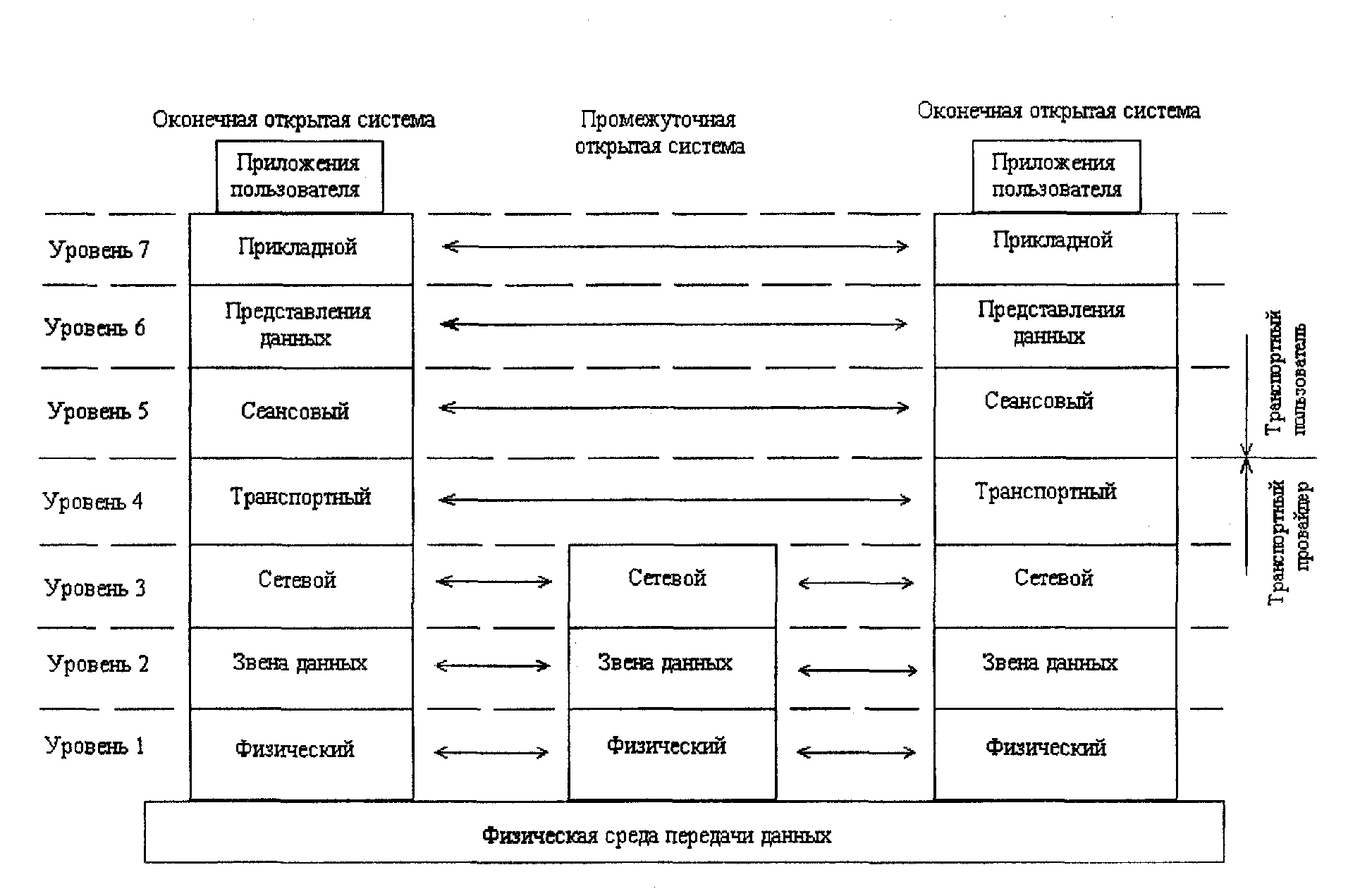
Рис. 29. Модель взаимосвязи открытых систем OSI

Каждый уровень обеспечивает хорошо определённый набор сервисов для вышележащего уровня и, в свою очередь, использует сервисы уровня, находяще­гося ниже его. Таким образом, процесс осуществления связи между системами разбивается на отдельные, легко управляемые блоки. Все вместе семь уровней обеспечивают коммуникационный сервис между оконечными пользователями (end-to-end). Изменения в протоколе любого уровня могут быть выполнены, не затрагивая соседних уровней.

Стандартизация взаимосвязи открытых систем проявляется в том, что на каждом уровне разрабатываются и утверждаются базовые стандарты двух видов:

определение сервиса уровня, которое в абстрактной форме описывает доступные извне услуги данного уровня;

спецификация протокола уровня, которая регламентирует взаимодейст­вие между равноправными объектами уровня, направленное на выполнение тре­буемого сервиса.

Верхние уровни модели связаны с логическими аспектами коммуникаций и ориентированы скорее на пользователей сети (обычно это — прикладные про­граммы), чем на саму инфраструктуру сети. Эти уровни включают механизмы для координации диалога между приложениями и для подготовки данных с целью обеспечения единой интерпретации их сторонами. Приложения могут иметь дос­туп к функциям этих уровней через соответствующие сервисы. Основные функ­ции верхних уровней — следующие:

Прикладной уровень (уровень 7) обеспечивает приложения необходимым высокоуровневым интерфейсом к нижележащим коммуникационным сервисам с целью обеспечения их связи с приложениями-партнёрами на других системах. К прикладному уровню также принято относить набор специализированных сервисов-приложений, таких как передача файлов, управление сообщениями, вирту­альный терминал, директориальный сервис и др. Этими сервисами могут, в свою очередь, пользоваться приложения конечного пользователя. Сами приложения пользователя считаются расположенными над прикладным уровнем.

Уровень представления данных (уровень 6) предназначен для согласова­ния синтаксиса и семантики данных для использования в процессе передачи дан­ных между системами.

Сеансовый уровень (уровень 5) обеспечивает сервисы координации диа­лога между системами: синхронизацию, полномочия, активности.

Нижние уровни обеспечивают транспортные функции сети: они ответст­венны за физические аспекты коммуникаций и доставку данных между оконеч­ными транспортными пользователями. Основные функции нижних уровней за­ключаются в следующем:

Транспортный уровень (уровень 4) обеспечивает надёжную и эффектив­ную доставку данных между любыми двумя абонентами потенциально ненадёж­ной сети передачи данных, независимо от характеристик и топологии сети.

Сетевой уровень (уровень 3) обеспечивает адресацию и маршрутизацию сообщений между системами, которые непосредственно не связаны друг с другом в сети. Модули данных на этом уровне обычно носят название "пакеты" или "дейтаграммы".

Уровень звена данных (уровень 2) связан с обменом неструктурирован­ными данными между смежными узлами сети. На этом уровне происходит обмен модулями данных — фреймами — и обеспечивается обнаружение и исправление ошибок передачи.

Физический уровень (уровень 1) предоставляет физическое соединение для передачи данных: среду распространения сигнала, интерфейсы, процедуры передачи сигналов по линии связи.

Уровни модели OSI можно сгруппировать в две категории, соответствую­щие понятиям "транспортный провайдер" (уровни 1 — 4) и "транспортный поль­зователь" (уровни 5 — 7).

Появление модели OSI послужило толчком к быстрому росту числа изде­лии и продуктов информационных технологий, согласующихся с концепцией от­крытых систем. Она стала основой разработки очень большого числа стандартов (как де-юре, так и де-факто), относящихся ко всем семи уровням этой модели. Однако они да­ют несколько «однобокий» взгляд на информационную систему: с точки зрения её коммуникационной инфраструктуры. В них не видны роль и функции опера­ционной системы. Кроме того, прикладной уровень профилей стал очень быстро «разрастаться», а простая семиуровневая модель оказалась неспособна описать всё многообразие компонентов этого уровня и соответствующих им стандартов.