2. Признак сравнения в предельной форме

Теорема 2. Пусть даны два ряда

(А) и

(В) .

Известно, что существует .

Если , то ряды (А) и (В) сходятся или расходятся одновременно.

Доказательство.

Возьмем такое, что . По определению предела для этого такой, что при всех выполняется неравенство

,

снимем модуль, получим .

Далее имеем

.

Теперь обратимся к признаку сравнения в форме неравенства. Если ряд (А) сходится, то по левой части неравенства сходится ряд (В). Если ряд (А) расходится, то по правой части неравенства расходится и ряд (В) и т.д. ■

Ряды, для которых выполняется условие этого признака, называются эквивалентными, будем использовать для них обозначение

~ .

Замечание. Случаи и рассмотреть самостоятельно.

Примеры.

Чтобы воспользоваться признаком сравнения в предельной форме, следует найти для исследуемого ряда эквивалентный ряд из числа эталонных рядов. Для этого вспомним понятие эквивалентных бесконечно малых и понятие главной части функции при предельном переходе. Общий член исследуемого ряда должен стремится к 0 (иначе ряд заведомо расходится), значит, следует найти для него эквивалентную бесконечно малую.

1) . Известно, что ~ , поэтому ~ . Ряд расходится, значит, расходится и ряд .

2) . Найдем предел общего члена

Проведенные действия показывают, что ~ .

Ряд сходится ряд сходится.

3). ~ , т.к. .

3. Признак Даламбера.

Этот признак сравнивает рассматриваемый ряд с геометрической прогрессией.

Теорема 3. Пусть ряд такой, что существует . Тогда

а) если , то ряд сходится;

б) если , то ряд расходится;

в) если , то однозначного ответа нет ( ряд может как сходиться, так и расходиться).

Доказательство.

а) Рассмотрим случай . Возьмем такое такое, что . По определению предела для этого такой, что при всех выполняется неравенство

, далее получаем, что . Начиная с номера запишем неравенства

,

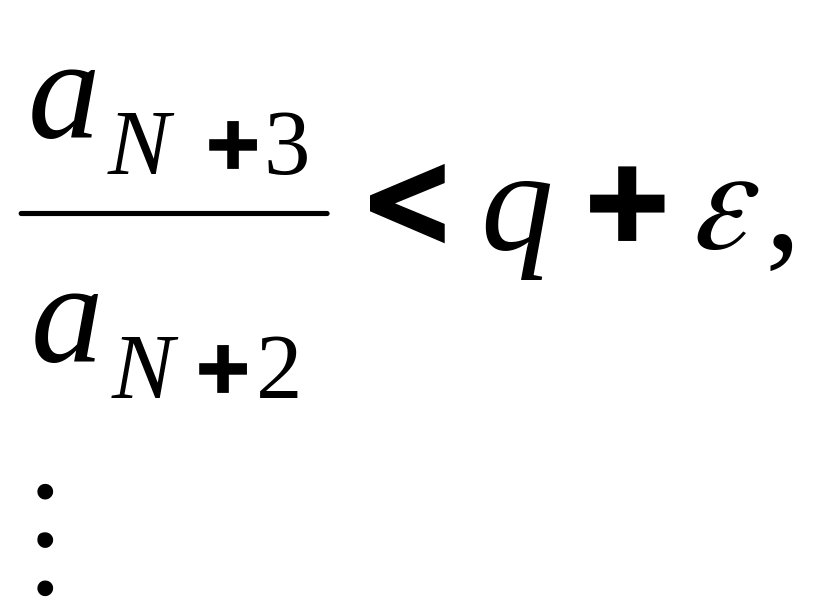
, где . Перемножим эти неравенства и получим

или

. Это неравенство показывает, что ряд имеет сходящуюся мажоранту ─ сумму бесконечно убывающей геометрической прогрессии со знаменателем . Значит, ряд сходится, а он является остатком данного ряда ряд сходится.

б) Пусть теперь . Возьмем такое такое, что . По определению предела для этого такой, что при всех выполняется неравенство

, далее получаем, что или . Полученное неравенство говорит о том, члены ряда возрастают общий член не стремится к 0 не выполнен необходимый признак сходимости ряд расходится.

в) Пусть, наконец, . Для каждого из рядов , верно, что , но первый ряд расходится, а второй сходится. ■

Пример.

. Найдем ряд сходится.

4. Признак Коши.

Теорема 4. Пусть для ряда существует . Тогда,

а) если , то ряд сходится;

б) если , то ряд расходится;

в) если , то однозначного ответа нет (ряд может как сходиться, так и расходиться).

Доказать самостоятельно.