Раздел V. Ряды

Г л а в а 1. Числовые ряды

§1. Определение числового ряда. Примеры

1⁰. Некоторые известные сведения о пределах.

Последовательность имеет предел , если для  такой номер , что для всех номеров выполняется неравенство . При этом пишут .

Примеры.

1. 

2. 

Если последовательность монотонна и ограничена, то она имеет предел.

2⁰.

Определение 1.

Пусть дана последовательность чисел . Выражение в виде бесконечной суммы (или ) называется числовым рядом. При этом называется индексом суммирования , а общим членом ряда.

Пусть дан ряд . Найдем конечные суммы:

Эти суммы называются частичными суммами ряда . Частичные суммы образуют последовательность

Определение 2.

Ряд называется сходящимся ( говорят, ряд сходится), если существует конечный предел последовательности частичных сумм, т.е. , при этом величина называется суммой ряда и записывается . В противном случае ряд называется расходящимся.

Примеры.

1. Запись рациональной дроби 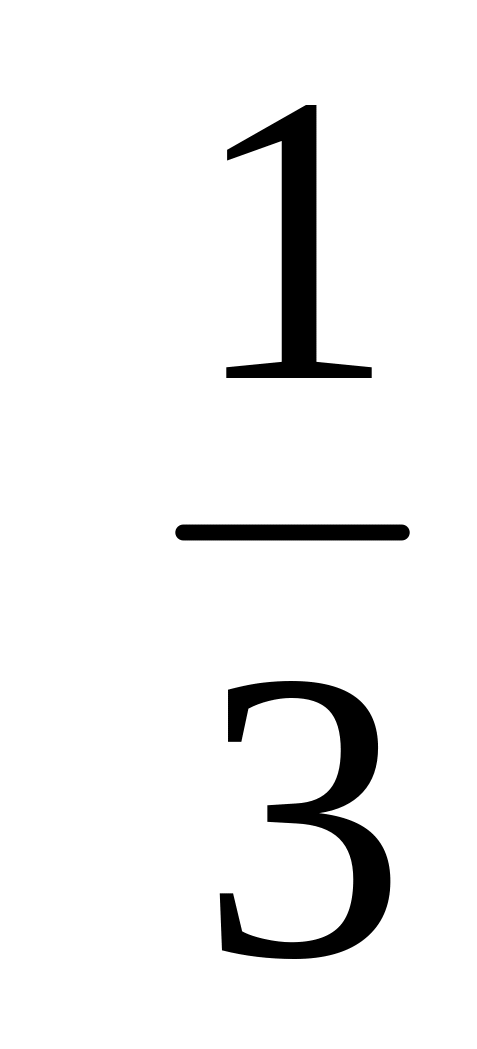в виде ,tпериодической десятичной дроби представляет собой сходящийся ряд, а именно .

2. Рассмотрим ряд

, его называют суммой геометрической прогрессии (напомним , что ─ знаменатель прогрессии).

Найдем формулу для его частичной суммы. Имеем . Умножим обе части равенства на и справа прибавим и вычтем . Тогда получим , откуда . Ясно, что при ряд расходится. В других случаях имеем

Таким образом, сумма бесконечно убывающей геометрической прогрессии равна .

Ряд сходится при и расходится при .

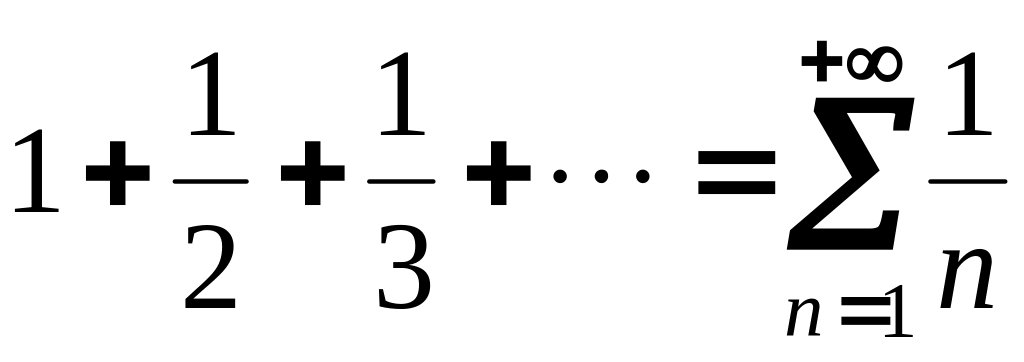3. Ряд называется гармоническим. ( Среднее гармоническое С двух чисел А и В находится из равенства , у данного ряда каждый член ряда, начиная со второго является средним гармоническим соседних).

Покажем, что предел частичных сумм этого ряда не существует.

Нарисуем гиперболу для . Обозначим площади криволинейных трапеций, образованных гиперболой, отрезками и вертикальными прямыми .

Ясно, что

.

Просуммируем эти неравенства. Слева найдем , справа получим частичную сумму

гармонического ряда. Неравенство говорит о том, что не существует конечного предела при . Таким образом, гармонический ряд расходится.

§2. Простейшие свойства сходящихся рядов

1. Если ряд сходится и имеет сумму , то ряд также сходится и имеет сумму . (Умножение ряда на неравное 0 число не влияет на его сходимость)

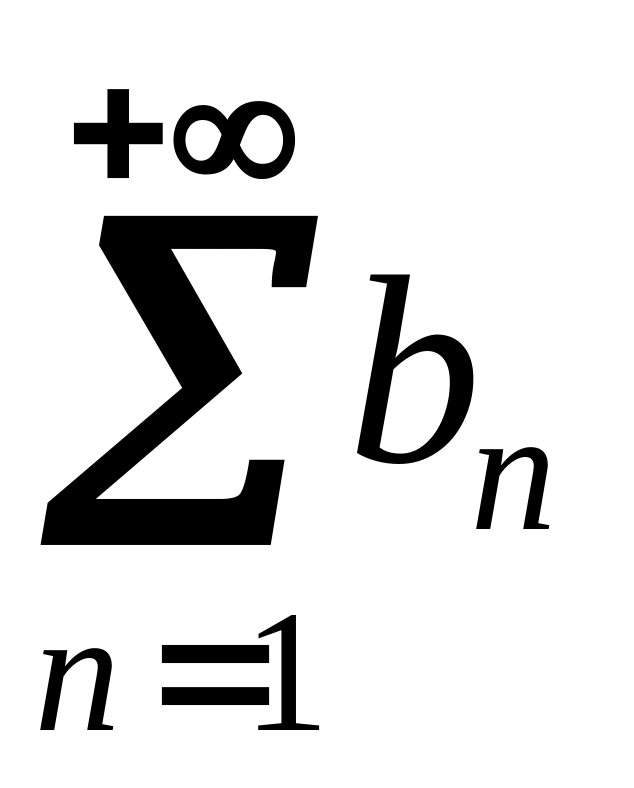2. Если ряды и сходятся, то сходится и ряд , полученный почленным сложением этих рядов.

Свойства I─II сразу следуют из определения сходимости ряда и свойств пределов.

3. Начнем с определения остатка ряда. Если в ряде отбросить некоторое количество первых слагаемых, то полученный ряд называется остатком исходного ряда.

Теорема. Если ряд сходится, то сходится и любой его остаток. И наоборот, из сходимости остатка ряда следует его сходимость.

Доказательство.

Пусть ряд сходится и имеет сумму , докажем, что сходится ряд при любом . Обозначим его частичные суммы . Для частичных сумм исходного ряда верно, что . При существует , значит, существует и .■

Обратное утверждение доказывается аналогично, доказать самостоятельно.

Замечание.

Доказанную теорему часто формулируют так: отбрасывание конечного числа первых членов ряда не влияет на его сходимость.

Обозначим сумму остатка (сходящегося ряда!), тогда можно записать . Так как , то .

4. Необходимый признак сходимости ряда.

Если ряд сходится, то его общий член стремится к 0, т.е. .

Доказательство сразу следует из равенства при : , .

Обратим внимание, что пример гармонического ряда показывает, что обратное неверно!

С другой стороны ясно, что если , то ряд заведомо расходится.