4. Статистическое описание результатов наблюдений для св y
Найдем
значения
и
из 100 чисел, длину разрядов
и границы интервалов
.
Результаты занесем в таблицу 3.
Таблица 3
Объем выборки |
n = |
100 |
Количество разрядов |
k = |
10 |
Длина разрядов |
h = |
2,4 |
Минимум |
ymin = |
32 |
Максимум |
ymax = |
56 |
Составляем интервальный ряд распределения для СВ Y.
Найдем
числа
значений СВ, попавших в каждый разряд
и частоту
попаданий значений СВ в каждый разряд
Плотность
частоты попаданий значений СВ в каждый
разряд рассчитаем по формуле
.
Полученные данные занесем в таблицу 4.
Для
определения статистической
плотности вероятности
вычисляем значения
.
Зависимость между h
и
оформим в виде графика: над каждым
интервалом
строим прямоугольник, высота которого
равна
(см.
рисунок 4).
Так как есть разряды, содержащие менее 5 значений, произведем объединение первых трех и последних двух разрядов. Соответствующие значения нанесем на рисунок 4 пунктирными линиями.
На рисунке 5 приведен полигон частот CB Y.
Для
построения статистической функции
распределения F*(y)
(см. рисунок 6) все значения СВ, попавшие
в j-ый
разряд, заменяем одним, совпадающим с
серединой разряда
и считаем, что это значение повторяется
раз.
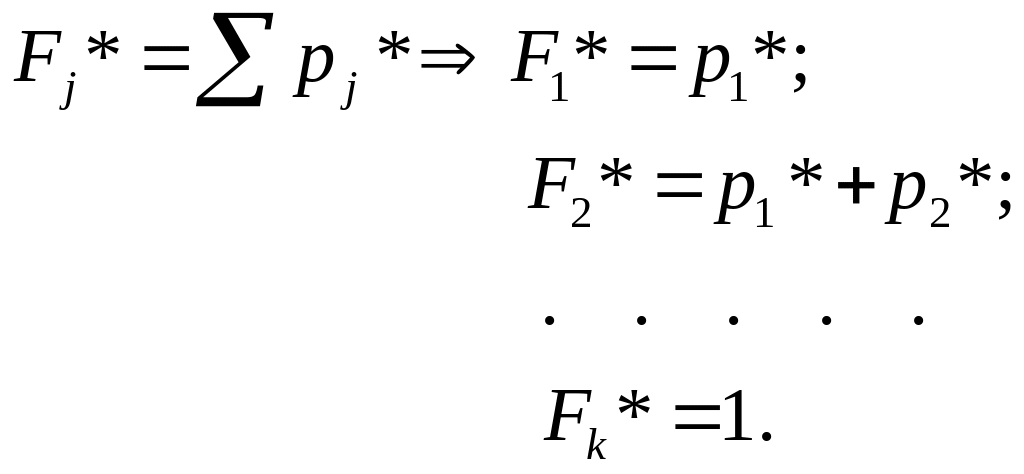
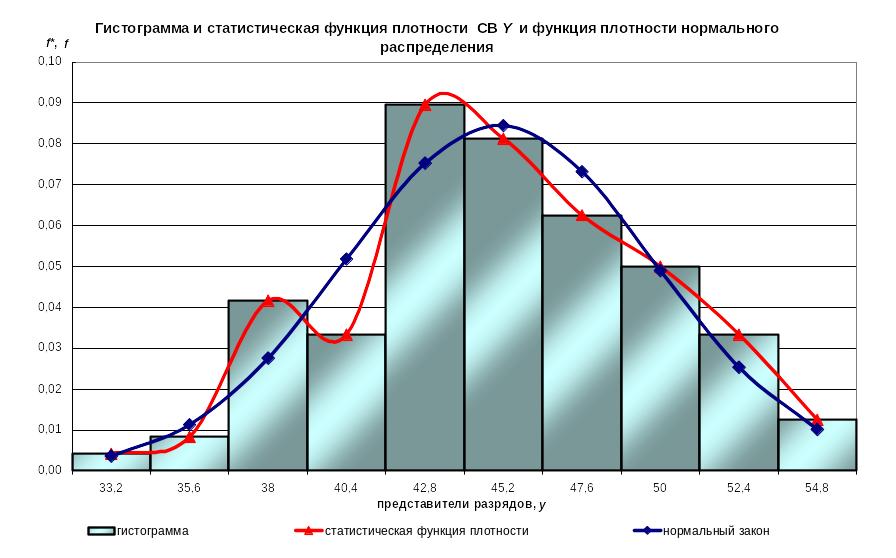
Р и с у н о к 4
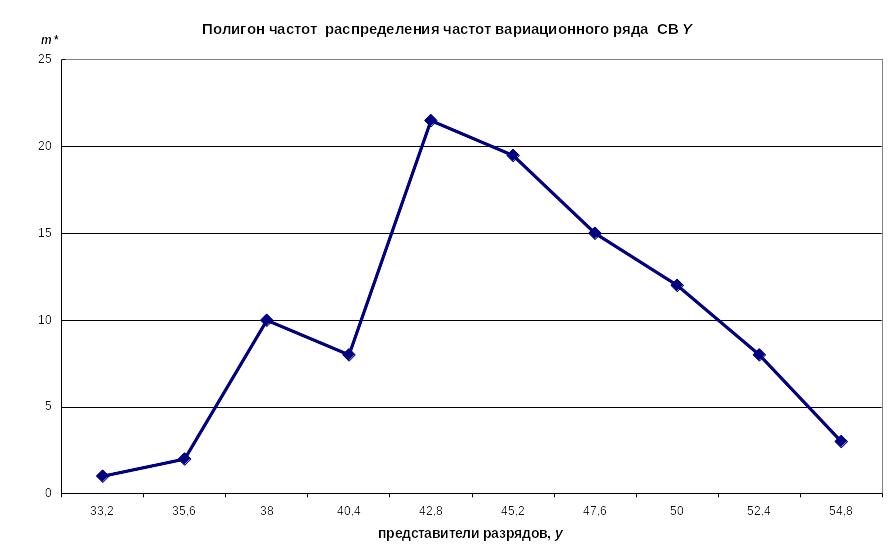
Р и с у н о к 5
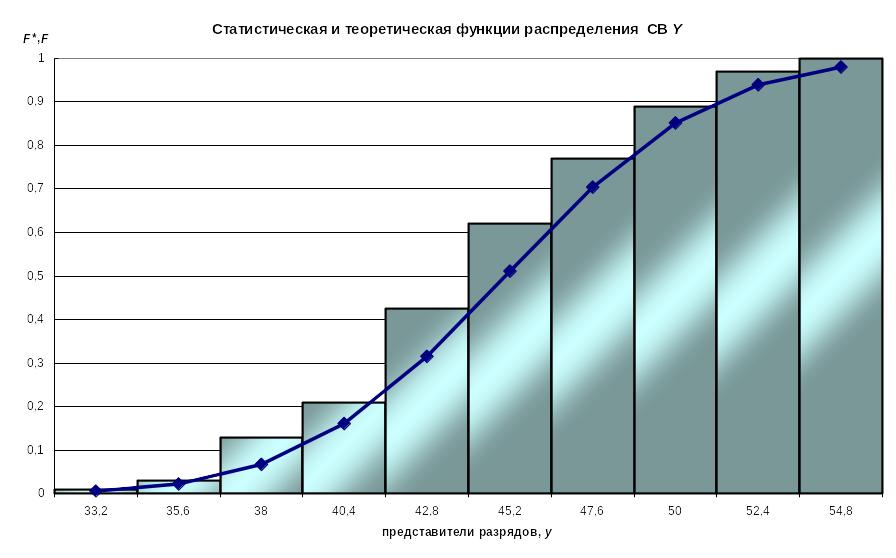
Р и с у н о к 6
Построим статистическую функцию распределения по значениям предпоследней строки таблицы 4 (см. рисунок 6).
5. Числовые характеристики, рассчитанные по интервальному ряду для св х
Находим статистические числовые характеристики по следующим формулам.
Оценку статистического среднего находим по формуле (для сгруппированных по разрядам данным)
,
где
значения
рассчитываются по формуле
.
Оценку статистической дисперсии рассчитываем по формуле
(для сгруппированных данных).
Исправленную
дисперсию рассчитываем по формуле
.
Статистическое среднее квадратическое отклонение и исправленное среднее квадратическое отклонение по определению равны
,
.
Эти
величины характеризует рассеивание
значений СВ относительно
и имеют размерность СВ Х.
Рассеивание
СВ также характеризуется статистическим
коэффициентом вариации
,
обычно выраженным в процентах:
.
Величина является безразмерной характеристикой величины разброса по отношению к величине статистического математического ожидания.
Медиану определяем по формуле
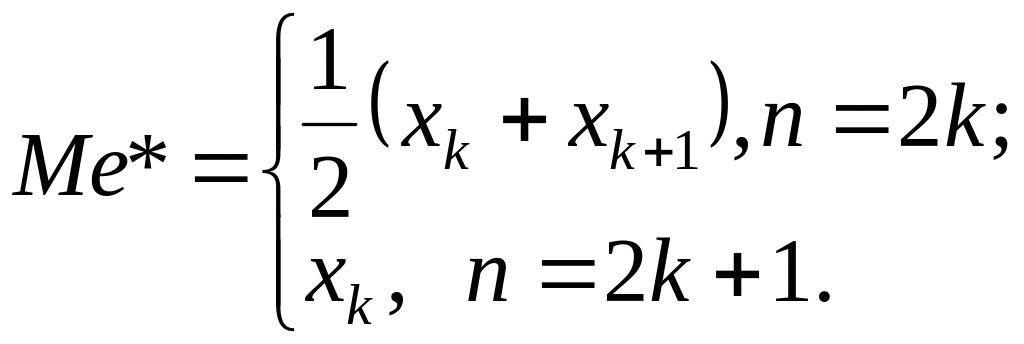
Мода
*
– варианта, соответствующая наибольшей
частоте. Итак, Ме*
= 80;
Мо*
= 83.
Все полученные данные заносим в таблицу 5.
Таблица 5
Математическое ожидание |
|
79,78 |
Дисперсия |
Dх* = |
125,42 |
Исправленная дисперсия |
|
126,67 |
Среднее квадратическое отклонение |
х* = |
11,2 |
Исправленное среднее квадратическое отклонение |
sx = |
11,26 |
Kоэффициент вариации |
v*х = |
14 % |
Мода |
Мо* = |
83 |
Медиана |
Ме* = |
80 |
=
=
Так как коэффициент вариации v*х = 14 % < 33 %, то выборка однородная.