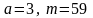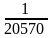- •Теорія чисел. Індивідуальне завдання № 2
- •1. Обчислити числові функції для значення n:
- •5. Перевірити, чи утворює дана множина зсл за модулем m? Висновки аргументувати. У разі негативної відповіді записати зсл за модулем m.
- •6. Знайти: а) останню цифру числа; б) дві останні цифри чисел;
- •7. Користуючись ознаками подільності:
- •8. Дослідити і розв’язати конгруенції першого степеня з однією невідомою.
- •9. Розв’язати невизначені лінійні (діофантові) рівняння в цілих числах.
- •10. А) Визначити довжину періоду і кількість цифр в передперіоді у розкладі в десятковий дріб дробу;
10. А) Визначити довжину періоду і кількість цифр в передперіоді у розкладі в десятковий дріб дробу;
б) знайти 2015 цифру після коми у розкладі в десятковий дріб дробу;
в)
указати порядок числа а
за даним модулем m
та розв’язати показникову конгруенцію
 ;
;
г) чи є а первісним коренем за даним модулем m? Скільки є первісних коренів за даним модулем?
Вар. |
Завдання 10 а |
Завдання 10 б |
Завдання 10 в, г |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
|
21 |
|
|
|
22 |
|
|
|
23 |
|
|
|
24 |
|
|
|
25 |
|
|
|