Лекція 7 Транспортна задача

(Т–задача). Постановка задачі. У пунктах постачання зосереджено однорідний вантаж відповідно в кількостях . Цей вантаж потрібно розвести в пунктів споживання відповідно в кількостях . Відома матриця витрат на перевезення одиниці вантажу від кожного пункту постачання до кожного пункту споживання (іноді задано відстані між цими пунктами):

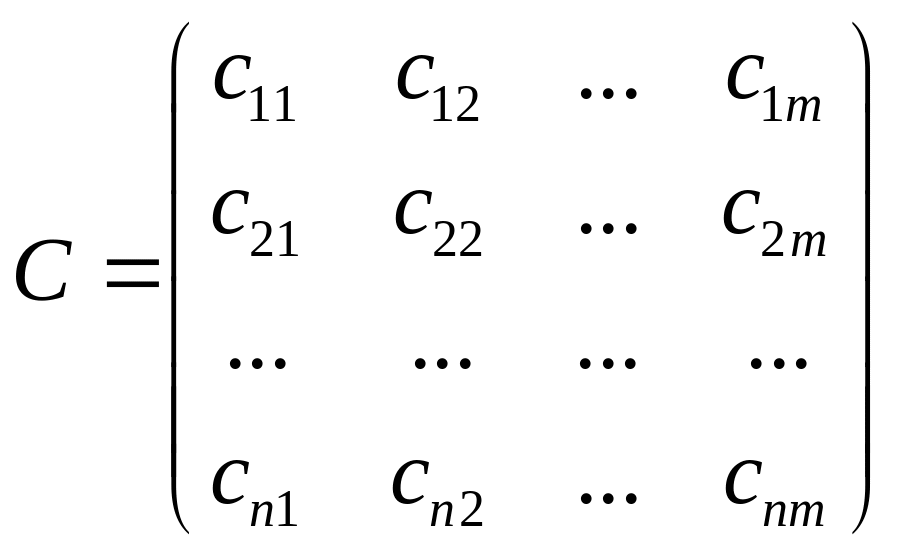. (9)

Скласти план перевезень вантажу з мінімальними затратами на перевезення.

Схема розв’язання. Запишемо математичну модель задачі. Нехай − кількість вантажу, який перевозять з –го пункту постачання в –й пункт споживання. Загальні затрати на перевезення, які необхідно мінімізувати, дорівнюють

. (10)

Системи обмежень, зумовлені відповідними запасами та потребами, мають вигляд

, . (11)

Якщо в ( ) загальні запаси і потреби збігаються , то така задача називається закритою, в іншому випадку – відкритою.

При розв’язуванні відкритої задачі спочатку її закривають, вводячи умовного споживача чи умовного постачальника, з ресурсом, що дорівнює різниці між загальними запасами та потребами. При цьому затрати на перевезення – нульові. Наприклад, якщо загальні запаси більші від потреб, то нульові затрати на перевезення означають, що частина вантажу ( ) залишається в пунктах постачання.

Існують як ручні, так і машинні методи розв’язання транспортних задач. Найпоширеніший серед ручних – метод потенціалів, який ми й розглянемо. До машинних належать: угорський метод, метод диференційних рент та інші.

Метод потенціалів. Розв’язування транспортної задачі починається з того, що ми спочатку складаємо перший план перевезень методом північно-західного кутка або методом мінімального елемента, який може бути досить далекий від оптимального. (Першу табличку в методі північно-західного кутка заповнюємо з верхнього лівого кутка, рухаючись вправо та вниз, вичерпуючи запаси й задовольняючи потреби, не враховуючи вартості перевезень. При складанні першого плану методом мінімального елемента відразу враховуємо вартість. У першу чергу заповнюють клітинки з мінімальними вартостями, звертаючи увагу на запаси та потреби).

Перевірка плану на оптимальність відбувається так званим методом потенціалів. Потенціали та знаходять із системи , яка складена за заповненими клітинками таблиці. Вартості перевезень записують у верхній правий куток клітинок. Заповнених клітинок у першій, та й в інших таблицях має бути .

Якщо для всіх незаповнених (вільних) клітинок виконується нерівність (після того як знайдені потенціали заповнених клітинок) , то план оптимальний. У протилежному випадку його можна поліпшити, зробивши цикл перерахунку (сукупність знаків “+” та “−” , які ставляться лише на „поворотах” на заповнених клітинках, крім першого “+”, з якого починається перерахунок). Перший “+” (початок циклу) ставиться в незаповненій клітинці, в якій не виконується нерівність з найбільшою розбіжністю. Серед клітинок з “мінусами” вибираємо найменше перевезення і складаємо нову таблицю, в якій там, де знак “ плюс” цей мінімум додаємо, а де “мінус” – віднімаємо. Нова таблиця (новий план) поліпшена. Продовжуючи цей процес, ми врешті-решт прийдемо до таблиці, в якій для всіх вільних клітинок буде виконуватись вказана нерівність. І тоді останній план буде оптимальний.

При переході від однієї таблиці до іншої можна спостерігати, як зменшуються загальні витрати на перевезення, обчислюючи значення цільової функції для кожної таблиці (плану).

Приклад 4. Розв’язати Т–задачу

Розв’язання. Заповнимо першу таблицю методом північно-західного кутка.

Таблиця 1

	100		150		150		80		120
300	100	1	150	3	−	4	+	2		5	0
					50
100		2		4	+	1	−	3		2	−3
					100		0
200		3		1		5		6		1	0
							80		120
	1		3		4		6		1

Заповнених клітинок тут має бути , тому довелось заповнити одну клітинку “хибним” нулем. Причому його варто вписати там, де менша вартість перевезень і щоб заповнені клітинки утворювали східчасту фігуру.

Обчислюємо потенціали заповнених клітинок із системи . Ця система із 7 рівнянь має 8 невідомих. Для зручності беремо і легко знаходимо всі інші потенціали, заповнюючи їх у таблицю 1.

Тепер перевіряємо виконання нерівностей для вільних клітинок:

6 + 0 2; 1+ 0 5; 1 – 3 2; 3 – 3 4; 1 – 3 2; 1 + 0 3; 3 + 0 1;

4 + 0 5.

Перша і передостання нерівності не вірні. У першій розбіжність на 4 одиниці, у передостанній – на 2. Вибираємо “гіршу”, ставимо в ній “+”, і складаємо цикл перерахунку. Знаходимо мінімум серед перевезень де проставлений знак “−”: .

Заповнюємо нову таблицю 2, в якій: де знак “плюс”, цей мінімум додаємо, де знак “мінус” – віднімаємо.

Таблиця 2

	100		150		150		80		120
300	100	1	− 150	3		4	+	2		5	0
					50		0
100		2		4		1		3		2	−3
					100
200		3	+	1		5	−	6		1	4
							80		120
	1		3		4		2		−3

.

Вартість перевезень не змінилась, тому що 0 просто перекочував в іншу клітинку. Знову перераховуємо потенціали заповнених клітинок і діємо аналогічно до попереднього.

Таблиця 3

	100		150		150		80		120
300	100	1	70	3		4		2		5	0
					50		80
100		2		4		1		3		2	−3
					100
200		3		1		5		6		1	−2
			80						120
	1		3		4		2		3

.

Для всіх вільних клітинок виконується нерівність, яка гарантує оптимальність плану.

Відповідь: ,

всі інші . .