Лекція 3 § 3. Наближені методи розв’язування систем лінійних алгебраїчних рівнянь

Точні методи розв’язування систем лінійних рівнянь характеризуються тим, що виконуючи скінченну кількість обчислень (кроків) ми отримуємо точний розв’язок, якщо коефіцієнти при невідомих і вільні члени задані точно і у процесі обчислень не велось заокруглень. На практиці часто заокруглюються проміжні значення при складанні систем рівнянь і тому фактично така система описує наближено стан об’єкта. Тому часто розв’язують системи рівнянь наближеними методами використовуючи при цьому комп’ютерні програми.

1. Метод простої ітерації лінійних систем. Розглянемо систему лінійних рівнянь із невідомими:

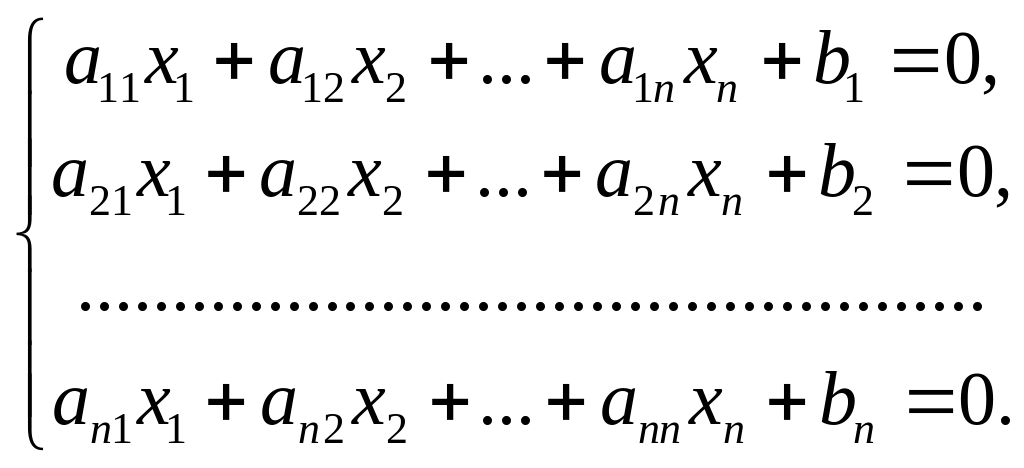(1)

Переставимо рівняння системи таким чином, щоб діагональні елементи і запишемо їх у вигляді . Систему (1) у вигляді

Звідси, поділивши кожне рівняння системи відповідно на та перепозначивши коефіцієнти

,

отримаємо:

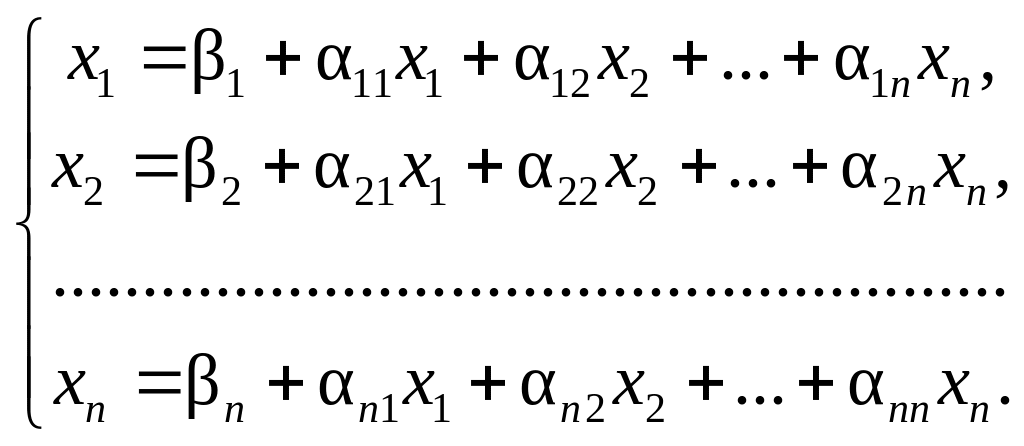(2)

У ряді випадків, наприклад, у ручному режимі розв’язання зручно брати , тоді невідомі не входять у праву частину го рівняння.

Приймемо у якості нульового наближення значення невідомих Підставляючи їх у праву частину системи (2), отримаємо перше наближення

(3)

Продовжуючи аналогічні підстановки, отримаємо е наближення

(4)

Описаний принцип вибору нульового наближення та схема знаходження наближень (4) називається простою ітерацією. Процес послідовних наближень є збіжним якщо існують скінченні границі . Умова збіжності: процес розв’язання системи (1) є збіжним якщо матриця коефіцієнтів при невідомих є матрицею з діагональною перевагою, тобто для всіх значень виконується умова

(5)

Проте, матриця коефіцієнтів при невідомих часто не задовольняє умови (5), однак цього можна інколи добитися перестановкою рівнянь системи.

Якість наближеного розв’язку можна оцінити порівнянням го наближення з м наближенням. Вважаючи е наближення точним значенням, визначають відносну похибку . Якщо всі не перевищують деякої заданої величини (потрібної точності) то процес завершено і за розв’язок беруть е наближення.

Приклад 1. Розв’язати методом простої ітерації систему рівнянь з відносною похибкою яка не перевищує 5%

Розв’язання. Переставимо рівняння так щоб виконувались умови (5)

Працюючи в ручному режимі, визначимо відповідно з першого, другого і третього рівняння попередньої системи, матимемо:

В якості нульового наближення візьмемо . Перше наближення згідно з формулою (3)

Знайдемо відносні похибки нульового наближення

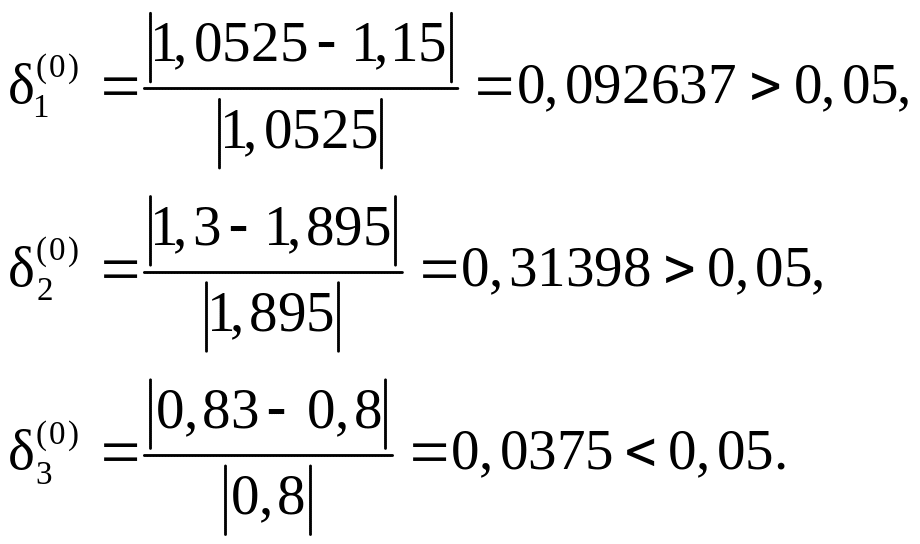
Оскільки потрібної точності ще не досягнуто, знаходимо друге наближення та похибки першого наближення

Знаходимо третє наближення та похибки

Отже, результати третього наближення можна прийняти в якості шуканого розв’язку. Зауважимо, що точним розв’язком системи є значення до яких можна наблизитись методом ітерації з довільною, наперед заданою, точністю.

Метод простої ітерації володіє унікальною властивістю яка полягає в тому, що якщо у процесі обчислень була допущена помилка, метод сам виправляє її, проте це збільшить кількість ітерацій.

2. Метод Зейделя розв’язування лінійних систем. У методі простої ітерації процес обчислень невідомих у кожному наближенні заснований на значеннях попереднього наближення. Метод Зейделя при обчисленні невідомого в м наближенні враховує уже обчислені в цьому наближенні величини . Умови збіжності методу Зейделя такі ж як у методі ітерації (перевага діагональних елементів матриці коефіцієнтів при невідомих). Метод Зейделя швидше приводить до результату. Продемонструємо це на попередньому прикладі. Нульове наближення таке ж .

Перше наближення

Друге наближення

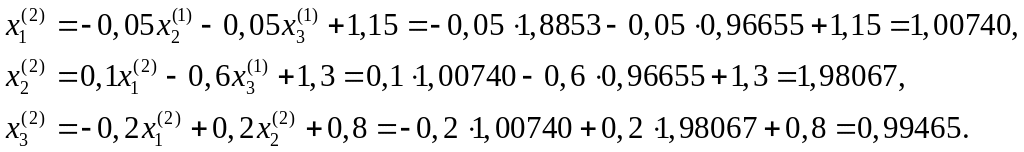
Результати другого наближення методом Зейделя практично співпадають із значеннями невідомих, отриманих методом простої ітерації у третьому наближенні.

Вправа. Методами простої ітерації та методом Зейделя розв’язати систему рівнянь, щоб відносна похибка кожного значення не перевищувала 5%. Обчислення проводити до п’яти значущих цифр

Відповідь:

3. Метод Гаусса. Розв’язування систем лінійних рівнянь за методом Гаусса описано у розділі 1 (§3). Якщо система лінійних рівнянь громіздка або коефіцієнти десяткові дроби з кількома значущими цифрами після коми, то в цьому випадку зручно реалізовувати розв’язування на ЕВМ. Для цього достатньо вказати алгоритм, згідно з яким матриця (коефіцієнтів біля невідомих) перетворюється до трикутного вигляду і вказати відповідні перетворення правих частин системи.

Не проводячи повних викладок, запишемо як перетворюються коефіцієнти системи лінійних рівнянь

(6)

у ході виключення невідомих із системи:

, (7)

. (8)

Обчислення правих частин трикутної системи здійснюється за формулами

, (9)

. (10)

Коефіцієнти і праві частини зберігаються у пам’яті комп’ютера і використовуються при здійсненні оберненого ходу

. (11)

Основним обмеженням методу є припущення про те, що не всі елементи на які проводиться ділення відмінні від нуля. Число називається ведучим елементом на му кроці виключення. Навіть тоді, коли ведучий елемент близький до нуля у процесі обчислень може накопичуватись значна похибка. Проте вихід із такої ситуації є. Він полягає в тому, що у якості ведучого елемента беруть не , а коефіцієнт який найбільший за модулем. Тобто виключають не наступну за номером невідому, а невідому коефіцієнт при якій найбільший.

Приклад 2. Розв’язати систему лінійних рівнянь методом Гаусса використавши стандартну програму

Program Gauss;

var a:array[1..20,1..21] of real;

b:array[1..20,1..21] of real;

x:array[1..20] of real;

prom:real;

n,n1,i,j,j1,k:integer;

begin

writeln(‘n-?’);

readln(n);

n1:=n+1;

for i:=1 to n do

for j:=1 to n1 do

begin

writeln(‘a[‘,i,’,’,j,’]-?’);

readln(a[i,j]);

b[i,j]:=a[i,j];

end;

for i:=1 to n do

begin

prom:=a[i,j];

for j:=i to n1 do

a[i,j]:=a[i,j]/prom;

for k:=i+1 to n do

prom:=a[k,i];

begin

for j:=1 to n1 do

a[k,j]:=a[k,j] - a[i,j]*prom;

end;

end;

x[n]:=a[n,n+1]/a[n,n];

for j:=n-1 downto 1 do

begin

x[j]:=a[j,n1];

for j1:=j+1 to n do

x[j]:=x[j]-a[j,j1]*x[j1];

end;

for i:=1 to n do

writeln(‘x[‘,i,’]=’,x[i]:5:3;

end.

Результат: X[1]=2,73916

X[2]=1,61536

X[3]=-2,58081

X[4]=-3,44523.