Вправи для аудиторної роботи Завдання 1. Побудувати інтерполяційні многочлени Ньютона та Лагранжа для функції , яка задана таблицею
1.
-
1
3
4
4
7
Обчислити значення
побудованої функції в точці
та визначити відносну похибку, якщо
відомо що
.
2.
-
0
4
6
4
7
Обчислити значення
побудованої функції в точці
та визначити відносну похибку, якщо
відомо що
.
3.
-
2
5
7
9
0
12
3
1
Обчислити значення
побудованої функції в точці
та визначити відносну похибку, якщо
відомо що
.
4.
-
1,5
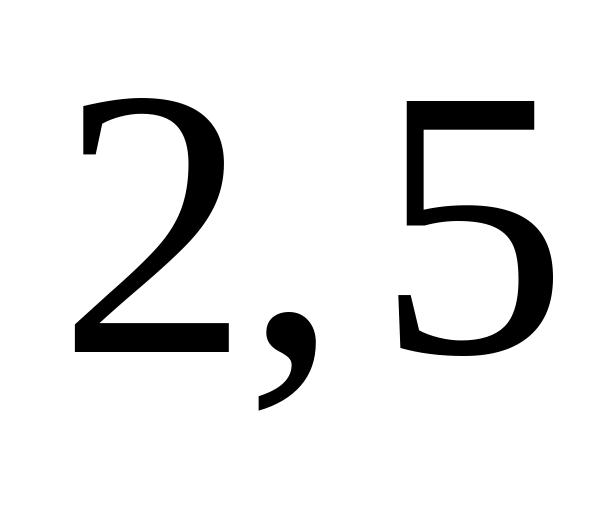
3,5
4,5
-2
0,5
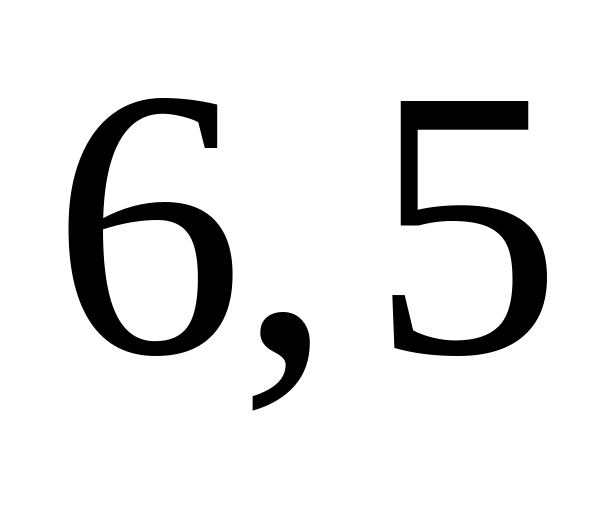
Обчислити значення
побудованої функції в точці
та визначити відносну похибку, якщо
відомо що
.
Завдання 2. Розв’язати графічно задачі ЛП:
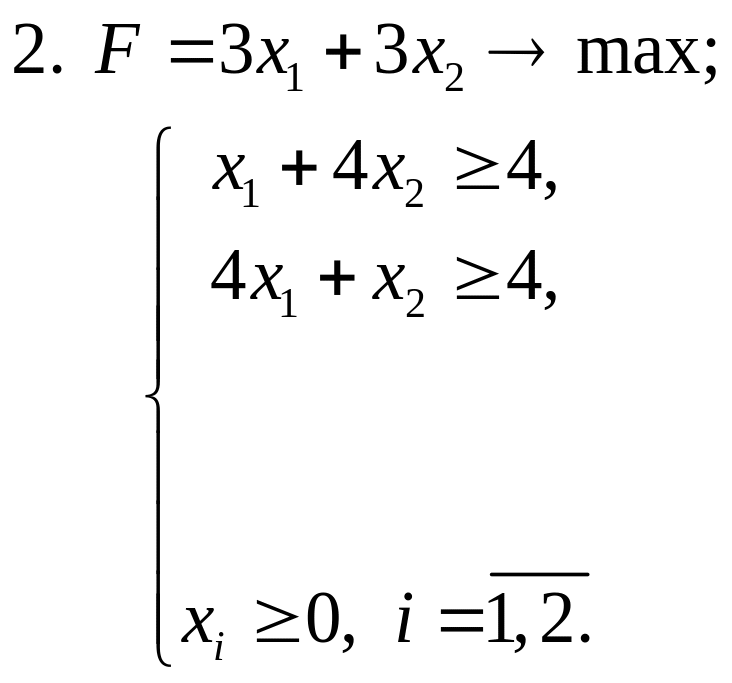
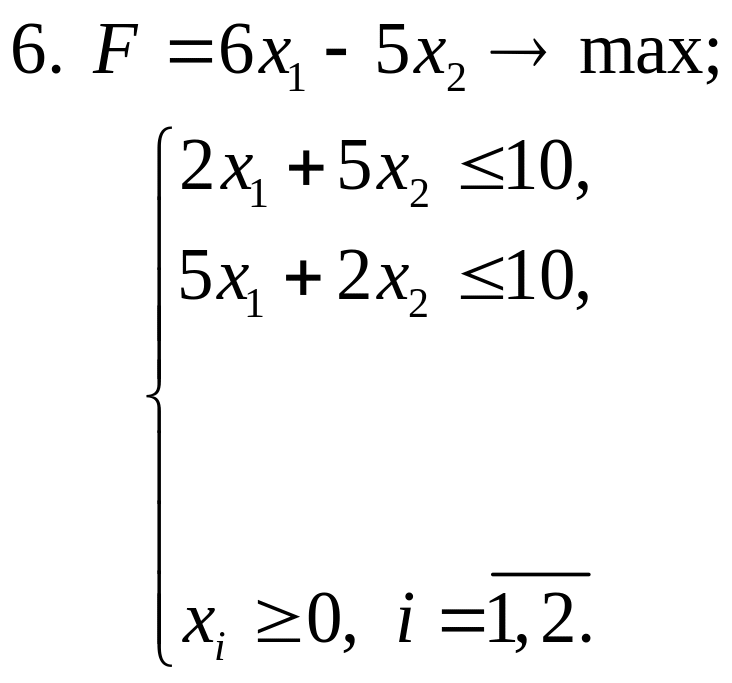
Завдання 3. Розв’язати задачі ЛП симплекс-методом:
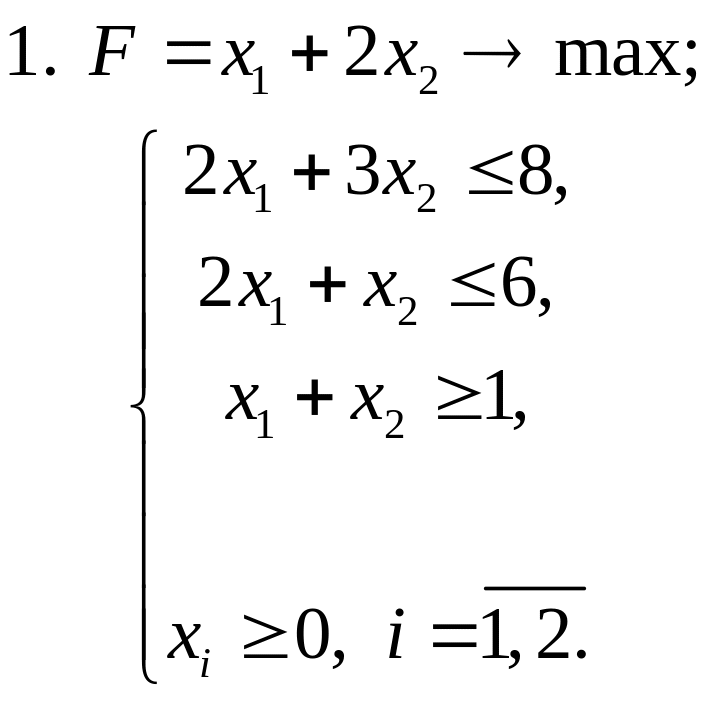
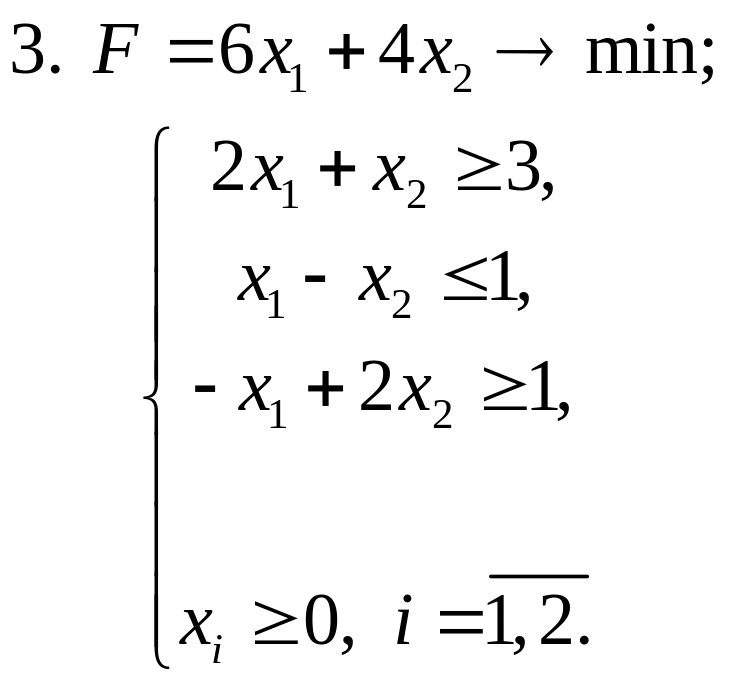
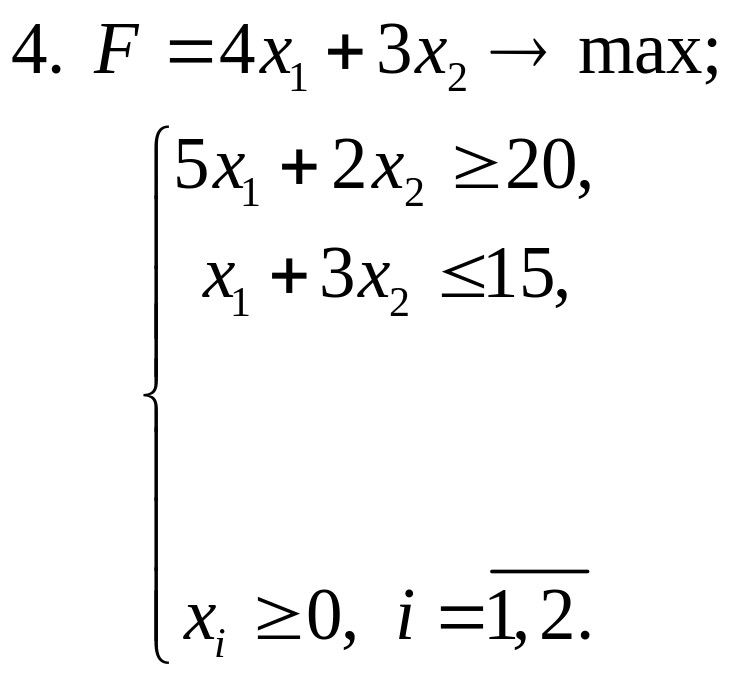
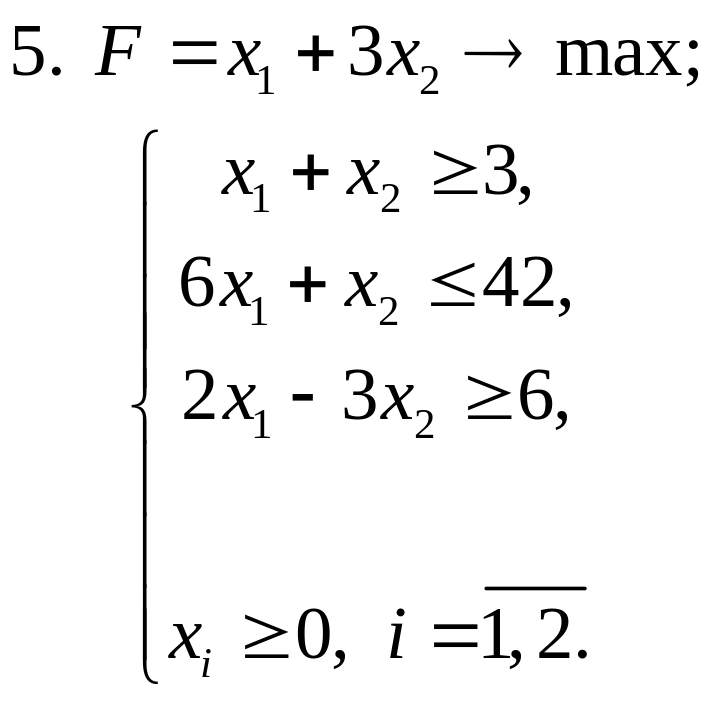
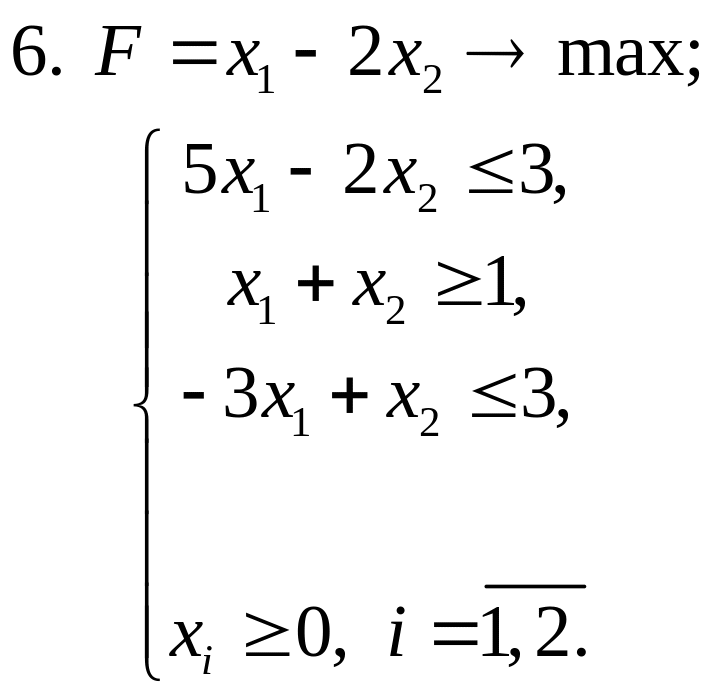
Завдання 4. Розв’язати транспортні задачі (знайти мінімальні затрати на перевезення):
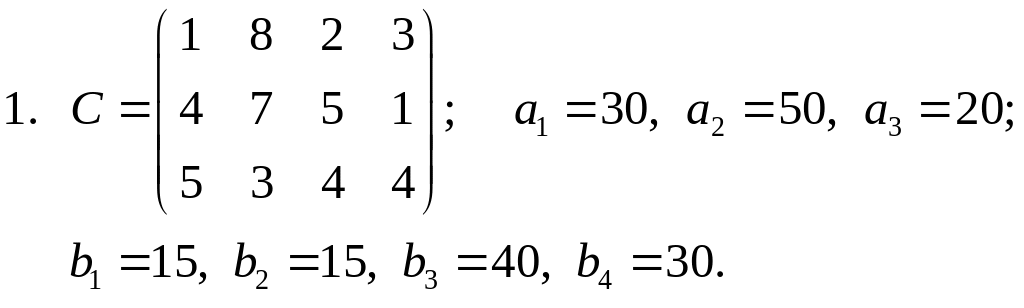
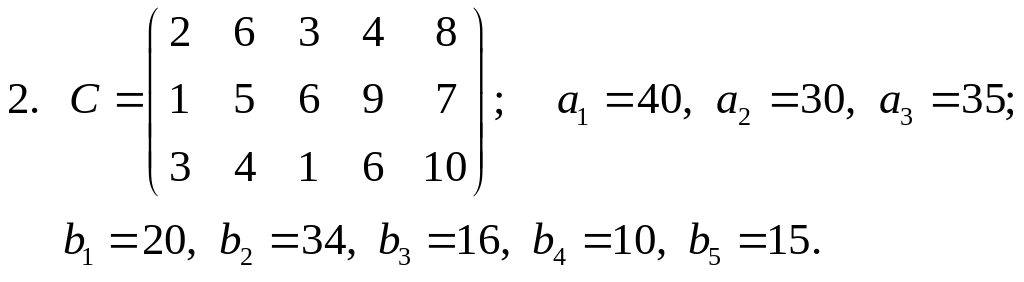
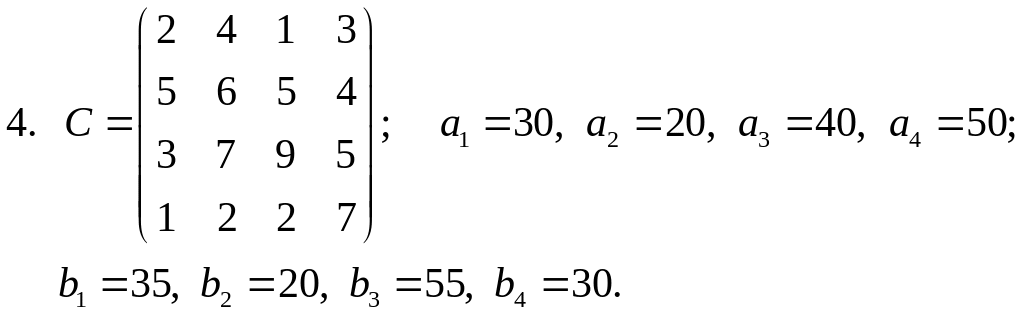
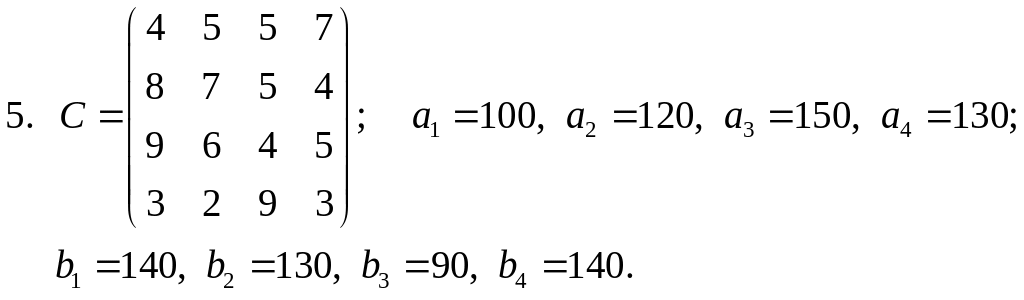
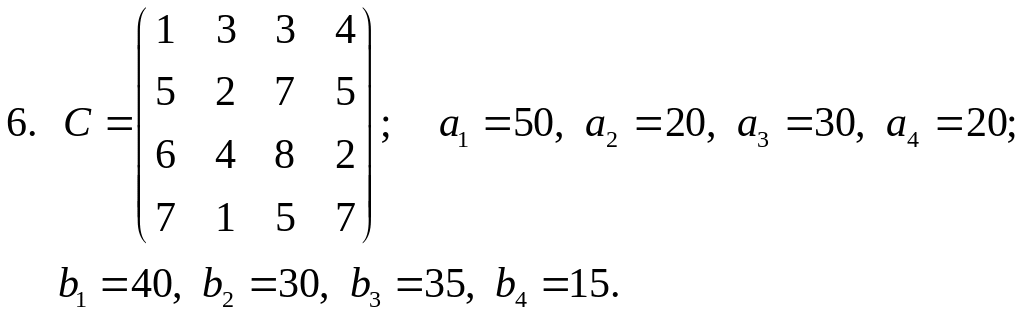
Завдання 5. Розв’язати задачі квадратичного програмування
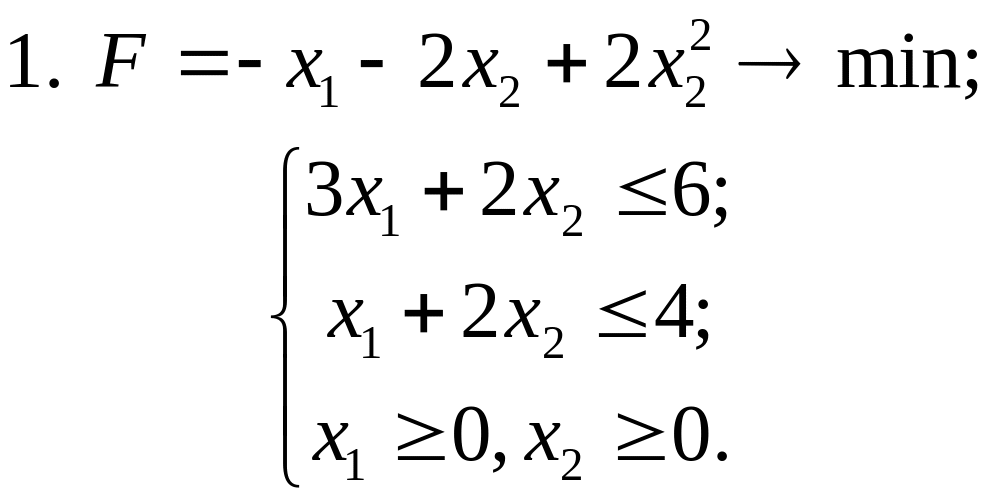
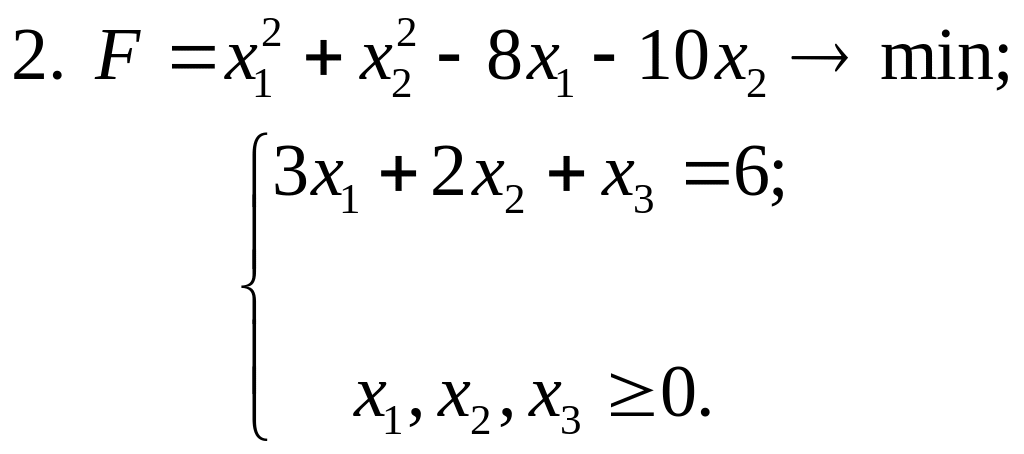
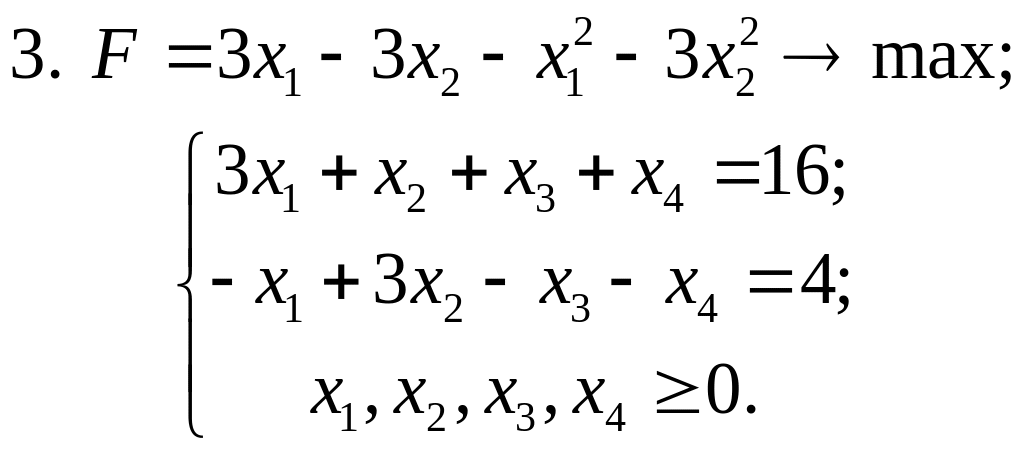
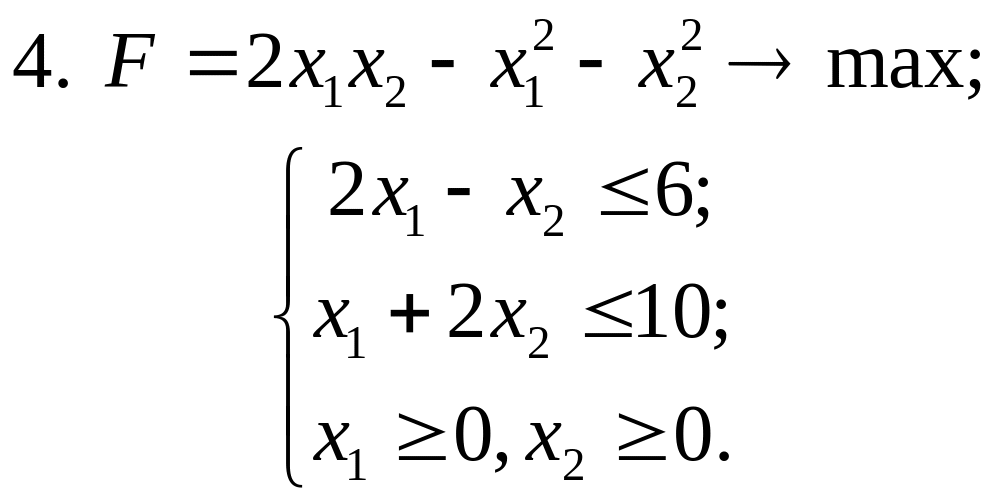
Завдання 6. Статистичні методи обробки експериментальних даних
Побудувати статистичний ряд, гістограму та емпіричну функцію розподілу за вибіркою:
1,2; 8,6; 3,5; 10,8; 9,3; 7,1; 4,1; 7,9; 2,2; 10,0; 3,2; 8,3; 4,7; 3,8; 5;
0,25; 4,0; 5,7; 7,2; 4,5; 3,5 6,4; 3,2; 8,6; 7,0; 5,9; 3,4; 6,2; 3,9; 4,1;
4,5; 3,2; 5,4; 6,5; 4,6; 2,5; 5,8; 7,5; 6,4; 9,5; 6,8; 8,2; 4,8; 3,7; 5,9.
Побудувати полігон частот та емпіричну функцію розподілу вибірки; знайти вибіркові середню та дисперсію; визначити моду і медіану; середнє лінійне відхилення і коефіцієнт варіації
|
|
|
|
|
|
|
|
|
|
2)
|
|
|
|
|
|
|
|
|
|
3)
|
|
|
|
|
|
|
|
|
|
У
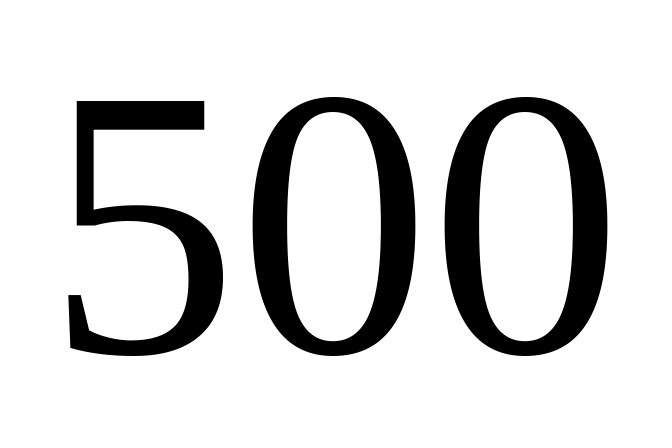однотипних радіоламп була перевірена
сила анодного струму, причому у
з них вона виявилась вища від тієї, що
гарантована паспортом. Знайти з
коефіцієнтом довір’я
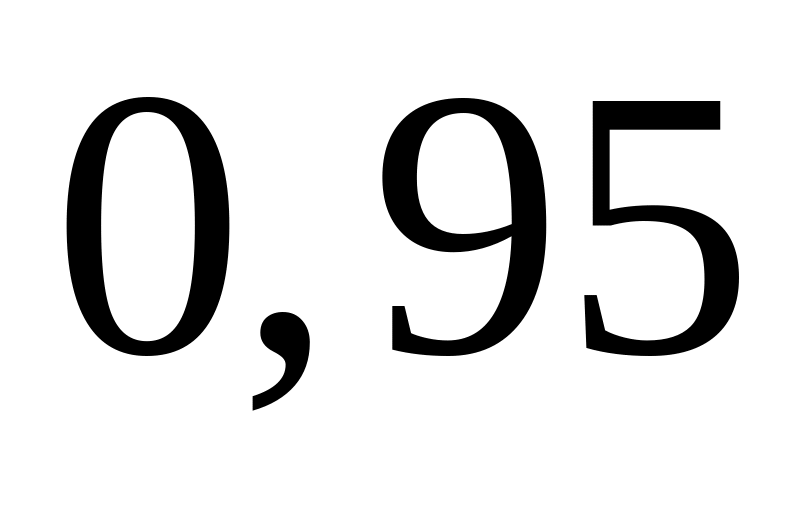інтервал, який містить частка таких
радіоламп серед усіх радіоламп даного
типу.
Відповідь:
.
Виміряна максимальна ємність 20 конденсаторів (у пікофарадах)
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
4,4 |
4,31 |
4,4 |
4,4 |
4,65 |
4,56 |
4,71 |
4,54 |
4,36 |
4,56 |
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
4,31 |
4,42 |
4,6 |
4,35 |
4,5 |
4,4 |
4,43 |
4,48 |
4,42 |
4,45. |
Знайти вибіркову
середню, вибіркову дисперсію і її
незміщену оцінку, оцінити точність
оцінки математичного сподівання з
надійністю
,
використовуючи асимптотичний нормальний
розподіл
.
Відповідь:
,
.
Дано ріст ціни будівельних матеріалів (у відсотках) на
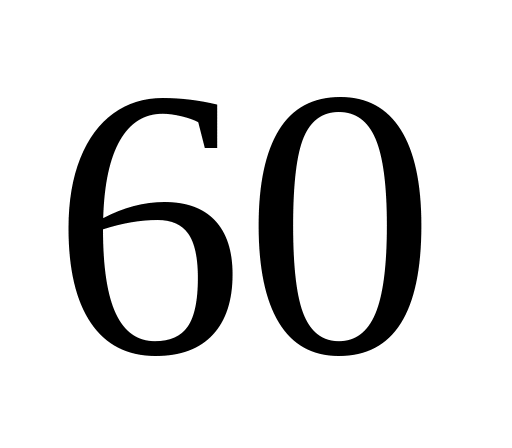підприємствах збуту порівняно з
попереднім місяцем. Побудувати полігон
розподілу для неперервного варіаційного
ряду, взявши за значення ознаки середини
інтервалів. Перевірити гіпотезу про
нормальний розподіл генеральної
сукупності, яку представляє вибірка,
скориставшись критерієм χ2.
104,9 101,3 104,2 105,9 104,0 106,8 104,4 104,3 102,7 105,1
103,9 106,6 104,5 104,1 106,8 105,0 103,4 106,0 105,5 103,4
106,0 105,5 104,8 104,4 107,0 103,3 104,5 105,0 102,8 103,6
105,1 102,4 108,0 102,2 103,7 104,1 103,9 101,6 104,1 105,1
101,2 103,1 104,2 101,8 104,9 106,1 102,9 102,6 107,2 104,3
103,1 105,2 102,8 103,4 103,9 108,3 101,5 104,7 106,9 104,8
Зроблено групування промислових підприємств області за розміром росту валової продукції (у відсотках) порівняно з минулим роком
Валова продукція, % |
80 – 90 |
90 – 100 |
100 – – 110 |
110 – – 120 |
120 – – 130 |
130 – – 140 |
Кількість підприємств |
6 |
15 |
34 |
29 |
18 |
15 |
Вважаючи емпіричний розподіл близьким до нормального, побудувати гістограму частот, емпіричну і теоретичну криві та перевірити гіпотезу про нормальний розподіл генеральної сукупності за критерієм Пірсона.
Методом кореляційного аналізу дослідити залежність між ознаками. Розрахувати коефіцієнти регресії та кореляції. Побудувати графік кореляційної залежності.
1,0
4,1
3,6
3,9
1,2
4,2
3,5
4,5
3,2
2,6
15,5
12,5
9,6
8,5
3,5
2,8
5,7
6,8
4,3
4,7
-
5,0
2,8
4,1
3,5
2,5
5,3
3,0
4,5
4,7
5,4
8,0
15,5
7,6
13,5
10,5
9,5
12,5
9,3
14,3
16,8
|
4,1 |
5,0 |
2,5 |
4,2 |
4,9 |
3,5 |
6,0 |
3,8 |
5,3 |
6,9 |
|
27 |
19 |
22 |
20 |
15 |
25 |
18 |
29 |
16 |
14 |