5. Елементи кореляційного аналізу. Рівняння лінійної регресії

Для багатьох задач практики часто доводиться досліджувати залежність досліджуваної величини від іншої величини. Дві випадкові величини можуть бути зв’язані або функціональною залежністю, або статистичною, або бути незалежними.

Залежність називають статистичною, якщо зміна однієї величини веде до зміни розподілу іншої. Зокрема, якщо при зміні однієї з величин змінюється середнє значення іншої, то в цьому випадку статистична залежність називається кореляційною. Це записують так:

(20)

Рівняння (20) називають рівнянням лінії регресії на . Графік функції називають лінією регресії на .

У теорії кореляції важливою є задача встановлення форми зв’язку між корельованими величинами та їх тіснота.

Найчастіше зустрічається лінійний кореляційний зв’язок, тому рівняння лінії регресії для цього випадку має вигляд

. (21)

Тісноту кореляційного зв’язку оцінюють коефіцієнтом кореляції , який приймає значення з проміжку .

Коефіцієнт кореляції обчислюється за формулою

r_в= , (22)

де − середні арифметичні корельованих величин, а − їх середньоквадратичні відхилення.

Якщо абсолютна величина коефіцієнта кореляції близька до одиниці, то зв’язок між величинами та вважається тісним, чим ближче до нуля, тим зв’язок слабший.

Якщо вибірка має достатній обсяг і добре представляє (репрезентує) генеральну сукупність, то висновок про тісноту зв’язку між ознаками, зроблений на основі вибіркової сукупності, може бути поширений і на генеральну сукупність. Тут є потреба перевірити значимість вибіркового коефіцієнта кореляції. Для цього обчислюється спостережуване значення критерію

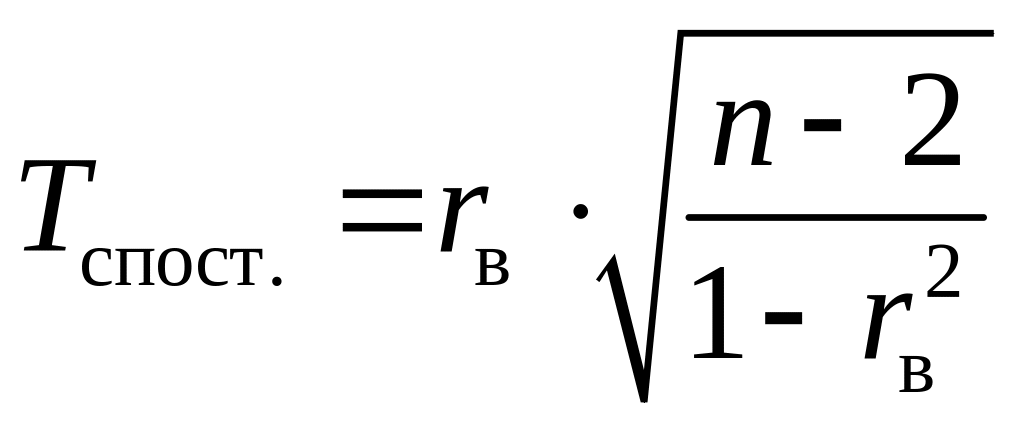. (23)

При заданому рівні значимості та числі степенів вільності за таблицею розподілу Стьюдента визначаємо критичне значення .

Якщо , то вибірковий коефіцієнт кореляції вважається незначним, тобто величини та вважаються некорельованими. У випадку нерівності , вибірковий коефіцієнт кореляції значно відрізняється від нуля, тоді вважається, що розглядувані величини корельовано і можна записати рівняння лінійної регресії

, (24)

де , .

Приклад. Дано дози внесення мінеральних добрив та їх вплив на врожайність зернових на один гектар площі в господарствах:

	1,0	2,0	3,0	4,0	1,0	4,0	2,0	1,0	3,0	3,0
	20	25	27	29	22	30	25	21	25	26

Методом кореляційного аналізу дослідити залежність між ознаками. Побудувати графік кореляційної залежності.

Розв’язання. Складемо розрахункову таблицю для проміжних і результуючих обчислень, врахувавши, що .

				( )
1,0	20	−1,4	1,96	−5	25	7,0
2,0	25	−0,4	0,16	0	0	0
3,0	27	0,6	0,36	2	4	1,2
4,0	29	1,6	2,56	4	16	6,4
1,0	22	−1,4	1,96	−3	9	4,2
4,0	30	1,6	2,56	5	25	8,0
2,0	25	−0,4	0,16	0	0	0
1,0	21	−1,4	1,96	−4	16	5,6
3,0	25	0,6	0,36	0	0	0
3,0	26	0,6	0,36	1	1	0,6
24	250	0	12,44	0	96	33,0

За даними таблиці знаходимо коефіцієнт кореляції

.

Спостережуване значення ознаки .

За рівнем значимості і числом ступенів вільності знаходимо з таблиці критичних точок Стьюдента .

Оскільки спостережуване значення критерію більше за критичне , то можна вважати, що величини і корельовані. Визначимо коефіцієнт регресії та запишемо рівняння лінії регресії (рис. 2).

, ,

.