
- •Лекція 1-2 § 1. Наближені обчислення
- •§ 2. Інтерполяція функцій
- •Лекція 3 § 3. Наближені методи розв’язування систем лінійних алгебраїчних рівнянь
- •Лекція 4 § 4. Лінійне та нелінійне програмування
- •Лекція 5
- •Лекція 6 Метод штучної бази
- •Лекція 7 Транспортна задача
- •Лекція 8 а (на вибір)
- •Лекція 8 б (на вибір)
- •Лекція 9 – 10 – 11 ( матеріал на вибір) § 6. Статистична обробка експериментальних даних
- •1. Варіаційні ряди
- •2. Оцінка невідомих параметрів за вибіркою
- •3. Побудова інтервалів надійності
- •4. Перевірка статистичних гіпотез
- •5. Елементи кореляційного аналізу. Рівняння лінійної регресії
- •Вправи для аудиторної роботи Завдання 1. Побудувати інтерполяційні многочлени Ньютона та Лагранжа для функції , яка задана таблицею
- •Індивідуальні розрахунково-графічні роботи Завдання 1. Побудова інтерполяційних многочленів Ньютона та Лагранжа
- •Завдання 2. Розв’язати графічно задачі лп
- •Завдання 3. Розв’язати задачі лп симплекс-методом
- •Завдання 4. Розв’язати транспортні задачі
- •Завдання 5. Розв’язати задачі нелінійного програмування
- •§2. Інтерполяція функцій ………………………………………………5
1. Варіаційні ряди
Нехай вимірюється
деяка фізична величина
![]() .
Розміри замірів у кожному випадку можна
розглядати як незалежні спостереження
випадкової величини
.
Розміри замірів у кожному випадку можна
розглядати як незалежні спостереження
випадкової величини
![]() :
:
![]() .
Якщо прилад, яким вимірюється ця фізична
величина, не дає систематичних похибок,
то
.
Якщо прилад, яким вимірюється ця фізична
величина, не дає систематичних похибок,
то
![]() .
Таким чином, за незалежними спостереженнями
можна оцінити невідомий параметр. У
цьому випадку можна висунути гіпотезу
про нормальний закон розподілу вибіркової
сукупності. Перевірку гіпотези можна
здійснювати за відомими критеріями
узгодження, які гарантують з певною
ймовірністю висновок про нормальний
розподіл генеральної сукупності.
.
Таким чином, за незалежними спостереженнями
можна оцінити невідомий параметр. У
цьому випадку можна висунути гіпотезу
про нормальний закон розподілу вибіркової
сукупності. Перевірку гіпотези можна
здійснювати за відомими критеріями
узгодження, які гарантують з певною
ймовірністю висновок про нормальний
розподіл генеральної сукупності.
Сукупність всіх можливих значень випадкової величини називають генеральною сукупністю. Генеральна сукупність може бути як скінченною, так і нескінченною.
Для того, щоб вибіркова сукупність несла найбільш важливі властивості генеральної сукупності, вибірка має бути репрезентативною (представницькою), тобто представляти реальний стан справ. У різних галузях виробництва напрацьовані свої методи встановлення репрезентативності вибірки.
Статистичний матеріал, отриманий у результаті спостережень, записують у вигляді простого варіаційного ряду, тобто таблиці, яка складається з двох рядків: у першому рядку записується номер спостереження , у другому – значення (варіанта) вимірюваної величини. Загальну кількість спостережень називають обсягом вибірки.
Коли значення
варіанти повторюються, і статистичний
матеріал великий за обсягом, варіаційний
ряд зручно розміщувати у вигляді
ранжированого
варіаційного ряду, тобто таблиці, в якій
в першому рядку записано значення ознаки
в порядку зростання (спадання)
,
а в другому – частота відповідної
варіанти
![]() або відносна частота відповідної
варіанти
або відносна частота відповідної
варіанти
![]() .
.
Статистичний розподіл вибірки можна також записувати у вигляді послідовності інтервалів і відповідних їм частот. За частоту інтервалу приймають суму частот варіант, які попадають у цей інтервал. Для варіанти, яка є на межі інтервалу, частоту ділять наполовину і вписують частину в попередній, а частину в наступний інтервал. Таблицю, в якій у першому рядку записані інтервали в порядку зростання (ці інтервали повинні накривати найбільше і найменше значення варіанти), а в другому – частоти або відносні частоти, називають інтервальним варіаційним рядом.
Інтервальний варіаційний ряд будують за даними спостережень ознаки, яка змінюється неперервно, а також ознаки, що змінюється дискретно, якщо обсяг вибірки достатньо великий.
Часто поряд з
поняттям частоти використовують поняття
накопиченої
частоти
![]() ,
яка показує, у скількох спостереженнях
ознака прийняла значення, менші від
заданого.
,
яка показує, у скількох спостереженнях
ознака прийняла значення, менші від
заданого.
При побудові інтервальних варіаційних рядів спочатку визначають величину інтервалу за формулою
![]() , (1)
, (1)
де
![]() і
і
![]() – відповідно найбільша та найменша
варіанти, n
– обсяг вибірки. Різницю в чисельнику
формули (1) називають розмахом
варіації.
– відповідно найбільша та найменша
варіанти, n
– обсяг вибірки. Різницю в чисельнику
формули (1) називають розмахом
варіації.
Якщо h
– дробове число, то за величину інтервалу
беруть найближче ціле число, або
найближчий нескладний дріб. Наприклад,
при
![]() ,
що знайдене за формулою (1), у випадку
великого розмаху варіації достатньо
взяти
,
що знайдене за формулою (1), у випадку
великого розмаху варіації достатньо
взяти
![]() ;
для малого розмаху – величину інтервалу
можна взяти
;
для малого розмаху – величину інтервалу
можна взяти
![]() .
.
У довільному випадку кількість інтервалів, що покривають найменше і найбільше значення варіанти, має бути близько , що є зручним для подальших досліджень варіаційного ряду (не варто будувати інтервальний ряд, наприклад зі інтервалами, оскільки це спричинює великі незручності для наступних досліджень його, а також – з двома, трьома інтервалами, бо це викликає великі похибки в наступних дослідженнях його та втрачається репрезентативність вибірки).
За початок першого
інтервалу зручно взяти
![]() ,
початок другого інтервалу збігається
з кінцем першого і дорівнює
,
початок другого інтервалу збігається
з кінцем першого і дорівнює
![]() ,
початок третього інтервалу збігається
з кінцем другого
,
початок третього інтервалу збігається
з кінцем другого
![]() .
Цей процес продовжують, поки початок
наступного інтервалу не буде більшим
від
.
.
Цей процес продовжують, поки початок
наступного інтервалу не буде більшим
від
.
Частоту
для кожного інтервалу (число значень,
що належать
-му
інтервалу) визначають як кількість
значень, що попадають в
-й
інтервал, причому ці значення можуть
збігатися з нижньою межею інтервалу,
але менші за верхню межу. Інколи визначають
середини інтервалів, які виконують роль
представників інтервалів
![]() .
Відносні частоти та щільність відносних
частот визначаються відповідно:
.
Відносні частоти та щільність відносних
частот визначаються відповідно:
![]() ;
;
![]() .
.
Дискретний варіаційний ряд записують у вигляді таблиці: у першому рядку записують значення варіант у порядку зростання або спадання, а в другому – частоти або відносні частоти :
|
|
|
… |
|
|
|
|
… |
|
|
|
|
… |
|
|
|
|
… |
|
Н
i
Інтервальний варіаційний ряд зображається гістограмою. Це ступінчаста фігура, яка складається з прямокутників, основами яких є інтервали варіаційного ряду довжиною , а висоти рівні частотам (відносним частотам) відповідного інтервалу. Інтервальний варіаційний ряд можна зображати і з допомогою полігонy. У цьому випадку інтервали замінюють їх серединами і до них відносять інтервальні частоти.
Характеристиками варіаційного ряду слугують перш за все середнє арифметичне, мода та медіана.
Середнє арифметичне варіаційного ряду обчислюють за формулою
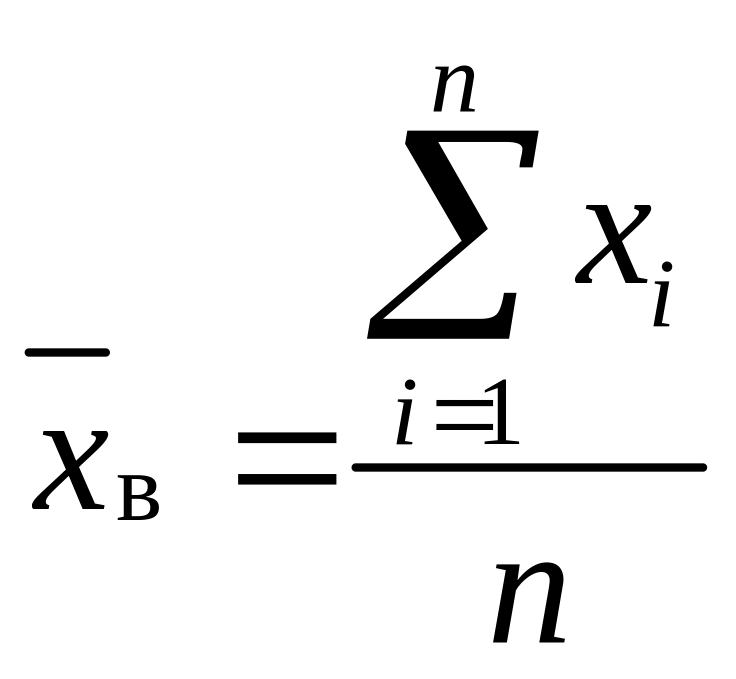 . (2)
. (2)
Якщо дані вибірки згруповані: варіанти записані в порядку зростання або спадання з відповідними частотами, то середнє арифметичне дорівнює
 (3)
(3)
де
– кількість груп, причому
![]() – обсяг вибірки.
– обсяг вибірки.
Середню арифметичну, обчислену за формулою (3), називають зваженою.
Зауваження 1.
Якщо початкові варіанти
– великі числа, то при обчисленні
вибіркової середньої зручно переходити
до умовних варіант
:
![]() ,
де
– число, близьке до вибіркової середньої,
взяте наближено. Тоді середнє значення
вибірки знаходиться за формулою
,
де
– число, близьке до вибіркової середньої,
взяте наближено. Тоді середнє значення
вибірки знаходиться за формулою
 . (4)
. (4)
Зауваження 2. Якщо всі результати спостережень зменшити (збільшити) в одне і те ж число разів, то середнє арифметичне зменшиться (збільшиться) у стільки ж разів.
Із цих зауважень випливає, що середнє арифметичне часто зручно обчислювати не для безпосередньо, а для умовних варіант:
![]() . (5)
. (5)
Знайшовши середню арифметичну для варіант , легко обчислити середню арифметичну для початкового варіаційного ряду:
![]() . (6)
. (6)
Медіаною
варіаційного ряду називають те значення
ознаки, яке припадає на середину
ранжированого ряду; її позначають
![]() .
Якщо кількість спостережень непарна
.
Якщо кількість спостережень непарна
![]() ,
то на середину ряду припадає
,
то на середину ряду припадає
![]() ,
тому
,
тому
![]() ,
якщо ж кількість спостережень парна
,
якщо ж кількість спостережень парна
![]() ,
тоді на середину ранжированого ряду
припадають два значення
,
тоді на середину ранжированого ряду
припадають два значення
![]() ,
тому
,
тому
![]() .
.
Для інтервального варіаційного ряду медіана визначається за формулою
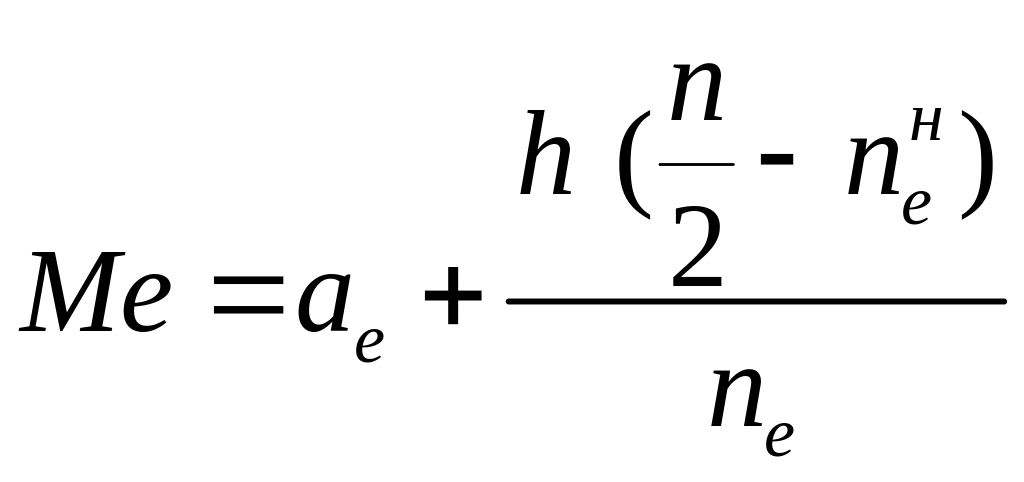 , (7)
, (7)
де
![]() початок медіанного інтервалу, тобто
такого, якому відповідає перша з
накопичених частот, рівна або більша
від половини всіх спостережень;
початок медіанного інтервалу, тобто
такого, якому відповідає перша з
накопичених частот, рівна або більша
від половини всіх спостережень;
![]() частота,
накопичена до початку медіанного
інтервалу;
частота,
накопичена до початку медіанного
інтервалу;
![]() частота
медіанного інтервалу.
частота
медіанного інтервалу.
Модою, для дискретного ряду, називається те значення варіанти, що має найбільшу частоту. Для інтервального варіаційного ряду моду визначають за формулою
![]() (8)
(8)
де
![]() початок
модального інтервалу, тобто такого,
якому відповідає найбільша частота;
початок
модального інтервалу, тобто такого,
якому відповідає найбільша частота;
![]() – частота модального інтервалу;
– частота модального інтервалу;
![]() частота
інтервалу, що передує модальному;
частота
інтервалу, що передує модальному;
![]() частота
інтервалу, наступного після модального.
частота
інтервалу, наступного після модального.
Емпіричною
функцією розподілу (функцією
розподілу вибірки) називають
![]() ,
яка визначає для кожного значення
відносну частоту події
,
яка визначає для кожного значення
відносну частоту події
![]() .
Вона знаходиться за формулою
.
Вона знаходиться за формулою
![]() , (9)
, (9)
де
![]() кількість варіант, що менші від
;
– обсяг вибірки.
кількість варіант, що менші від
;
– обсяг вибірки.
Властивості емпіричної функції розподілу:
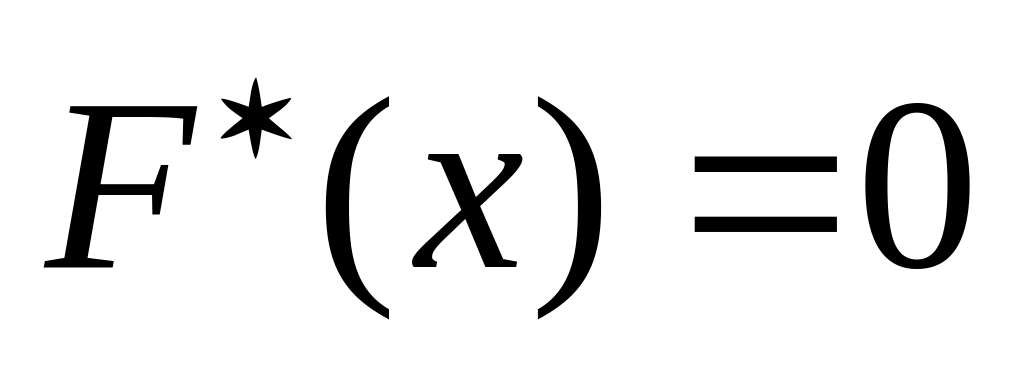 ,
при
,
при
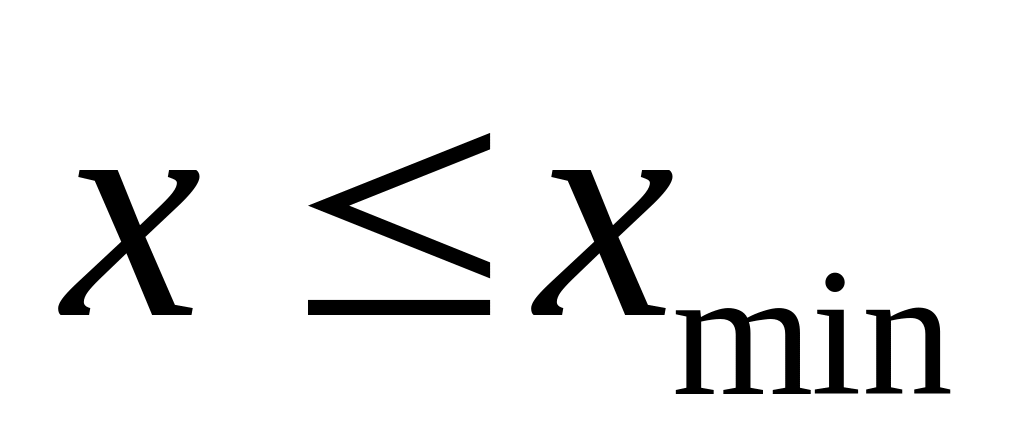 ;
;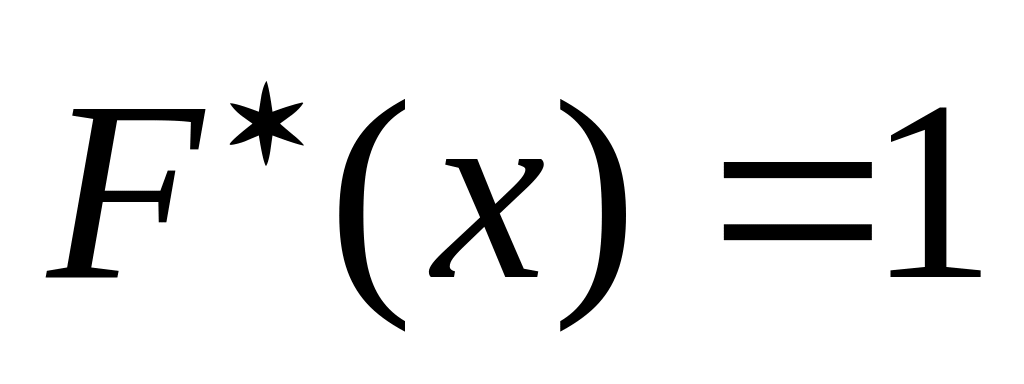 ,
при
,
при
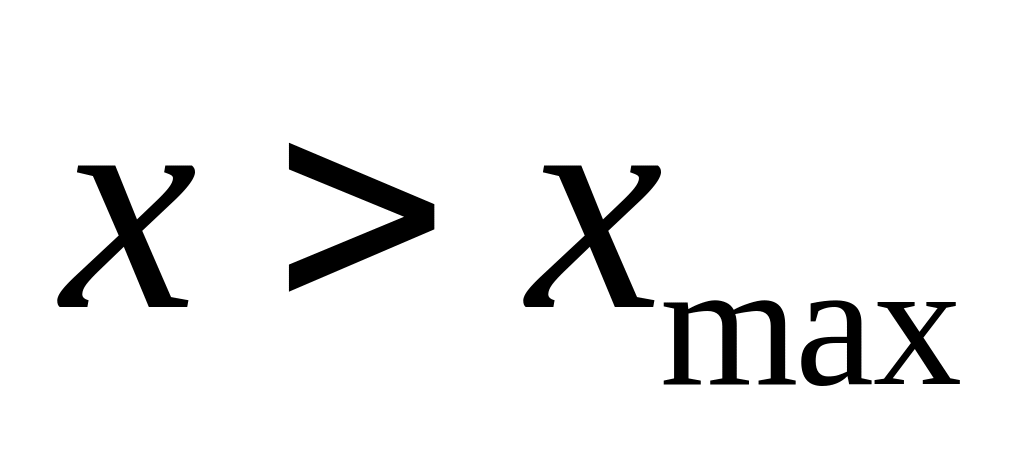 ;
;– неспадна функція.
Наприклад, для дискретного варіаційного ряду
|
|
|
|
|
|
|
|
|
|
емпірична функція розподілу має вигляд
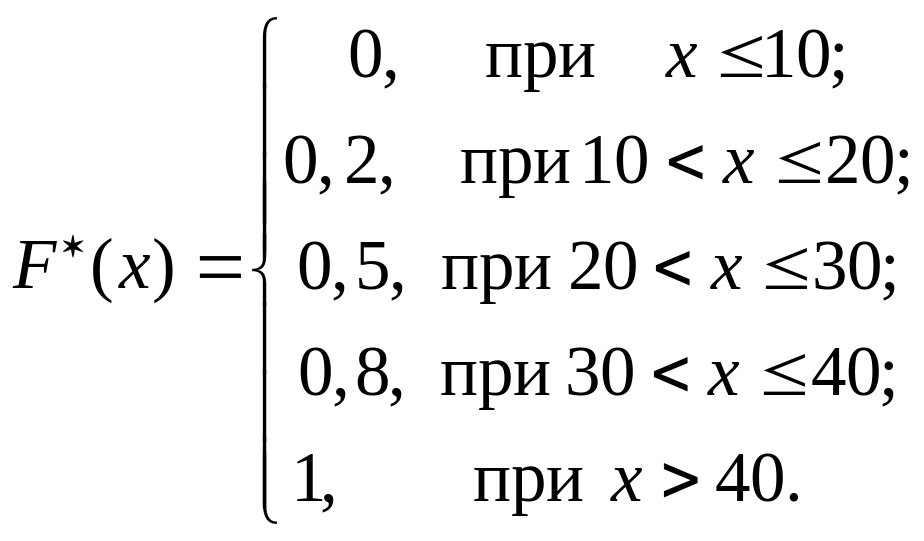
Виявляється, що за середнім арифметичним не можна судити про характер окремих відхилень від середньої величини. Часто важливо знати розмах коливань, тобто розмах варіації.
Варіаційний розмах – наближений показник варіації, оскільки він майже не залежить від зміни варіант, а крайні варіанти, які використовуються для його визначення, як правило, ненадійні.
Більш змістовними
є характеристики, які оцінюють розсіювання
значень випадкової величини навколо
середнього арифметичного. Оскільки
сума
![]() ,
то вона не може характеризувати варіацію,
тому розглядають або модулі, або квадрати
таких різниць.
,
то вона не може характеризувати варіацію,
тому розглядають або модулі, або квадрати
таких різниць.
Середнім лінійним відхиленням називають середню арифметичну абсолютних величин відхилень результатів спостережень від їх середньої
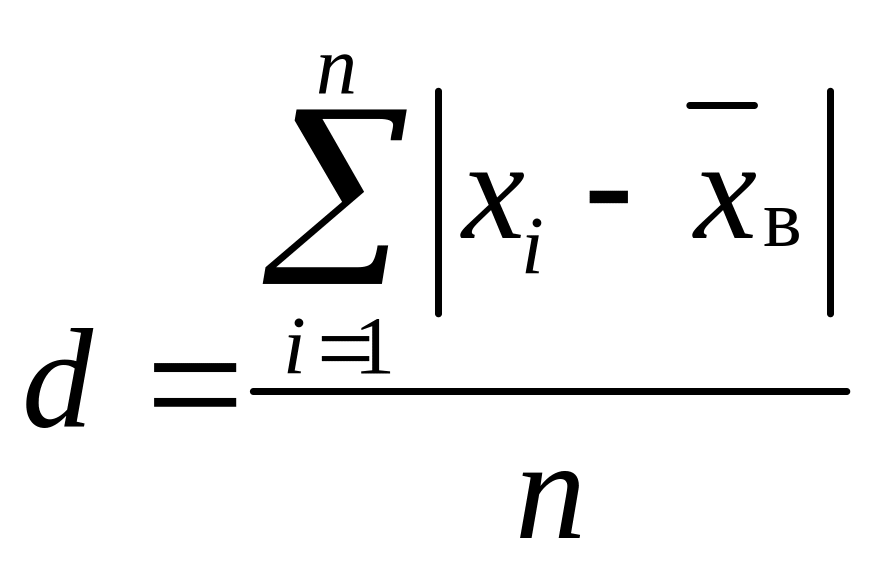 . (10)
. (10)
Для згрупованих даних формула (10) набуває вигляду
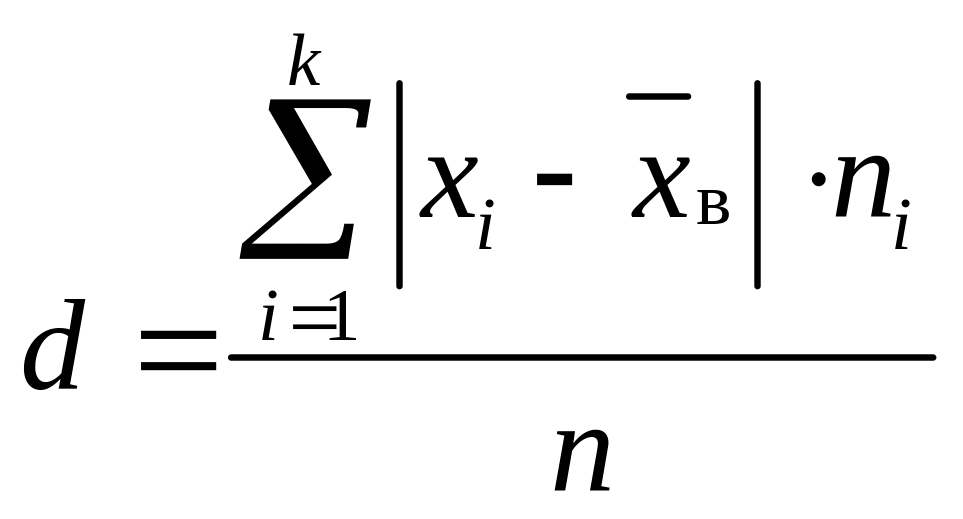 . (11)
. (11)
Вибіркова
дисперсія
![]() визначається за формулою
визначається за формулою
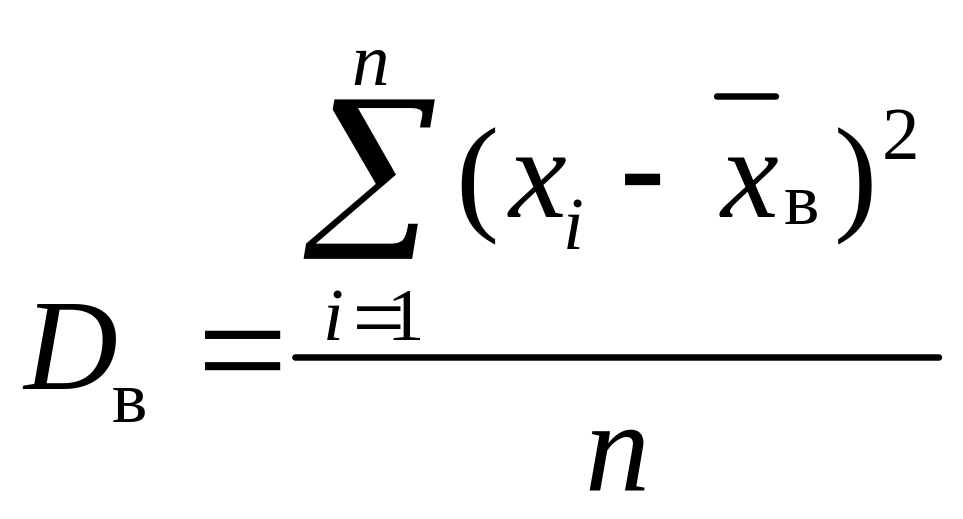 . (12)
. (12)
Для згрупованих даних дисперсія обчислюється так:
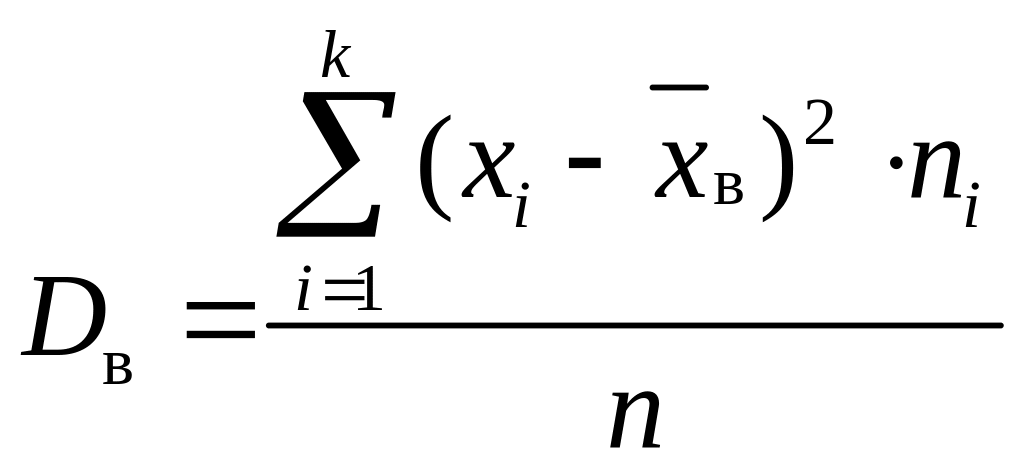 . (13)
. (13)
Проте зручною для обчислення дисперсії є формула
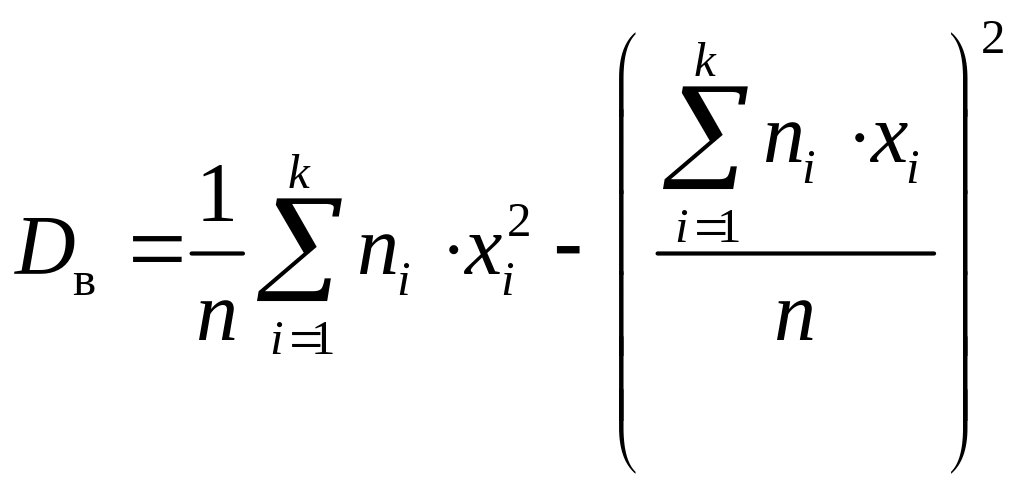 . (14)
. (14)
Замість дисперсії, за міру розсіювання спостережень навколо середньої арифметичної часто використовують середнє квадратичне відхилення, яке визначається за формулою
![]() (15)
(15)
і має ту саму розмірність, що й значення ознаки.
Відносною характеристикою варіації значень ознаки навколо середнього значення є коефіцієнт варіації, який обчислюється як відношення величини середньоквадратичного відхилення до середнього арифметичного значення за формулою
![]() , (16)
, (16)
де
![]() − виправлена вибіркова дисперсія.
− виправлена вибіркова дисперсія.
Зауваження 3.
Для спрощення обчислень, дисперсію
знаходять для варіант
![]() .
Тоді дисперсію для вихідного ряду можна
обчислити за формулою
.
Тоді дисперсію для вихідного ряду можна
обчислити за формулою
![]() . (17)
. (17)
Крім середнього арифметичного у якості середніх статистик використовується ще мода і медіана.
Якщо розподіл має
тільки одну вершину, то значення
,
для якого ця вершина досягається, є
модою
і позначається
![]() .
Якщо розподіл не дуже асиметричний, то
мода буде гарним наближенням “центра”
генеральної сукупності. Якщо мода
розподілу оцінюється за безліччю
згрупованих даних, то для знаходження
моди визначають групу з найбільшою
частотою. Ця група називається модальною.
Як моду беруть середнє значення цієї
групи. Значення
,
для якого
.
Якщо розподіл не дуже асиметричний, то
мода буде гарним наближенням “центра”
генеральної сукупності. Якщо мода
розподілу оцінюється за безліччю
згрупованих даних, то для знаходження
моди визначають групу з найбільшою
частотою. Ця група називається модальною.
Як моду беруть середнє значення цієї
групи. Значення
,
для якого
![]() безлічі спостережень лежить лівіше
цього значення, а
— правіше, називається медіаною
і позначається
безлічі спостережень лежить лівіше
цього значення, а
— правіше, називається медіаною
і позначається
![]() .
.
Приклади:
Знайти медіану вибірки {9, 3, 5, 8, 4, 11, 13).
Розв’язання.
Запишемо ранжирований ряд
3,4, 5, 8, 9,11,13.
Звідси
![]() .
.
Знайти медіану вибірки {1, 20, 9, 13, 4, 11}.
Розв’язання.
Ранжирований ряд 1, 4, 9.11, 13, 20, звідки
![]() .
.
Для подальшого важливо відзначити один з наслідків центральної граничної теореми.
Твердження
(наслідок
з центральної граничної теореми).
Якщо випадкова величина
підпорядкована нормальному закону
розподілу із параметрами
,
![]() ,
а
,
а
![]() —
ряд незалежних спостережень над
,
кожне з який має ті ж числові характеристики,
що й
,
тобто
—
ряд незалежних спостережень над
,
кожне з який має ті ж числові характеристики,
що й
,
тобто![]() ;
;
![]() то вибіркова
середня
то вибіркова
середня
![]() також підпорядковується нормальному
закону з параметрами
,
також підпорядковується нормальному
закону з параметрами
,
![]() .
.
