1.1.6. Обернена матриця

Матриця називається оберненою до матриці , якщо виконуються

рівності :

Якщо визначник матриці А не дорівнює нулю, то така матриця називається неособливою (невиродженою).

Теорема. Для того, щоб матриця мала обернену необхідно і досить, щоб вона була невиродженою.

Алгоритм знаходження оберненої матриці

для заданої квадратної матриці

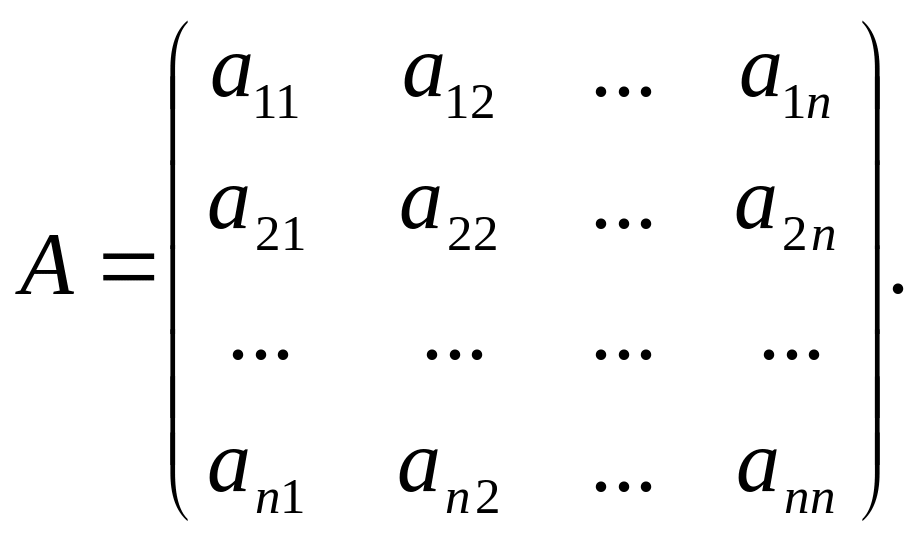
1.Знайти визначник матриці : .

2. Знайти алгебраїчні доповнення елементів матриці .

3. Скласти матрицю з алгебраїчних доповнень елементів матриці .

4. транспонувати матрицю з алгебраїчних доповнень. Ця матриця називається приєднаною (або союзною) і позначається .

5. Помножити приєднану матрицю на сило .

Отже, 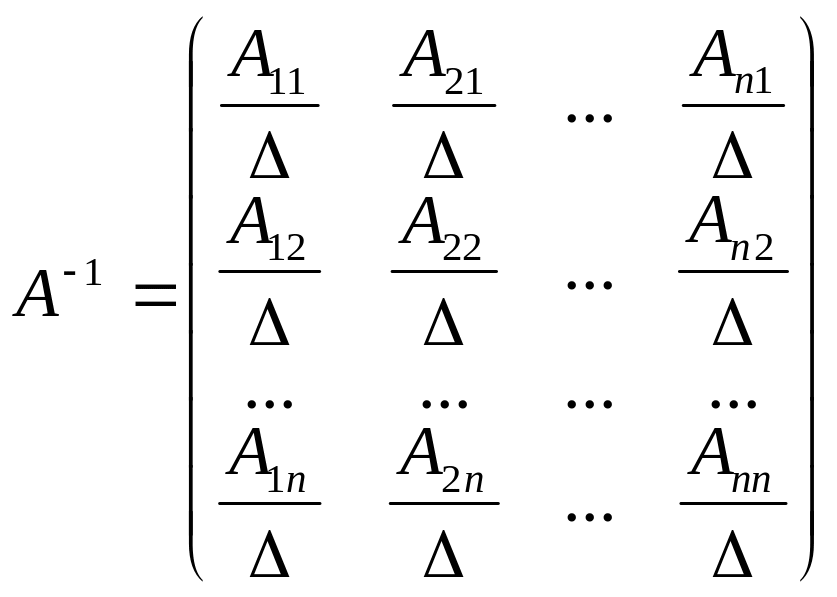- матриця, обернена до матриці .

Приклад 1.8. знайти матриця, обернену до матриці

.

Розв’язання

1. Знаходимо визначник матриці :

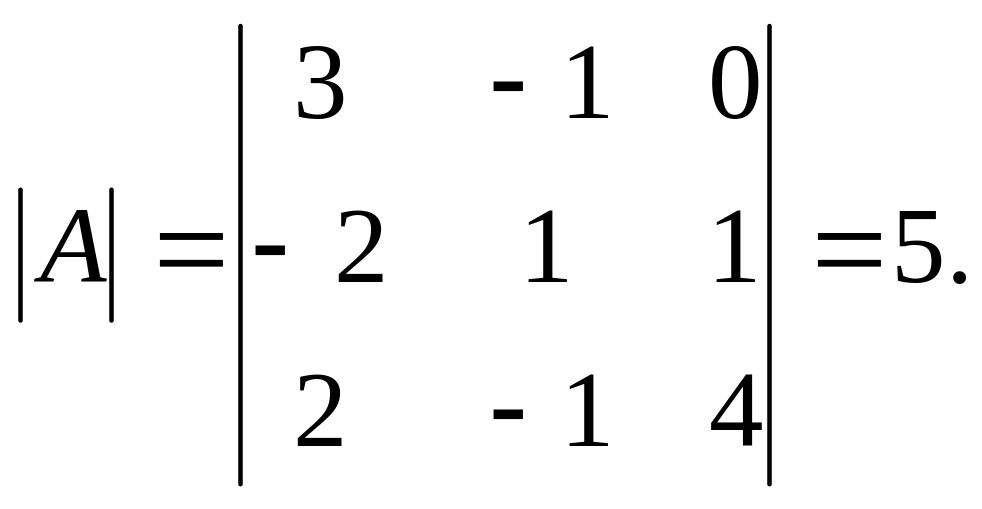
Оскільки , то обернена матриця існує.

2. Знаходимо алгебраїчні доповнення :

3. Так .

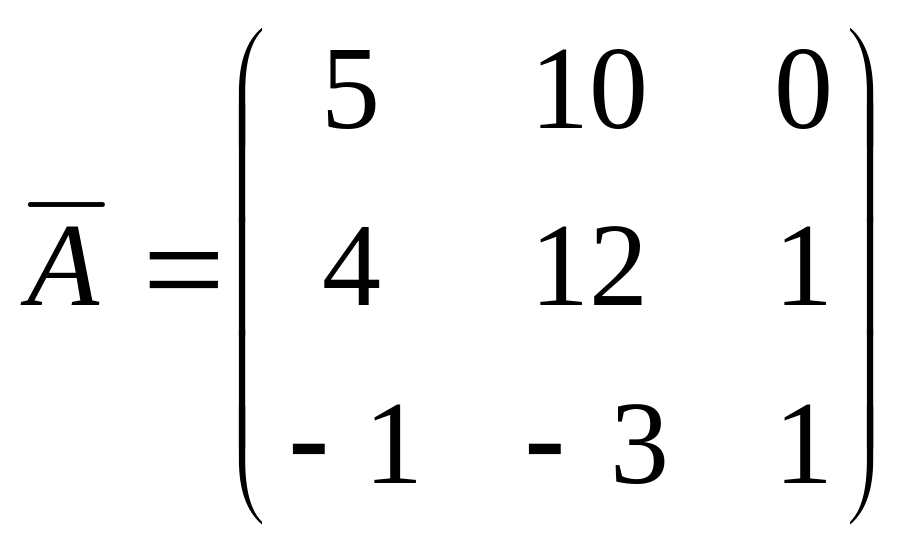4. Транспонуємо матрицю і знаходимо

.

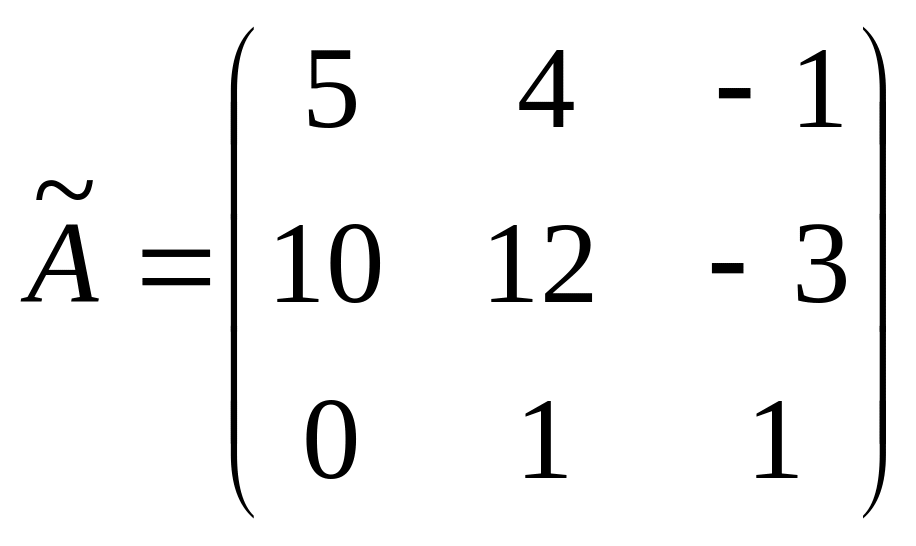5. Отже, обернена матриця .

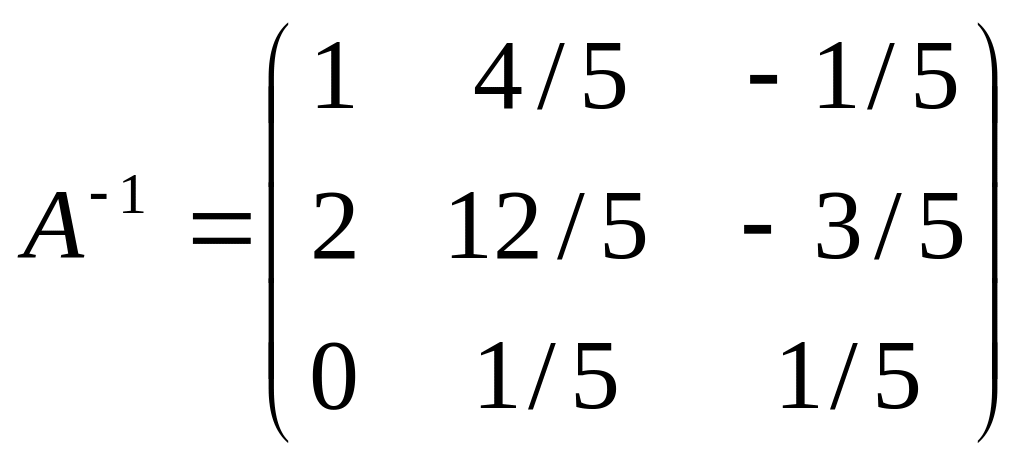Приклад 1.9. Знайти матрицю обернену до матриці

.

Розв’язання

1. обчислимо визначник матриці : .

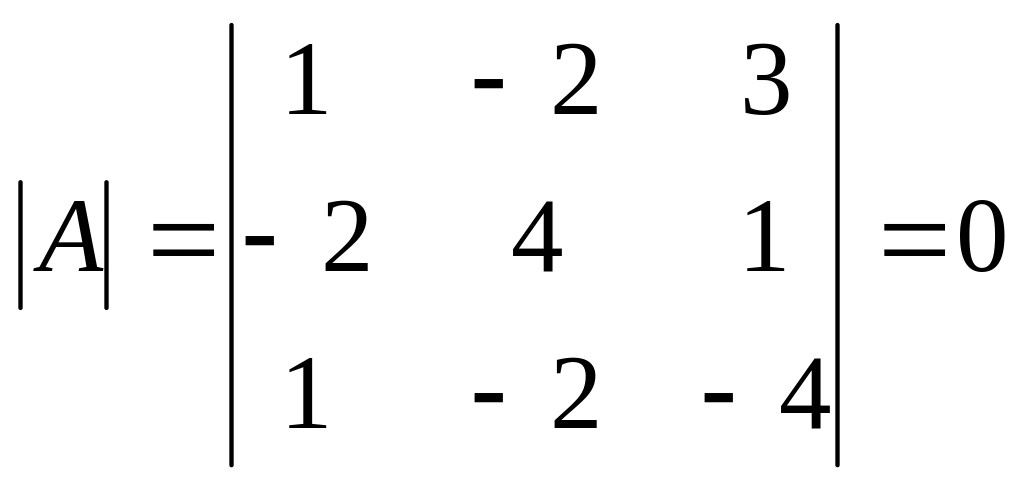Оскільки , то матриця вироджена, тобто оберненої для неї не існує.

1.1.7.Ранг матриці

Розглянемо прямокутну матрицю розміру : ,

Рангом матриці називається найвищий порядок мінора, що не дорівнює нулю.

Ціле число є рангом матриці , якщо серед її мінорів -го порядку є принаймні один, відмінний від нуля, а всі мінори, порядок яких більший, ніж дорівнюють нулю.

Властивості рангу матриці

1. ранг матриці порядку не перевищує меншого з чисел і , тобто .

2. тоді і тільки тоді, коли - нульова матриця.

3. Ранг квадратної матриці п-го порядку дорівнює п тоді і тільки тоді, коли матриця не вироджена, тобто її визначник не дорівнює нулю.

Методи обчислення рангу матриці

1. Метод окантування (за означенням).

2. Метод, який полягає в застосуванні елементарних перетворень матриці, до яких належать:

а) вилучення нульового рядка ( стовпця);

б) множення всіх елементів деякого рядка ( стовпця) матриці на число, відміне від нуля;

в) зміна порядку рядків(стовпців);

г) додавання до кожного елемента деякого рядка (стовпця);

ґ) відповідних елементів іншого рядка (стовпця), помножених на будь – яке число;

д) транспонування матриці.

З допомогою елементарних перетворень матрицю можна звести до трикутного вигляду.

Ранг матриці трикутного вигляду дорівнює кількості діагональних елементів, які не дорівнюють нулю.

Алгоритм знаходження рангу матриці

1. Зробити так, щоб коефіцієнт . Для цього можна поміняти рядки місцями.

2. В першому стовпці під коефіцієнтом зробити всі нулі. Для цього помножити перший рядок послідовно на 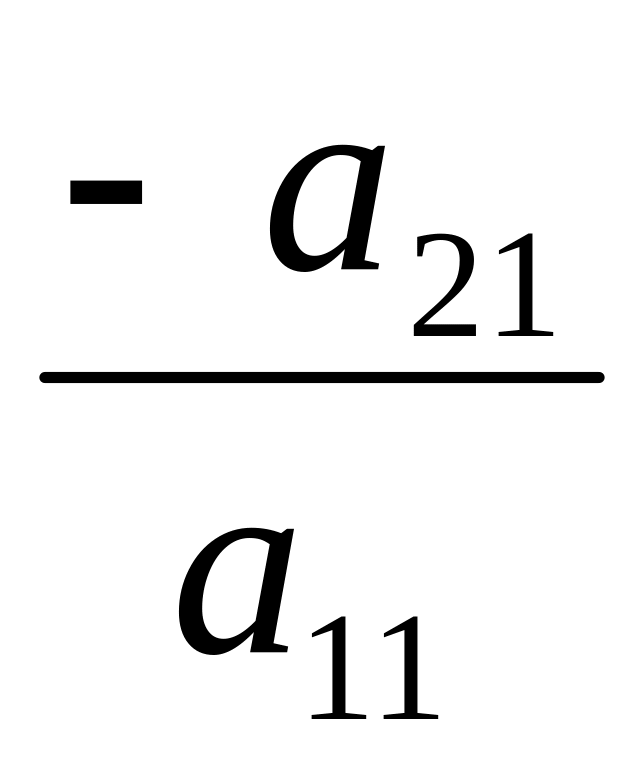, ,…, 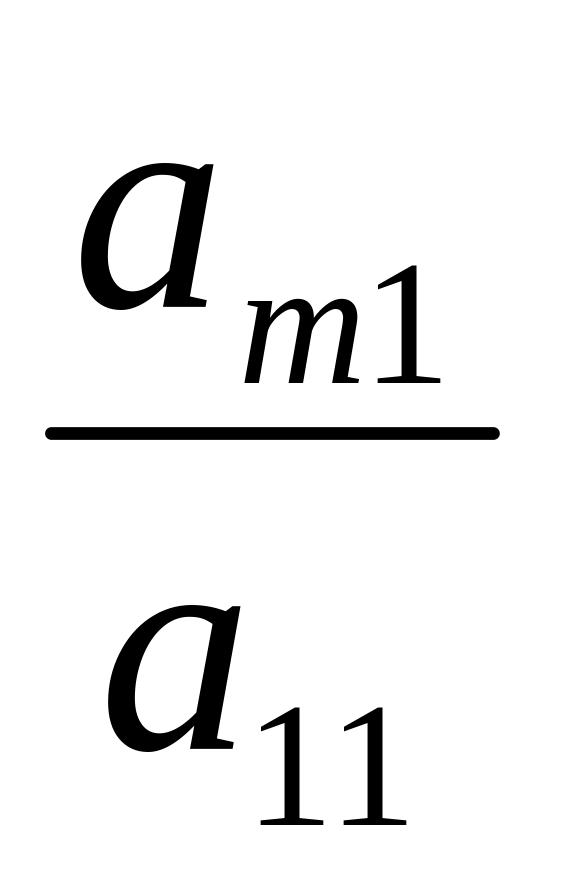і додати відповідно до другого, третього,…, т-го рядків.

3. Якщо в результаті перетворень отримали рядок чи стовпець, що містить усі нулі, то його вилучити.

4. Аналогічно зробити так, щоб коефіцієнт 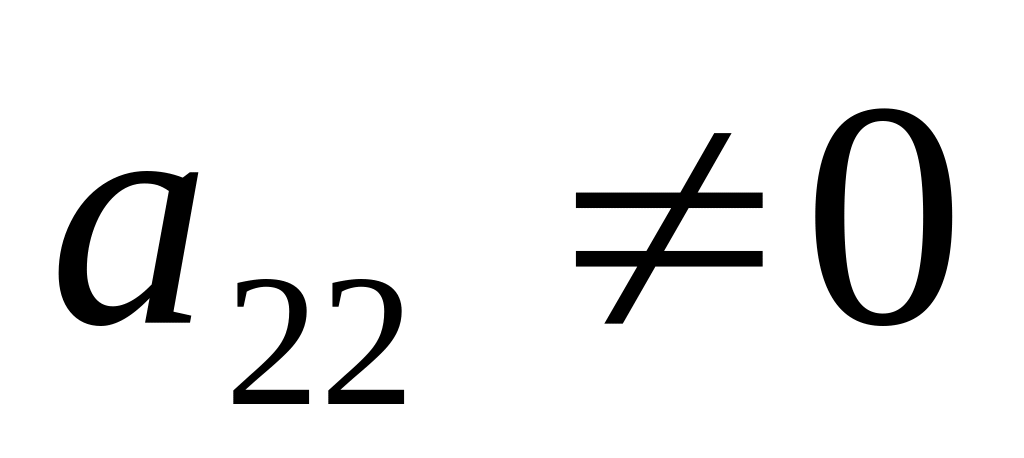, а під ним були нулі.

5. Описані дії повторити для всіх діагональних елементів (з однаковими індексами), доки матриця не буде зведена до трикутного вигляду.

6. Знайти ранг матриці (кількість діагональних елементів, які не дорівнюють нулю).

Приклад 1.10. Обчислити ранг матриці .

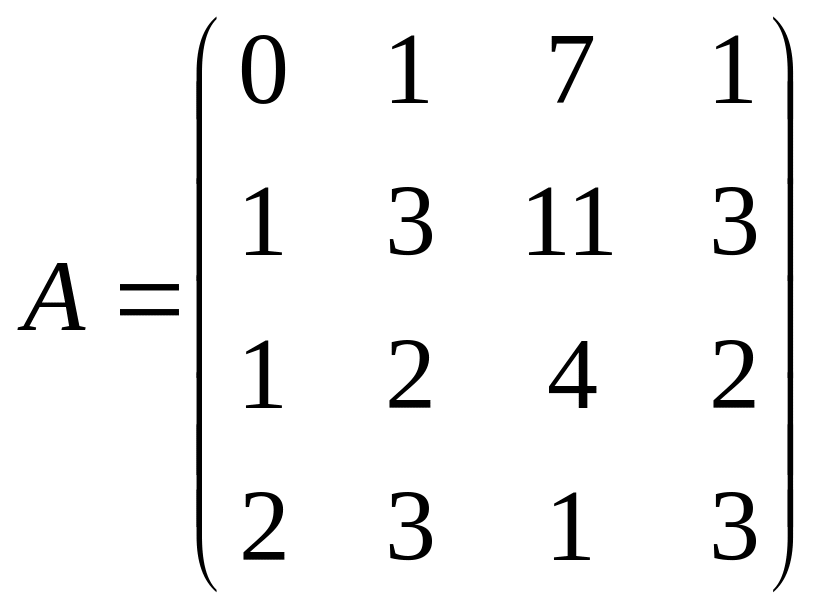Розв’язання

1. Поміняємо перший і другий ряд місцями для того, щоб елемент .

2. Щоб отримати в першому стовпці всі решта нулі, перший рядок домножимо на (-1) і додамо до третього рядка; перший рядок домножимо на (-2) і додамо до четвертого рядка;

3. Елемент . Щоб отримати нулі, другий рядок додамо до третього рядка; другий рядок домножимо на 3 і додамо до четвертого рядка;

4. Вилучимо нульові рядки.

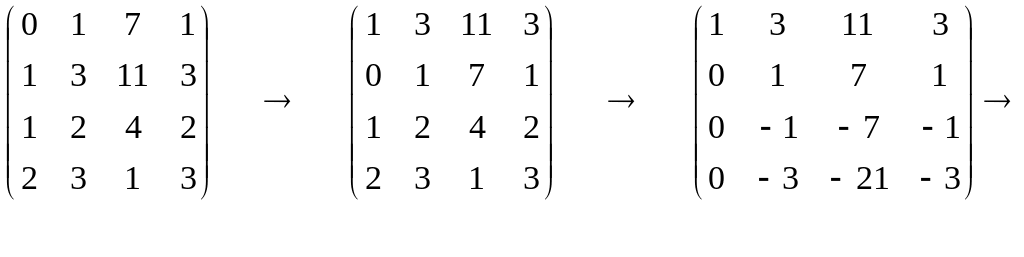
. Ранг матриці

Відповідь. .