
- •Розділ 1. Елементи лінійної алгебри
- •1.1.Елемнти теорії матриць та визначників
- •1.1.1. Поняття матриць. Види матриць
- •Види матриць
- •1.1.2. Дії над матрицями
- •Властивості дій над матрицями
- •1.1.3. Визначники другого та третього порядків
- •1.1.4. Основні властивості визначників
- •1.1.5. Визначники п-го порядку. Мінори та алгебраїчні доповнення
- •1.1.6. Обернена матриця
- •Алгоритм знаходження оберненої матриці
- •1.1.7.Ранг матриці
- •Властивості рангу матриці
- •Методи обчислення рангу матриці
- •Алгоритм знаходження рангу матриці
Розділ 1. Елементи лінійної алгебри
1.1.Елемнти теорії матриць та визначників
1.1.1. Поняття матриць. Види матриць
Прямокутна таблиця складена із довільного набору величин називається прямокутною матрицею. Величини, з яких складається матриця, називаються елементами матриці. Сукупність елементів, розміщених на горизонтальній (вертикальній) прямій складають рядок (стовпець) матриці.
Матриці позначаються великими латинськими літерами, а її елементи – малими латинськими з двома індексами, перший з яких вказує на номер рядка, а другий – на номер стовпця, на перетині яких цей елемент знаходиться.
Символічний добуток числа
рядків m
на число стовпців
n називають
розміром матриці і позначають
![]() .
.
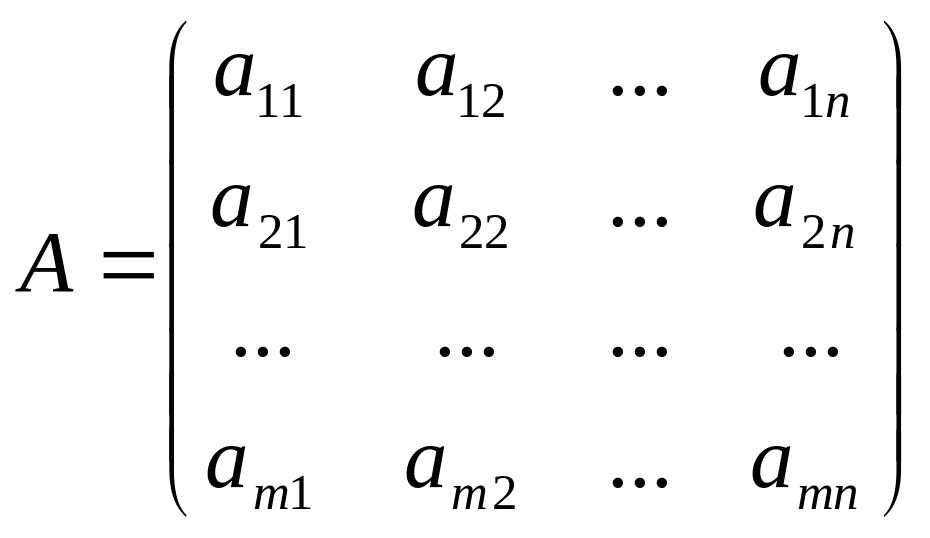 -
матриця розміру
.
-
матриця розміру
.
Скорочене позначення матриці
:
![]() .
.
Види матриць
Квадратна матриця – це матриця, в якій число рядків дорівнює числу стовпців. Кількість рядків ( стовпців ) квадратної матриці називається її порядком.
Наприклад ,
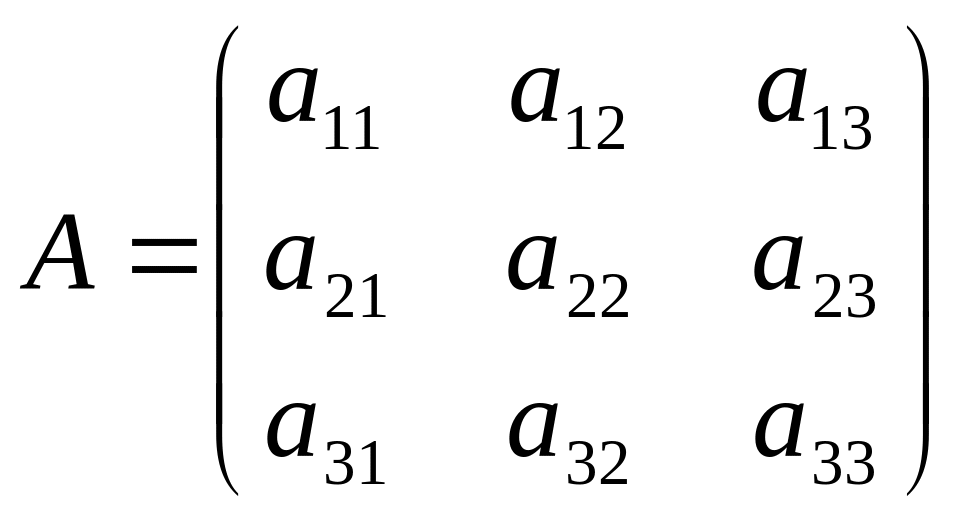 -
матриця 3-го порядку.
-
матриця 3-го порядку.
Елементи
![]() складають головну
діагональ матриці, а елементи
складають головну
діагональ матриці, а елементи
![]() утворюють побічну
діагональ матриці.
утворюють побічну
діагональ матриці.
Нульова ( нуль-матриця ) – це матриця, всі елементи якої дорівнюють нулю.
Діагональна – це квадратна матриця, всі елементи якої, крім діагональних, дорівнюють нулю.
Наприклад,
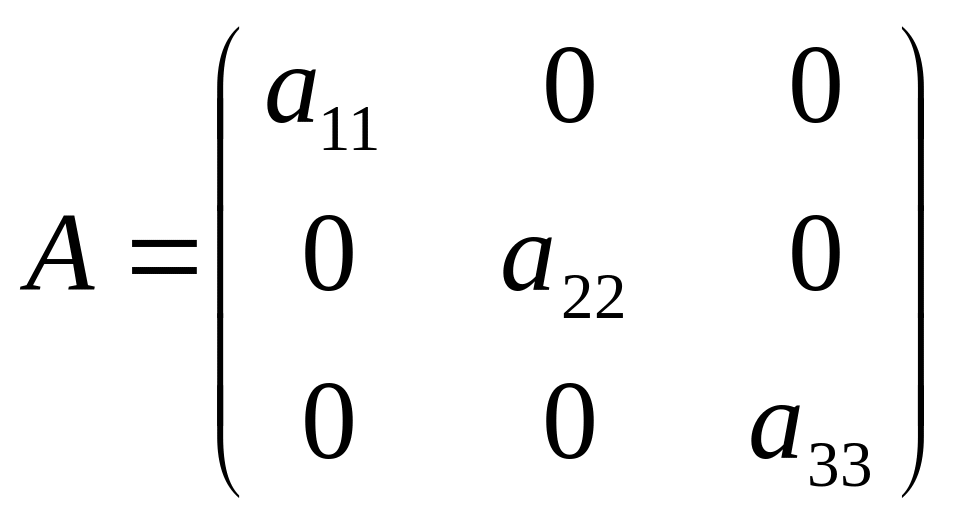 -
діагональна матриця 3-го порядку.
-
діагональна матриця 3-го порядку.
4. Одинична – це діагональна матриця, всі елементи головної діагоналі якої дорівнюють одиниці ( позначають Е ).
 -
одинична матриця 3-го порядку.
-
одинична матриця 3-го порядку.
5. Матриця-рядок ( матриця-стовпець) – це матриця, яка складається з одного рядка ( стовпця )
Наприклад,
![]() -
матриця-рядок,
-
матриця-рядок,
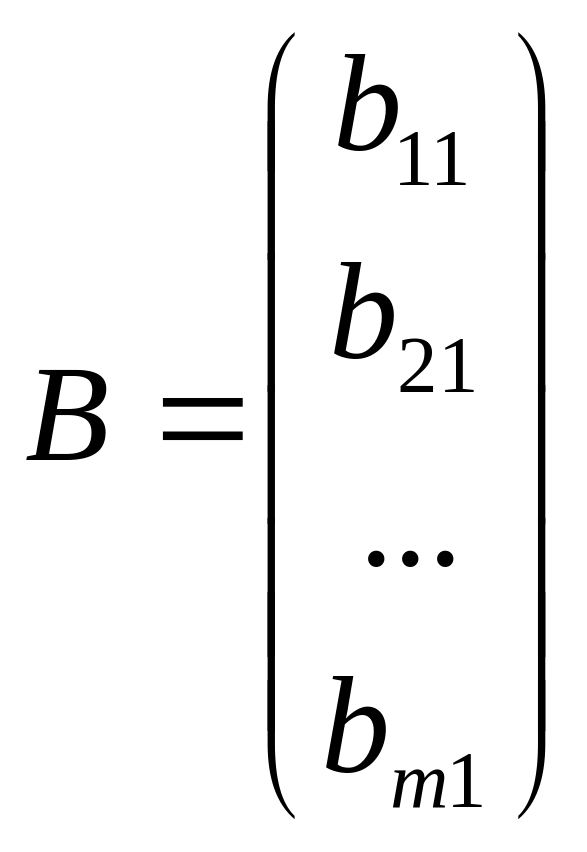 -
матриця-стовпець.
-
матриця-стовпець.
6. Трикутна – це матриця, в якої елементи, розміщені під головною діагоналлю, дорівнюють нулю.
7. Якщо у матриці А
замінити так, щоб 1-й рядок став першим
стовпцем, 2-й рядок став другим стовпцем
і т. д., то дістанемо матрицю, яка
називається транспонованою
відносно матриці А (
позначається
![]() ).
).
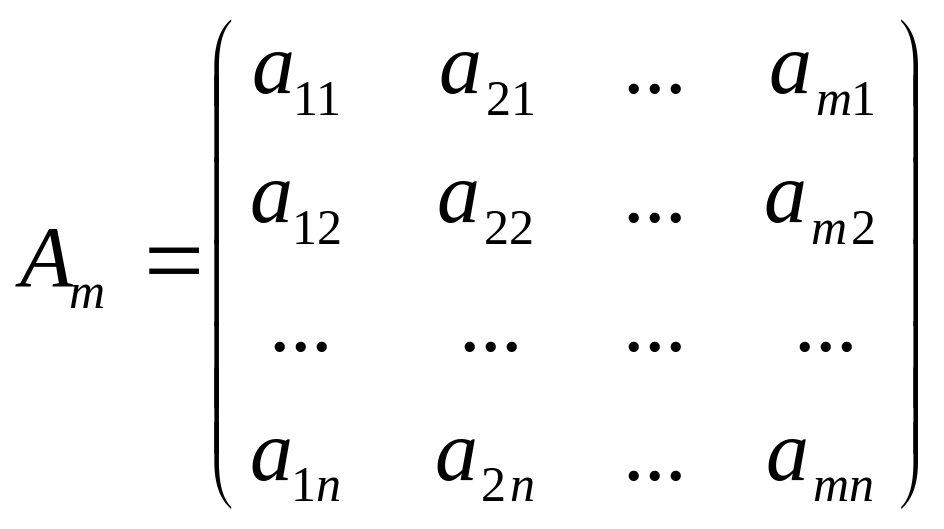 -
матриця, транспонована відносно А.
-
матриця, транспонована відносно А.
Перехід від А до називається операцією транспонування.
1.1.2. Дії над матрицями
Додавання та віднімання матриць. Сумою ( різницею ) двох матриць
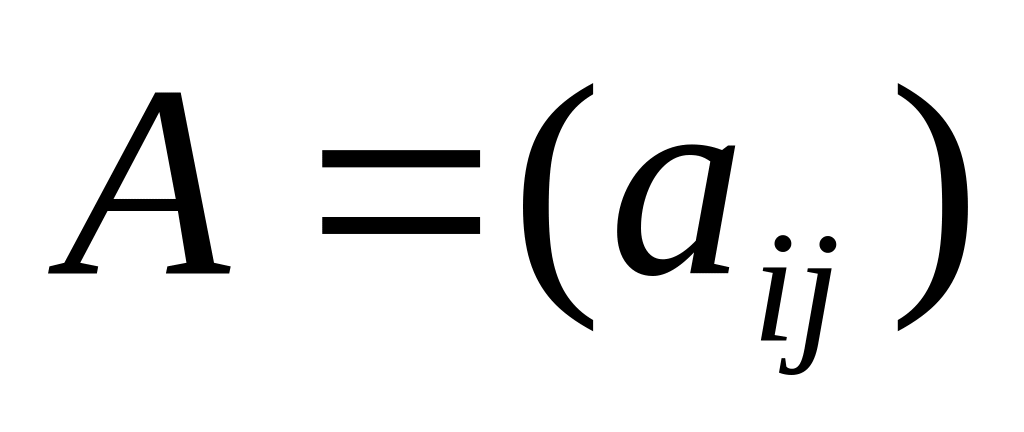 і
і
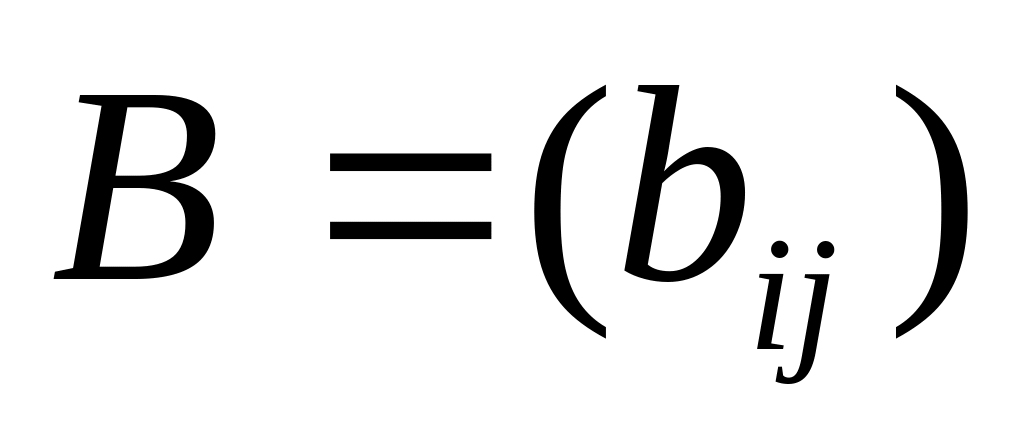 однакових
розмірів називається матриця С
такого самого розміру,
кожен елемент якої
однакових
розмірів називається матриця С
такого самого розміру,
кожен елемент якої
 дорівнює сумі ( різниці ) відповідних
елементів матриць А і
В тобто
дорівнює сумі ( різниці ) відповідних
елементів матриць А і
В тобто
|
Приклад 1.1. Нехай
![]() ,
,
![]() .
.
Знайти А-В.
Розв’язання
![]() .
.
Множення матриць на число. Добутком матриці на число
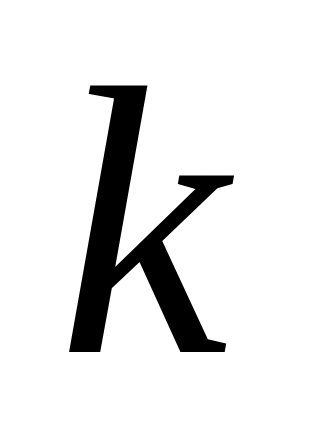 називається
матриця
називається
матриця
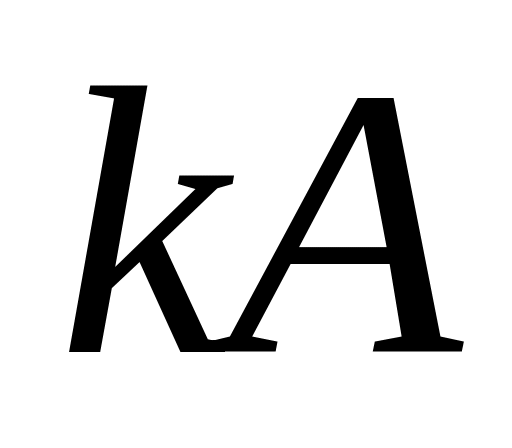 ,
елементами якої є добутки відповідних
елементів даної матриці на число
,
тобто
,
елементами якої є добутки відповідних
елементів даної матриці на число
,
тобто
|
,
![]() .
.
Наприклад,
якщо
,
то
![]() .
.
Множення матриць. Добутком матриць і з розмірами відповідно і
 називається матриця розміру
називається матриця розміру
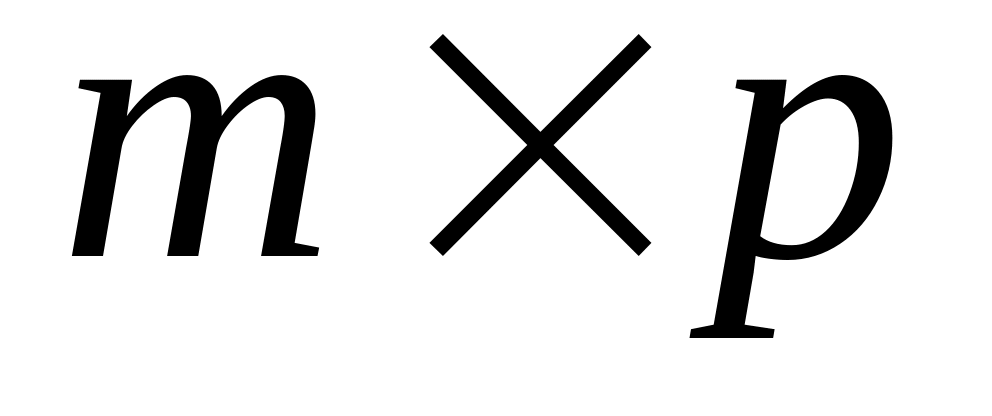 ,
кожен елемент якої
дорівнює сумі добутків елементів i-го
рядка матриці А на
відповідні елементи j-го
стовпця матриці В
, тобто
,
кожен елемент якої
дорівнює сумі добутків елементів i-го
рядка матриці А на
відповідні елементи j-го
стовпця матриці В
, тобто
|
Множити можна тільки узгоджені матриці, тобто ті, де число стовпців першої з матриць дорівнює числу рядків другої. Матриця-добуток при цьому матиме стільки рядків, скільки було у першій матриці, і стільки стовпців, скільки їх було у другій матриці.
Наприклад 1.2. Нехай
,
![]() .
.
Знайти
![]() .
.
Розв’язання
![]() .
.
