1 Идентификация объекта управления

1.1 Общая передаточная функция объекта регулирования

y_(p) x _(P)

_{Рисунок 1- Структурная схема объекта регулирования}

_{Структурная схема объекта регулирования представлена на рис.1 и описывается функцией :}

_{Wобщ(p)= Wo1 (р)*Wo2(р)*Wo3(р)*Wo4(р)}

_{0.6 0.7 2.6}

_{Wo1(p)= ------- ; Wo2(p)= -------- ; Wo3(p)= ------- ; W04(p)= e}^{- 2.2+1}

_{0.4р +1 2.4р +1 1.8р +1}

_Koi

_{Wi (p) = --------}

_{Toi + 1}

_{W04 (p)= e} ^{- p*I}

_{Структурная схема состоит из четырёх последовательно соединённых звеньев, где W01(p), W02(p) и W03(p) звенья инерционного первого порядка и W04(p) звена чистого запаздывания.}

_{Передаточная функция объекта и системы полностью определяет ёё динамические свойства и первоначальная задача расчёта}

_{АСР сводится к определению ёё передаточной функции. Вследсвии тoго что элементы объекта и системы обладают свойством}

_{детектирования передаточную функцию объекта можно найти по передаточным функциям отдельных его элементов :}

y_{(p) X (p)}

_{рисунок 2- Упрощённая модель объекта регулирования}

_{В этой структурной схеме я преобразовал} Wo­₁(p) c Wo­₂(p), по правилу эквивалентного преобразования, для упрощения со схемой. Передаточная функция всей схемы регулирования принципе не изменилась только два звена стали одним общим и их произведение равно общей передаточной функцией двух звеньев:

0.6 0.7 1.02

_{Wэкв (p) = Wo1(p)* Wo2(p)= -------- * ----------- =} --------------------

0.4р +1 2.4р + 1 9.84р² + 6.5 s + 1

y_(p) x _(P)

_{Рисунок 3 – Эквивалентная модель объекта регулирования}

_{И ещё раз упростили схему по правилу эквивалентного пребразования и совместили два звена и вид их общей передаточной}

_{функции будет выглядеть так:}

_{1.02 2.6 2.652}

_{Wэкв (p) = Wo1(p)* Wo2(p)= -------------------------- * ------------ = ------------------------------------------}

9.84р² + 6.5р + 1 1.8р + 1 17.712р³ + 21.54р² + 8.3 +1

y_(p) x _(P)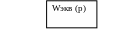

_{Рисунок 4 – Общая схема объекта регулирования}

_{Структурную схему преобразовали до того, что в ней осталось одно звено, а его передаточная функция равна произведению}

_{соединённых звеньев:}

_{0.6 0.7 2.6 - 2.652 + 0.92727}

_{Wэкв (p)=} ------- * ------- * -------- * e^{- 2.2 +1} = -------------------------------------------

0.4р+1 2.4р+1 1.8р+1 17.712р⁴+37.6418р³+27.8818р²+ 8.5455р + 0.90909

_{Независимо сколько раз я преобразовывал структурную схему общая передаточная функция остаётся неизменной.}

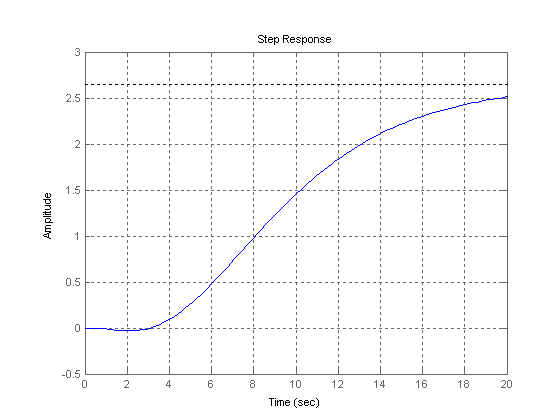
Рисунок 5

Кривая переходного процесса представлена на рис.2 Переходным процессом называют процесс перехода

выходного сигнала элемента из одного установившегося состояния в другое при поступлении на вход элемента ступенчатого сигнала. Графическое изображение переходных процессов подразделяются на

колебательные и монотонные. На данном рисунке изображен монотонный процесс, который имеет

S- образный характер изменения выходного сигнала

Функция построения графика переходного процесса описана программой MATLAB 6.1 и имеет вид

n1=[0.6];d1=[4.1 1];

n2=[1.7];d2=[2.4 1];

n3=[2.6];d3=[1.8 1];

[num1,den1]=pade(2.2,1);

[num2,den2]=series(n1,d1,n2,d2);

[num3,den3]=series(num2,den2,n3,d3);

[num4,den4]=series(num1,den1,num3,den3);

printsys(num4,den4);

step(num4,den4);

grid on