4. Класс nр - полных задач

Ниже излагаются основы теории сложности, заложенной в основополагающих работах С. Кука [7], Р. Карпа [8], А.А. Левина [9]. Важно обратить внимание на полиномиальное преобразование задач как главный элемент этой теории. Известно, например, что задача о максимальном потоке в сети может быть преобразована в задачу линейного программирования. Подобные преобразования задач иногда оказываются полезными для нахождения решений, и для их осуществления приходится производить некоторые вычисления, связанные с перекодированием начальной информации и

ответа - решения задачи (рис. 4.1).

Определение 4.1. Задачи множества Z полиномиально сводимы к задачам множества S (обозначение - Z S ), если существует функция  . вычисляемая за полиномиальное время и преобразующая любую задачу z Z в задачу (z) = s, s S , причем z Z  (z) S

Преобразо-вание за

полиноми-

альнов время

Алгоритм решения задачи

(z)

Преобразо-вание за

полиноми-

альнов время

Вход Вход Выход Выход

задачи задачи задачи задачи

Z (z) (z) Z

Рис. 4.3. Схема полиномиальной сводимости задачи Z к

задаче (z).

О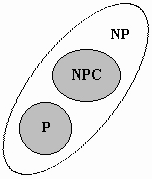 пределение 4.2. Задача Z* называется NР - полной (универсальной переборной задачей), если Z* NР и для любой задачи Z NР имеет место полиномиальная сводимость Z  Z*.

Множество всех NР- полных задач часто обозначают NPС (Nondeterministic Polinoyal Compete). Из определения 4.2. следует, что NPС NP и NP-полные задачи являются наиболее сложными в классе NP : если хотя бы одну NP-полную задачу удалось решить за полино-миальное время, то и все задачи из NP (в силу полиномиальной своди-мости Z  Z* ) также удалось бы решить за полиномиальное время.

Теорема 4.1 [1].

1)Если  , то  Р   Р;

2) Если  и  , то 

3) Если  NР,  NР,  NРС и  , то  NРС. Доказательство вытекает из определений 2.1, 3.1, 4.1 и 4.2.

Теорема 4.1 указывает способ доказательства. NР-полноты некоторой задачи Z, если известна хотя он одна NР-полная задача

Z*: достаточно доказать, что  NР и что Z* Z .

Изучение сложности дискретных задач началось с исследования задач вычисления (или распознавания) свойств. Эти задачи для допустимой начальной информации могут иметь решение, представ-ляющее собой ответ «да» или «нет» (1 или 0). Например, имеет ли данный конечный граф хотя бы один гамильтонов контур, является ли совместной система линейных неравенств с целочисленными переменными и тому подобные задачи. В последствии результаты исследования сложности задач вычисления свойств были распространены и на другие, в частности оптимизационные задачи.

Рис.4.2 Теоретико - множественная диаграмма класса NP в предположении

что P NP.