Исследование функций рождаемости, смертности, мальтузианской функции, фазового портрета популяции.
Рекомендации (практические) и ограничения.
Исследование выполняется методом математического моделирования динамики популяции на основе приведенных выше уравнений.
Моделирование выполняется с помощью программ, приведенных в приложении.
В учебной лаборатории программы стоят в субдиректории worc пакета программ МАТЛАБ 6.1.
Для работы на домашнем компьютере откопируйте программы в отдельные файлы, поместив их в субдиректорию worc указанной или иной, лучше одной из последующих версий МАТЛАБА.
Поскольку система команд всех версий пакета в основном едина, программы легко адаптировать к любой версии, начиная с 3.1.
Работа пользователя ограничивается вводом нужных значений указанных выше параметров, вызовом программ и выходом из режима пользования ими.
Другие изменения в программах в ходе выполнения лабораторных работ не разрешаются.
Перед работой создайте резервные копии программ, зафиксируйте начальные значения параметров, которые вы должны будете снова ввести в конце работы.
Для хранения своих результатов в лаборатории создайте свой файл или даже субдиректорию по адресу D:\students\(курс)\(группа)
Хотя расчеты выполняются в МАТЛАБЕ, оформление отчета о работе удобнее выполнять в текстовом редакторе WORD.
В начале каждого раздела работы освойте работу с программами.
Описание пограммы EL12Maltus.
Программа EL12Maltus предназначена для расчета и отображения
- функций рождаемости, смертности, мальтузианской функции,
- скорости изменения относительной численности популяции
- при заданных значениях параметров популяции,
- на заданном промежутке значений ее относительной численности,
- при заданном шаге вычислений.
Войдите в среду МАТЛАБ и с помощью меню «Файл» откройте программу.
Рассмотрите ее состав, использование команд.
В приводимых ниже строках ввода данных установлены промежуток и шаг расчетов, параметры популяции. Вы можете согласиться с введенными данными или изменить их по своему усмотрению.
Остальные строки программы в лаборатории изменять не разрешается, дома тоже лучше воздержаться от этого.
N=0:.1:5;
NChild=3; % стандарт - 3, варьируйте от 1 до 5;
Narc=.001; % стандарт - .001, варьируйте до .05-.1;
Commun=1.5; % >1, стандарт - 1.5;
QLife=1; % стандарт - 1, диапазон - от 0.5 до 1.5;
Contest=1.1; % стандарт - 1.1, диапазон - от 1 до 2.
Сохраните программу.
В рабочем окне МАТЛАБ-а
- наберите ее название EL12Maltus,
- получите графики функций рождаемости, смертности, мальтузианской функции (Рис.1).
После повторного нажатия на клавишу «Ввод» получите график скорости изменения относительной численности популяции в функции этой численности при заданных значениях параметров, то есть фазовый портрет популяции (Рис.2).
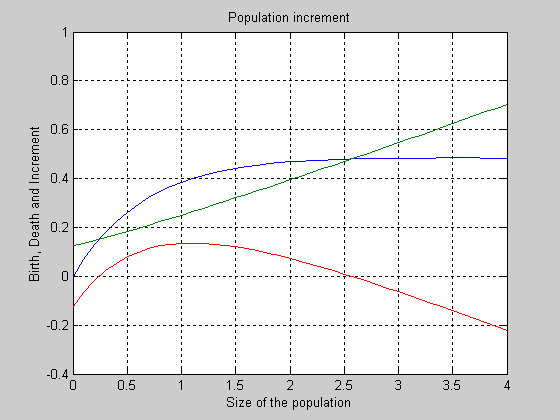
Рис. 1 Функции рождаемости, смертности, мальтузианская функция.
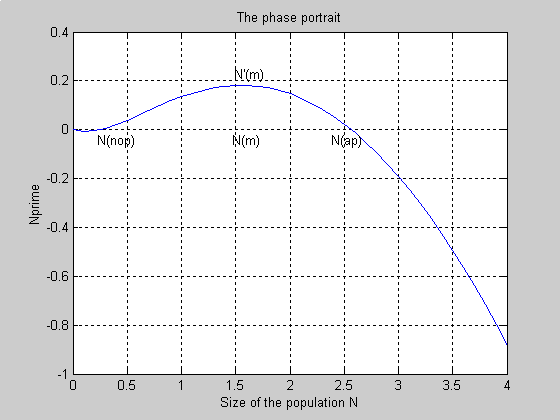
Рис. 2 Фазовый портрет популяции.
Оценка динамику популяции с помощью этих графиков (Рис. 1, 2).
Первой характеристикой этой динамики является факт наличия или отсутствия промежутка значений численности N, в котором N’ > 0, то есть популяция развивается.
При отсутствии такого промежутка популяция затухает, темп затухания будет лучше виден впоследствии на временном графике.
Но будем рассматривать в основном оптимистичные сценарии.
При наличии промежутка развития в качестве характеристик области и темпа развития используем следующие параметры фазового портрета (см. Рис. 2):
- N(пор) - пороговое значение относительной численности популяции, превышение которого
ведет к росту популяции, а недостижение которого - к ее затуханию;
- N’(m) - максимальный темп роста популяции,
- N(m) - относительная численность, при которой этот экстремум достигается,
- N(ар) - емкость ареала обитания популяции, относительная численность популяции, при
достижении которой меняется знак производной N’.
Рассмотрим вопрос об устойчивости стационарных точек фазовой плоскости с координатами (N(пор),0) и (N(ар),0).
Пусть в исходном состоянии N=N(пор), N’=0 (первая стационарная точка).
Пусть теперь по каким-то причинам
возникло малое отклонение
N
от N(пор) и
стало N=N(пор)+∆N.
При этом возникло и отклонение производной ∆N’. Как видно из графика на Рис. 2, последнее отклонение таково, что sign(∆N’)=sign(∆N).
Отклонение производной от N, имеющее один знак с отклонением N, приведет к дальнейшему росту (по модулю) этого отклонения.
Если исходное ∆N>0, то и ∆N’>0, и изображающая точка на фазовой кривой будет двигаться вправо до N=N(ар).
Если же исходное отклонение ∆N<0, то и ∆N’<0, и изображающая точка будет двигаться влево, к началу координат.
Таким образом, малые отклонения изображающей точки от стационарной точки (N(пор),0) ведут к дальнейшему нарастанию отклонений.
Следовательно, эта стационарная точка неустойчива.
Вторая стационарная точка (N(ар),0) устойчива.
Действительно, как видно из фазовой кривой, малое отклонение ∆N=N-N(ар) приводит к возникновению ненулевой производной ∆N’, такой, что sign(∆N’)=-sign(∆N).
Последнее предопределяет возврат изображающей точки к исходной стационарной.
Стационарные точки, будучи точками стабильности относительной численности популяции, разделяют ось этой численности на промежутки:
0<=N<N(пор) - промежуток затухания популяции до 0;
N(пор)<N<N(ар) - промежуток роста относительной численности популяции до N(ар);
N>N(ар) - промежуток затухания относительной численности популяции до N(ар).
Отметим, что ненулевые (отличные от начала координат) стационарные точки мальтузианской функции и фазового портрета совпадают.
Теперь перейдем непосредственно к другому исследованию: