7.2.3 Тест Глейзера.

Полагается, что м/у ср.квадратич.отклонением σ и величиной х имеется зависимость:

В связи с тем, что σε неизв., необх.использ.заменители этой величины, в его кач-ве предлагается использ.|εi|. Он будет характеризовать σε, хотя и не точно:

Процедура: задаемся величиной γ, вычисляем |ε|. Вычисляем величину Zi=xi. Исп.|ε| и величину Zi с пом.метода наим.квадратов,находим оценки m и ν. Выбираем из получ.ур-я те, у кот.велич.ν будет существенно отличаться от 0. Из найденного ур-я с ν отлич.от 0, выбир.то, у кот.наиб.велич.R². эта кривая и явл.искомым з-ном изм-я гетероскедастичности.

7.3 Методы устранения гетероскедастичности.

В основе устранения гетероскед-ти лежит усл.придания наблюдениям, располож.близко от линии регрессии, большего веса, а наблюд., лежащим сравнительно далеко от линии регрессии – меньший вес..

В основе лежит утверждение, что теор.дисперсия, если мы каждую случ.составляющую поделим на дисперсию (ср.квадр.отклон.ε), то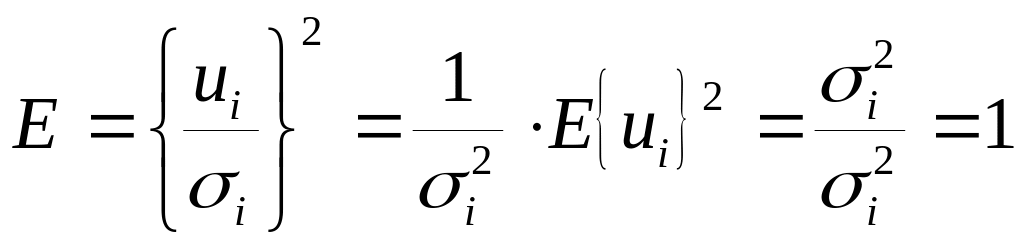

Если она =1, то гетероскед-ти нет: взвеш.ур-е регрессии, где σi – дисперсия случ.составляющей для i-го наблюдения.

В связи с тем, что σi не известна, находим такую переменную, кот.пропорциональна σi.

, гетероскедастичность можно устранить.

Нужно поделить на Z_i:

При выполнении теста Спирмена или Голдфенда-Квандта в качестве Zi использ.хi.

В случае если закономерность изм-я стандартных отклонений от факториального признака Х подчиняется более сложной завис-ти, обнаруживается с пом.теста Глейзера, для устранения гетероскедастичности в кач-ве Z_i берется теоретическое знач-е модуля εi.

8.1 Автокорреляция (остатков) и связанные с ней факторы.

При определ.ур-я регрессии значения случ.составляющей в любом наблюдении опред-ся независ.от его значений во всех др.наблюдениях. Автокор-ция – зависимость одной случ.составляющей от другой.

Последствия автокоррел.примерно такие же как и при гетероск-ти, т.е оценки коэф-тов ур-ия регрессии становятся неэффективными, стандартные ошибки коэф-тов ур-я занижаются. Обычно вопрос автокоррел.остатков возн.при исследов. временных рядов, но соседними значениями результирующего признака могут считаться знач-я, упорядоч-ые по возрастанию к.-л.факториальной переменной.

Постоянная направленность воздействия не включенного в ур-е регрессии к.-л.фактора явл.наиболее частой причиной положительной автокоррел. Случ.составляющая в ур.регрессии подвергается возд-ю тех переменных, влияющ.на у, кот.не вкл.в ур-е регрессии. Постоянная направленность возд-я не вкл.в ур.переменных, явл.обычной причиной положит.автокоррел.

Чем длиннее интервал м/у наблюдениями, тем меньше влияние автокоррел.

8.2. Обнаруж-е автокоррел.1-го порядка. Критерий Дарбина–Уотсона

Во многих случаях автокоррел.можно отразить в виде авторегрессионной схемы 1го порядка:

, где μt - некая случ.составляющая меньшаго порядка, чем Ut; ρ- коэф.автокоррел. , Если ρ= -1, то имеем отриц.автокоррел.; ρ=0 – автокоррел.отсутствует; ρ=1 - имеем положит.автокоррел. Из этого ур-я нельзя найти ρ, но его можно оценить с исп.МНК. При этом оценка:

Данный подход не дает ответа на вопр.какова стат.надежность найденной оценки ρ. Поэт.для оценкиавтокоррел.обычно исп.d-критерий Дарбина – Уотсона:

Для больших выборок dp≈2-2ρ, поэт.строится

Определ-ся масштабами наблюд-я. Они смогли дать критерий, где нах-ся d. Если dp<d2, то автокоррел.можно пренебречь, если dp<d1, то dp<dкр. – автокоррел.существенна.