1.6 Визначення відносних похибок

Порівняємо для положень механізму, які досліджуються, значення прискорень повзуна 5, що одержані методом планів і на діаграмах, прийнявши за основу результати, які одержані методом планів.

для 0-го положення механізму

де м/с²,

для 3-го положення механізму

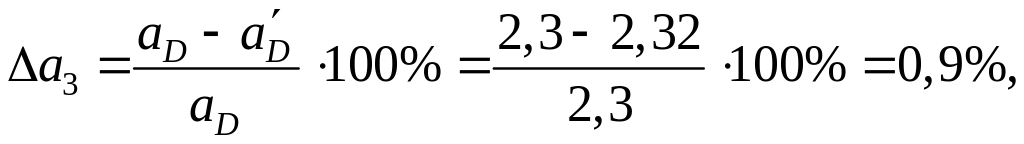
де м/с².

Одержані значення відносних похибок знаходяться у допустимих межах.

2. Кінетостатичне дослідження механізму преса

1. Визначення сили корисного опору

Силу корисого опору вивчаємо за заданою діаграмою . Викреслюємо цю діаграму в масштабі, показавши значення сил у відповідних положеннях механізму. Щоб полегшити розмітку осі абсцис цієї діаграми, відрізок вибираємо таким, що дорівнює максимальній ординаті діаграми .

Масштаб по осі ординат

Н/мм.

де - відрізок в мм, який зображає на діаграмі максимальне значення сили .

Відрізки по осі абсцис 0-1а, 0-1, 0-2, 0-3 і.т.д. діаграми дорівнюють ординатам , і т.д. діаграми .

Згідно із завданням сила діє постійно: при русі повзуна 5 вниз (в положеннях 1а-6).

2. Визначення сил інерції ланок

Сили інерції ланок визначаємо за формулою моменти сил інерції Знак “-” у цих формулах означає, що сила інерції напрямлена в протилежний бік прискоренню центра мас , а момент сили інерції в протилежний бік кутовому прискоренню

Тоді величини сил інерції ланок:

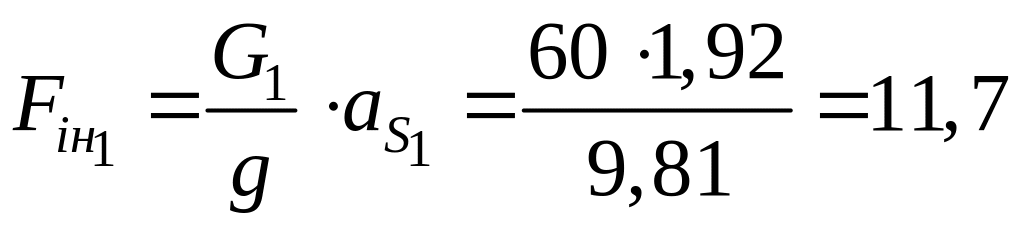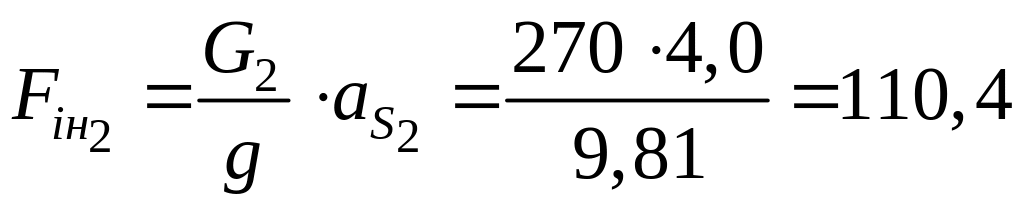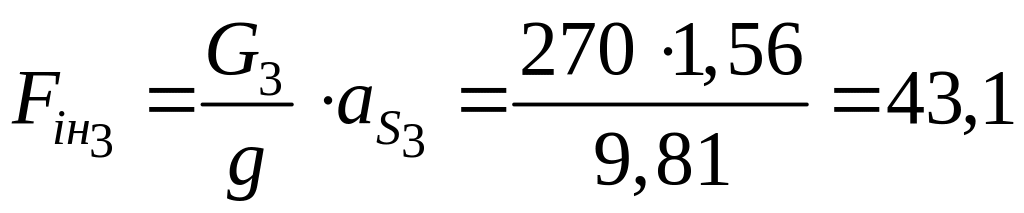Н;

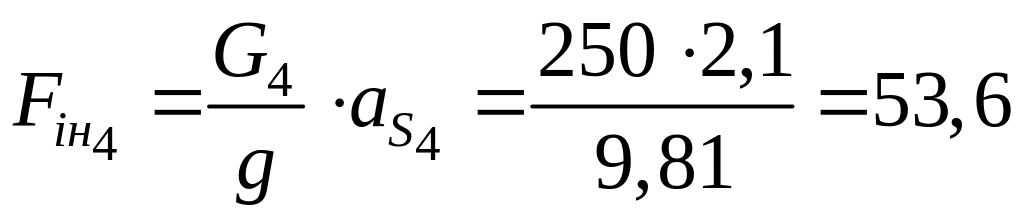Н;

Н;

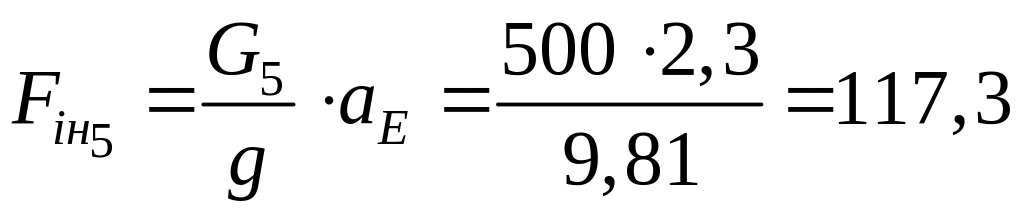Н;

Н.

Моменти сили інерції ланок 1,4,5 дорівнюють нулю, бо кутові прискорення цих ланок дорівнюють нулю.

Н/мм;

Н/мм;

Н/мм.

2. Силовий розрахунок групи 4-5

Визначення реакцій в кінематичних парах починаємо з групи 4-5. Викреслюємо групу 4-5 в масштабі м/мм. Прикладаємо до ланок 4 і 5 всі зовнішні сили включаючи сили інерції, дію ланок 0 і 3 замінюємо реакціями і .

Напрям реакції відомий (реакція напрямлена перпендикулярно осі руху повзуна 5, прикладаємо її в довільній точці). Реакцію прикладаємо в точці В, напрям її невідомий. Тому розкладаємо її на дві складові відносно осі ланки BD:

.

Для визначення дотичної складової складаємо рівняння моментів сил, що діють на ланку 4, відносно точки D:

,

де м, м.

Тоді

Н.

Складаємо рівняння рівноваги групи під дією всіх прикладених сил:

.

Будуємо план сил у масштабі Н/мм і знаходимо невідомі реакції:

Н;

Н.

Для визначення реакції в шарнірі D складаємо рівняння рівноваги ланки 4 під дією всіх прикладених до неї сил

.

На побудованому плані сил з’єднуємо кінець вектора з початком вектора , це і буде вектор :

Н.

2.4 Силовий розрахунок групи 2-3

На ланки цієї групи, крім сил тяжіння і , сил інерції і , моментів інерції і , діють ще реакції та зовнішня реакція яка прикладена в точці В і за величиною дорівнює , але направлена протилежно.

Реакції проходять, відповідно, через центри шарнірів А і С, їх напрями та величини не відомі.

Викреслюємо групу 2-3 в масштабі м/мм. Прикладаємо до ланок 2 і 3 всі зовнішні сили, включаючи сили інерції, дію ланок 1 і 0 замінюємо реакціями .

Для визначення реакцій розкладаємо їх на нормальні та дотичні складові:

і .

Для визначення реакції складаємо векторне рівняння суми моментів сил, що діють на ланку 2, відносно точки В:

.

Тоді

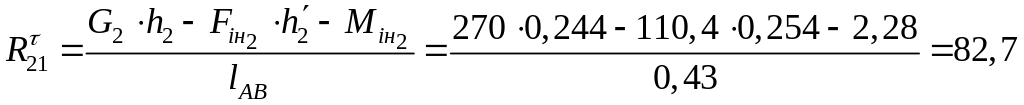Н.

Аналогічно знаходимо реакцію з рівняння моментів сил, що діють на ланку 3, відносно точки В:

.

Тоді

Складаємо рівняння рівноваги групи 2-3 під дією всіх прикладених сил:

В рівнянні тільки два невідомих отже рівняння розв‘язується методом плану сил. За цим рівнянням будуємо план сил у масштабі Н/мм і визначаємо невідомі реакції:

Н,

Н.

Для визначення реакції в шарнірі В між ланками 2 і 3 складаємо рівняння рівноваги ланки 2:

.

На плані сил з’єднуємо кінець вектора з початком вектора .

Реакція в шарнірі В:

Н.