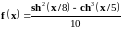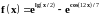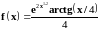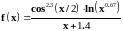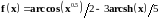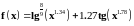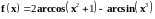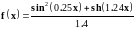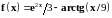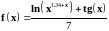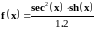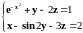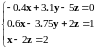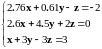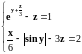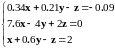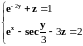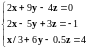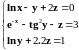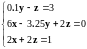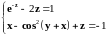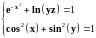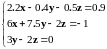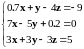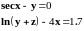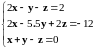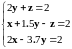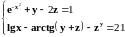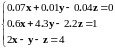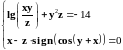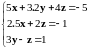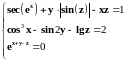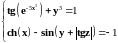2 Блок завдання функції matlab Fcn
Призначення: Визначає вираження в стилі мови програмування MATLAB.
Параметри:
• MATLAB function - Вираз мовою MATLAB.
• Output dimensions - Розмірність вихідного сигналу. Значення параметра -1 (мінус один) наказує блоку визначати розмірність автоматично.
• Output signal type - Тип вихідного сигналу. Вибирається зі списку:
1 real - Дійсний сигнал.
2 complex - Комплексний сигнал.
3 auto - Автоматичне визначення типу сигналу.
• Collapse 2-D results to 1-D - Перетворення двовимірного вихідного сигналу до одномерному.
Вхідний сигнал у вираженні позначається і, якщо він є скаляром. Якщо вхідний сигнал - вектор, необхідно вказувати номер елемента вектора в круглих дужках. Наприклад, u(1) та u(3) - перший і третій елементи вхідного вектора. Якщо вираз складається з однієї функції, то її можна поставити без вказівки параметрів. Вираз може містити також власні функції користувача, написані на мові MATLAB і оформлені у вигляді М-файлів. Ім'я м-файлу не повинне збігатися з ім'ям моделі (mdl -файлом).
Рисунок 18 демонструє застосування блоку MATLAB Fcn. У прикладі використовується функція My_Matlab_Fcn_1, що обчислює суму і твір двох елементів вхідного вектора. Текст функції (файл My_Matlab_Fcn_1.m) наведено нижче:
Функція у = My_Matlab_Fcn_1 (х, к);
y(1)=x*k;
y(2)=x + k;
Вираз для виклику функції, заданий параметром MATLAB function, має вигляд: My_Matlab_Fcn_1(u(1),u(2)) .
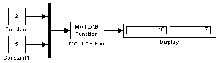
Рисунок 18 - Приклади використання блоку MATLAB Fcn
Завдання для виконання роботи
Завдання № 1. Побудувати графіки функцій у декартовій системі координат. Функції вибрати з таблиці 2 відповідно до свого варіанту. Результати представити у вигляді графіка.
Таблиця 2
Варіанти завдань
№ варианту |
Функція |
Діапазон вимірювання аргументу, шаг |
1 |
|
0 – 14, 0.5 |
2 |
|
0 –2π, π/20 |
3 |
|
0–2, 0.02 |
4 |
|
0 –2π, π/20 |
5 |
|
0.1 –1.8, 1/20 |
6 |
|
0.15 –3.8, 0.02 |
7 |
|
0–3, 0.02 |
8 |
|
0 –π, π/30 |
9 |
|
0 – 1.5, 0.15 |
10 |
|
0 –π/4, π/60 |
11 |
|
0 – 1.5, 0.03 |
12 |
|
0 – 5, 0.05 |
13 |
|
0 –3π, π/10 |
14 |
|
0 – 4.5, 0.06 |
15 |
|
0 –π, π/10 |
Завдання № 2. Вирішити системи лінійних і нелінійних рівнянь згідно свого варіанту. Варіанти завдань приведені в табл.3.
Таблиця 3
Варіанти завдань
№ варианта |
Линейное уравнение |
Нелинейное уравнение |
Начальные условия |
1 |
|
|
X0=-2 Y0=2 Z0=-1 |
2 |
|
|
X0=-1 Y0=1 Z0=-1 |
3 |
|
|
X0=0 Y0=2 Z0=1 |
4 |
|
|
X0=-2 Y0=0 Z0=-1 |
5 |
|
|
X0=-1 Y0=2 Z0=0 |
6 |
|
|
X0=-3 Y0=4 Z0=-1 |
7 |
|
|
X0=-4 Y0=1 Z0=0 |
8 |
|
|
X0=-2 Y0=0 Z0=0 |
9 |
|
|
X0=2 Y0=0 Z0=1 |
10 |
|
|
X0=1 Y0=2 Z0=0 |
11 |
|
|
X0=-2 Y0=-2 Z0=-1 |
12 |
|
|
X0=4 Y0=-7 Z0=-1 |
13 |
|
|
X0=-5 Y0=0 Z0=-1 |
14 |
|
|
X0=0 Y0=0 Z0=-1 |
15 |
|
|
X0=0 Y0=0 Z0=0 |
