12 Блок обчислення комплексного числа за його дійсної та уявної частини Real-Imag to Complex

Призначення: Обчислює комплексне число за його дійсної та уявної частини.

Параметри:

• Input - Вхідний сигнал (вибирається зі списку):

- Real - Дійсна частина.

- Image - Уявна частина.

- RealAndImage - Дійсна і уявна частина.

• Image part - Уявна частина. Параметр доступний, якщо параметр вхідного оголошений як Real.

• Real part - Дійсна частина. Параметр доступний, якщо параметр Input оголошений як Image

Вхідні сигнали блоку можуть бути скалярними, векторними або матричними. Параметри зображення Image part и Real part повинні задаватися як вектори або матриці, якщо вхідний сигнал є вектором або матрицею.

Приклади використання блоку Real-Imag to Complex показані на ріс.13.

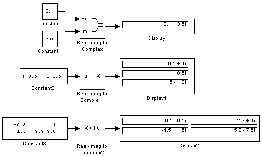
Рисунок 13 - Приклади використання блоку реальному уявної в комплексі

13 Блок обчислення комплексного числа за його модулю і аргументу Magnitude-Angle to Complex

Призначення: Обчислює комплексне число за його модулю і аргументу.

Параметри:

• Input - Вхідний сигнал (вибирається зі списку):

1 Magnitude - Модуль.

2 Angle - Аргумент.

3 MagnitudeAndAngle - Модуль і аргумент.

• Angle - Аргумент. Параметр доступний, якщо параметр оголошений як Magnitude.

• Magnitude - Модуль. Параметр доступний, якщо параметр оголошений як Angle.

Вхідні сигнали блоку можуть бути скалярними, векторними або матричними.

Параметри Angle і Magnitude повинні задаватися як вектори або матриці, якщо вхідний сигнал є вектором або матрицею.

Приклади використання блоку Magnitude-Angle to Complex показані на рис.14.

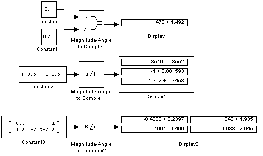
Рисунок 14-Приклади використання блоку Magnitude-Angle to Complex

14 Блок алгебраїчного контуру Algebraic Constraint

Призначення: Виконує пошук коренів алгебраїчних рівнянь.

Параметри:

• Initial guess - Початкове значення вихідного сигналу.

Блок знаходить таке значення вихідного сигналу, при якому значення вхідного сигналу стає рівним нулю. При цьому вхідний сигнал повинен бути прямо або опосередковано пов'язаний з вхідним сигналом.

На рис.15 показаний приклад вирішення системи нелінійних рівнянь виду:

.

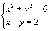
Оскільки дана система рівнянь має два рішення, то початкові значення блоків Algebraic Constraint задані у вигляді векторів. Для першого (верхнього) блоку початкове значення задано вектором [1 -1], а для другого (нижнього) блоку - вектором [-1 1].

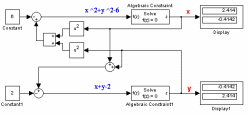
Рисунок 15 - Приклад використання блоку алгебраїчних обмежень

Блок Algebraic Constraint може використовуватися також і для вирішення нелінійних матричних рівнянь. На Рисунок. 16 показаний приклад вирішення нелінійного матричного рівняння виду:

.

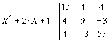
Рисунок 16-Приклад використання блоку алгебраїчних обмежень для вирішення нелінійного матричного рівняння.

Блоки функцій

1 Блок завдання функції Fcn

Призначення: Визначає вираження в стилі мови програмування C.

Параметри:

• Expression - Вираз, що використовується блоком для обчислення вихідного сигналу на підставі вхідного. Цей вираз складається за правилами, прийнятим для опису функцій на мові С.

У виразі можна використовувати такі компоненти:

1 Вхідний сигнал. Вхідний сигнал у вираженні позначається і, якщо він є скаляром. Якщо вхідний сигнал - вектор, необхідно вказувати номер елемента вектора в круглих дужках. Наприклад, u(1) і u(3) - перший і третій елементи вхідного вектора.

2 Константи.

3 Арифметичні оператори (+ - * /).

4 Оператори відносини (==! => <> = <=).

5 Логічні оператори (&& | |!).

6 Круглі дужки.

1. 7 Математичні функції: abs, acos, asin, atan, atan2, ceil, cos, cosh, exp, fabs, floor, hypot, ln, log, log10, pow, power, rem, sgn, sin, sinh, sqrt, tan, и tanh.

8 Змінні з робочої області. Якщо змінна робочої області є масивом, то її елементи повинні вказуватися за допомогою індексів в круглих дужках. Напрмер, A(1,1) - перший елемент матриці A.

Оператори відносини і логічні оператори повертають значення у вигляді логічного нуля (FALSE) або логічної одиниці (TRUE).

Оператори, які допускаються до використання у виразі, мають такий пріоритет (в порядку убування):

1 ()

2 + - (унарні)

3 Зведення в ступінь

4!

5 /

6 + - (бінарні)

7> << => =

8 =, =

9 &&

10 | |

Блок не підтримує матричні і векторні операції. Вихідний сигнал блоку завжди - скаляр.

Приклади використання блоку Fcn показані на рис. 17.

Рисунок 17-Приклади використання блоку Fcn