Числовые характеристики выборки: средняя выборочная, выборочная дисперсия, выборочное среднее квадратическое отклонение.
Выборочная средняя Xв(с черточкой)=Сумма(xini)/n. Является несмещенной оценкой математического ожидания, т.к. М(Xв(с черточкой))=М(х)
Выборочная дисперсия Dв=сумма((xi- Xв(с черточкой))2ni)/n. Характеризует разброс значений относительно Xв(с черточкой). Является смещенной оценкой дисперсии.
Выборочное среднеквадратическое отклонение σв=sqrt(Dв)
Точечные статистические оценки и их свойства
Статистическая оценка -- приближенное значение вероятностных характеристик законов распределения, полученных на основе статистических или выборочных данных. Точечная статистическая оценка -- статистическая оценка, выражаемая одним числом.
Оценка называется несмещённой, если её математическое ожидание равно оцениваемому параметру генеральной совокупности
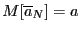
Оценка называется состоятельной, если она по вероятности с увеличением объема выборки n стремится к параметру генеральной совокупности
Оценка называется эффективной, если она обладает минимальной дисперсией среди всех возможных несмещенных точечных оценок.
Интервальные оценки. Доверительный интервал. Интервальная оценка математического ожидания нормального распределения
Интервальной называют оценку, которая определяется двумя числами—концами интервала. Интервальные оценки позволяют установить точность и надежность оценок.
Интервальные оценки применяют при небольших объемах выборки.
Доверительным называется интервал, внутри которого с определенной доверительной вероятностью (надежностью) заключен оцениваемый параметр.
Интервальная оценка среднего квадратического отклонения нормального распределения.
http://apollyon1986.narod.ru/docs/TViMS/NP/lekziitv/lekziya13.htm#1. Точечные оценки параметров распределения.
Точность и надежность интервальных оценок http://gendocs.ru/v2031/?cc=5&page=7
Точечной называют оценку, которая определяется одним числом.
Проверка гипотезы о нормальной распределении генеральной совокупности. Критерий согласия Пирсона.