Вычисление степеней
Корни и степени
Степенью
называется выражение вида 
.
Здесь
— основание степени, 
— показатель степени.
Степень с натуральным показателем
Проще всего определяется степень с натуральным (то есть целым положительным) показателем.
По определению, 
.
Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы. Возвести число в квадрат — значит умножить его само на себя.
.
Возвести число в куб — значит умножить его само на себя три раза.
.
Возвести число в натуральную степень — значит умножить его само на себя раз:
Степень с целым показателем
Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.
По определению,
.
Это
верно для 
.
Выражение 
не
определено.
Определим также, что такое степень с целым отрицательным показателем.
Конечно, все это верно для , поскольку на ноль делить нельзя.
Например,
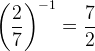
Заметим, что при возведении в минус первую степень дробь переворачивается.
Показатель
степени может быть не только целым,
но и дробным,
то есть рациональным числом. В статье
«Числовые множества» мы говорили,
что такое рациональные числа. Это числа,
которые можно записать в виде дроби 
,
где 
—
целое, 
—
натуральное.
Здесь нам понадобится новое понятие — корень -степени. Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.
Запомним правила действий со степенями:
— при
перемножении степеней показатели
складываются
— при
делении степени на степень показатели
вычитаются
— при
возведении степени в степень показатели
перемножаются
Заключение
Математика, как и любая другая наука не стоит на месте, вместе с развитием общества меняются и взгляды людей, возникают новые мысли и идеи. И XX век не стал в этом смысле исключением. Появление компьютеров внесло свои корректировки в способы решения уравнений и значительно их облегчило. Но компьютер не всегда может быть под рукой (экзамен, контрольная), поэтому знание хотя бы самых главных способов решения уравнений необходимо знать. Использование уравнений в повседневной жизни – редкость. Они нашли свое применение во многих отраслях хозяйства и практически во всех новейших технологиях.
