МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Филиал федерального государственного бюджетного образовательного учреждения

высшего профессионального образования

"Уфимский государственный нефтяной технический университет" в г. Салавате

Филиал ФГБОУ ВПО УГНТУ в г. Салавате

Кафедра "Оборудование предприятий нефтехимии и нефтепереработки"

СОГЛАСОВАНО УТВЕРЖДАЮ

Зав. кафедрой ОПНН, доцент Зам. директора по учебной работе,

______________Н.М. Захаров _______________Ф.М. Хазиев

______________ _______________

Методические указания к лабораторной работе № 6

определение коэффициента гидравлического

сопротивления при течении жидкости

в прямой круглой трубе

Дисциплина "Процессы и аппараты химической технологии.

Часть I – Гидравлика"

СОГЛАСОВАНО РАЗРАБОТАЛ

Инженер по охране труда Доцент кафедры ОПНН

_____________Г.В. Мангуткина ______________Р.Г. Худайдатов

_____________ ______________

Салават

2012

Изложена физическая сущность определения коэффициента гидравлического сопротивления в прямой круглой трубе и теории расчета. Приведены инструкции по выполнению лабораторной работы по дисциплине "Процессы и аппараты химической технологии. Часть I – Гидравлика".

Методические указания предназначены: для студентов специальности 240801 "Машины и аппараты химических производств", 240403 "Химическая технология природных энергоносителей и углеродных материалов"; для студентов-бакалавров направления 241000 «Энерго- и ресурсосберегающие процессы в химической технологии, нефтехимии и биотехнологии», профиль "Машины и аппараты химических производств"; направления 240100 «Химическая технология», профиль "Химическая технология природных энергоносителей и углеродных материалов" всех форм обучения.

© Филиал ФГБОУ ВПО Уфимского государственного нефтяного технического

университета в г. Салавате 2012.

Лабораторная работа № 6 (2 часа)

Определение коэффициента гидравлического сопротивления при течении жидкости в прямой круглой трубе

Цель работы: Экспериментальное определение коэффициента гидравлического сопротивления при течении жидкости в прямой круглой трубе; сравнение найденного значения _оп с вычисленным по формуле.

1 Общие сведения

При течении вязкой жидкости возникают силы сопротивления движению за счет внутренних сил трения между частицами и трения частиц за стенки. На преодоление сил сопротивления затрачивается часть напора жидкости.

В горизонтальной трубе равного сечения потери напора равны z₁ = z₂; ₁ = ₂; d = const

, (1)

где – показания пьезометров, установленных в начале трубы;

– показания пьезометров, установленных в конце трубы.

Для вычисления потерь напора по длине при движении жидкости по трубам пользуются формулой Дарси-Вейсбаха

, (2)

где  – коэффициент гидравлического сопротивления;

l – длина трубопровода;

d – диаметр трубы;

– скоростной напор жидкости.

Коэффициент гидравлического сопротивления теоретически определяется только для ламинарного течения жидкости. Для турбулентного режима его определяют экспериментально.

Изучая гидравлическое сопротивление в трубах с искусственной шероховатостью (искусственная шероховатость создавалась приклеиванием отсеянного песка к стенкам), И. Никурадзе получил следующую зависимость, представленную на рисунке 1.

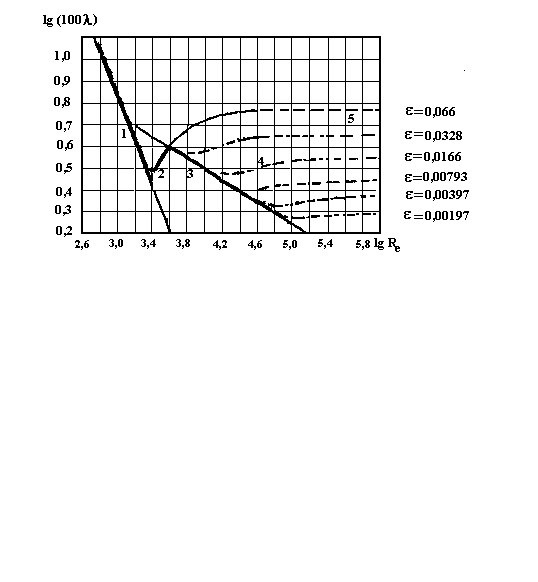
Рисунок 1 – График Никурадзе

Аналогичный вывод был получен при опытах, проведенных И.А. Исаевым, Г.А. Муриным и др. на трубах с естественной шероховатостью (промышленные трубопроводы).

Это очевидно из рисунка 2.

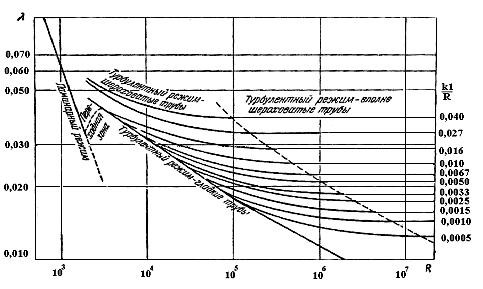
Рисунок 2 – График Мурина

В обоих случаях выявилась функциональная зависимость коэффициента гидравлического сопротивления от числа Re и относительной шероховатости поверхности трубы.

ПРИМЕЧАНИЕ: Относительной шероховатостью называется отношение трубы выступа шероховатости к радиусу трубы:

. (3)

Обратное значение – называется относительной гладкостью.

Установлено, что при турбулентном движении на стенках трубы имеется тонкий слой жидкости с ламинарным движением – ламинарная пленка, толщина которой может быть больше или меньше выступов шероховатости (рисунок 3).

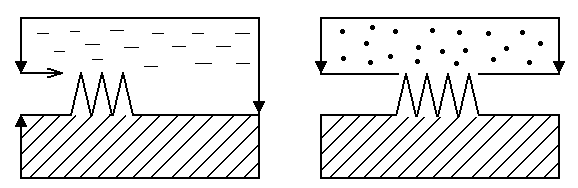
Рисунок 3 – Ламинарная пленка

Если выступы шероховатости тонут в ламинарной пленке (_пл > ), то при таком режиме трубы оказываются гидравлически гладкими. Когда при больших числах Re ламинарная пленка разрушается и на покрывает выступы шероховатости, то трубы шероховатые (_пл < ).

Вполне очевидно, из рисунков 1 и 2, что для гидравлически гладких труб коэффициент гидравлического сопротивления  = f(Re) для шероховатых  = f(Re, ). При увеличении числа Re коэффициент гидравлического сопротивления зависит только от шероховатости, что позволит при определении коэффициента гидравлического сопротивления выделить несколько зон:

1 – зона жидкого сопротивления, которая соответствует ламинарному режиму Re < Re_кp. Коэффициент определяется из формулы

. (4)

В таблице 1 приведены значения  при Re = 500  2000.

Таблица 1 – Значения  при Re = 500  2000

Re	500	1000	1500	1750	2000
	0,128	0,064	0,043	0,043	0,032

2 – переходная зона от ламинарного движения к турбулентному (Re = 2000  3500).

Френкель Р.З, предлагает определить по формуле

. (5)

Практического значения эта зона не имеет.

3 – зона гладкостенного сопротивления при слабо развитом турбулентном режиме.

Для режимов с Re  10⁵ предлагается формула Блазиуса:

. (6)

Значения по формуле Блазиуса при Re =3000  12000 приведены в таблице 2.

Таблица 2 – Значения  при Re = 3000  12000

Re	3000	4000	5000	6000	7000	8000	9000	10000	11000	12000
	0,047	0,0401	0,0376	0,0359	0,0346	0,0335	0,0325	0,0316	0,0303	0,029

для Re < 3·10⁶ – формула профессора Конакова:

. (7)

4 – зона доквадратичного сопротивления характеризуется турбулентным режимом, когда поверхность трубопровода становится шероховатой (_пл < ) и коэффициент гидравлического сопротивления зависит не только от числа Re, но и от шероховатости. Граница этой зоны иногда определяется пределами

, (8)

а коэффициент находится по разным эмпирическим формулам, например, по формуле Алышуля А.Д.

. (9)

5 – зона квадратичного сопротивления соответствует турбулентному режиму, когда изменение числа Re не оказывает влияния на коэффициент , а влияет только шероховатость.

. (10)

Для Re =  можно пользоваться формулой Никурадзе:

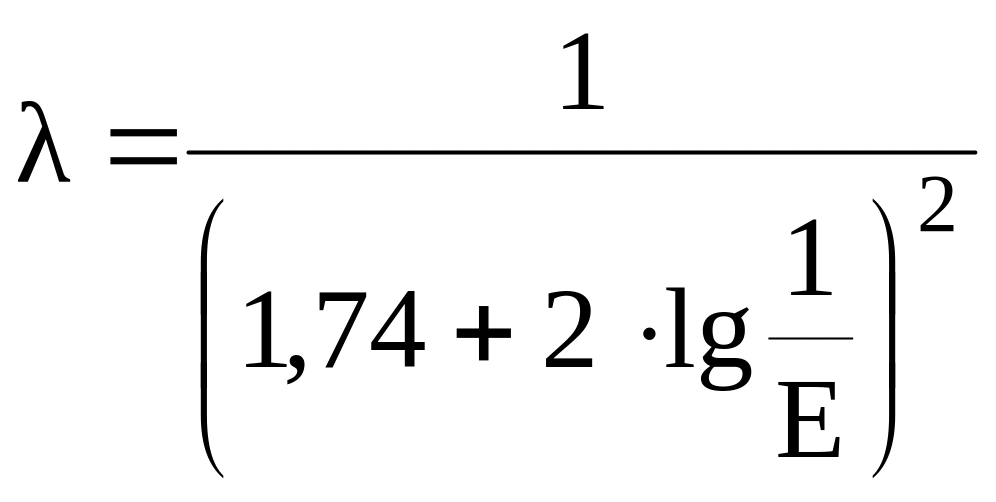, (11)

где Е – относительная шероховатость.