ПРАКТИКУМ З ДИСЦИПЛІНИ «ІНВЕСТУВАННЯ»

Задача 1

Розрахувати ціну капіталу за наступними даними, наведеними в таблиці 1.

джерела коштів	Частка %	необхідна прибутковість (цін засобів джерела) гк, %
Нерозподілений прибуток	3	15
привілейовані акції	10	12
звичайні акції	40	17
Позикові кошти:	38	18
банківські кредити облігаційну позику	9	16

Рішення

Ціна капіталу є відносною величиною і розраховується як

середньозважена величина значень необхідної прибутковості за різними джерелами фінансування, а вагами є частки кожного джерела в загальній сумі інвестицій:

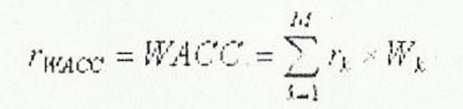
гк - необхідна прибутковість (норма прибутку) за капіталом, отриманому з Л-го джерела

]¥к - частка капіталу (інвестиційних ресурсів), одержаного з к-го джерела.

отримуємо:

Пуасс = 0,03 х 0,15 + 0,10 х 0,12 + 0,40 х 0,17 + 0,38 х 0,18 + 0,09 х 0,16 = 0,0045 + 0,012 + 0,068 + 0,0684 + 0,0144 = 0,167 = 16,7%.

Отже, ціна сукупних витрат підприємства по виплаті доходу всім власникам інвестиційних коштів складає 16,7%. Це означає, що підприємство може приймати інвестиційні рішення, очікувана рентабельність яких не нижче розрахованого показника.

Задача 2

Інвестор придбав міноритарний пакет акцій при ціні 50 крб. за акцію, через 240 днів продав весь пакет при ціні 55 крб. за акцію, отримавши за час володіння акціями дивіденди в розмірі 3-х руб. на кожну акцію. Розрахувати дохідність акції (дохідність пакета) за період володіння.

Рішення

Прибутковість акції:

г - дохідність акції з розрахунку річних

РО - ціна покупки акції

РІІ - ціна продажу акції

О - дивіденди, отримані за період володіння акцією Т - період (у днях), протягом якого інвестор володів акцією,

отримуємо:

= 0 2433 = 24 3%

Задача З

Обчислити теперішню вартість ануїтету за 5 років, якщо сума ануїтетного платежу - 700 грн., річна відсоткова ставка - 25%.

Рішення

Умови задачі дуже поверхневі: не вказаний метод нарахування ануїтетного відсотка - чи попередній (пренумерандо), чи наступний (постнумерандо). Адже від цього залежить застосовувана в розрахунках формула. Тому будемо вважати, що "наш" ануїтет здійснюється на умові попередніх платежів (пренумерандо). В цьому випадку для розрахунку теперішньої вартості ануїтету використовується формула:

В цій формулі множник (І-И)"¹ називається дисконтним множником.

В нашому випадку маємо такі вихідні дані: Б Щ 700 грн., І = 0,25, Т = 5 років. Отже, отримаємо:

РА = 700 ♦ (1 + 0,25) * (1 4- 0,25)^Л -5 / 0,25 = 1146,88 грн.

Задача 4

Обчислити майбутню вартість ануїтету через 6 років, якщо сума ануїтетного платежу — 100 гри.., річна відсоткова ставка — 24%, темп інфляції - - 5%.

Рішення

Розв'язок цієї задачі здійснюється з використанням в якості річної відстоткової ставки і = 24% реальної відсоткової ставки 1_р з урахуванням темпу інфляції = 5%:

= (0,24-0,05)7(1-і-0,05) = 0,181 = 18,1%.

З урахуванням саме цієї процентної ставки й підрахуємо майбутню вартість ануїтету, який здійснюється на умовах наступних платежів (постнумерандо):

SA = R*[(l+ t_p)^T- 1] / t_p,

де в нашому випадку R= 100 грн., t_p = 0,181, Т = 6 років. Отже:

SА = 100*[(1 +0,181 )^Л6 - 1 ]/0,181= 946,58 грн.

Задача 5

Що Ви обираєте: отримати 12000 грн. готівкою чи виплати по 2900 грн. на протязі 5 років при річній відсотковій ставці 18% з періодичністю виплат З рази на рік? (Обчислити для останнього варіанта ефективну відсоткову ставку.)

Рішення

Щоб відповісти на це запитання, треба розрахувати загальну майбутню суму Р виплат по п = 3 рази на рік за Т = 5 років з урахуванням річних відсотків t = 0,18, якщо виплати проводяться кожний рік по S = 2900 грн. Для цього застосовується формула для розрахунку простих відсотків:

Р = S*(l+t/n)*T = 2900*(l+0,18/3)*5 = 15370,05 грн.

Отже, одразу видно, що отримувати по 2900/3 = 966,67 грн. кожні 12/3 = 4 місяці навіть під такі незначні 18/3 = 6 відсотків значно вигідніше, оскільки в підсумку 12000 грн. < 15370 грн. При цьому ефективна відсоткова ставка становитиме:

t_e(|, = (P-S*T)/(S*T²) = (15370,05-2900*5) / (2900*5^Л2) = 0,012.

Такий низький відсоток - 1,2% - означає, що якби виплати проводилися 5 років по 2900 грн. без виплати будь-яких відсотків, то отримана сума 2900 * 5 = 14500 грн. виявилася б ненабагато меншою, ніж та, що ми отримали вище: уявна сума простого процента в процесі 5-річного компаундінга (нарощення вартості) склала б лише 15370,05 - 14500 = 870,05 грн. Доречі, ефективну ставку Іеф можна було б розрахувати і виходячи з отриманої суми компаундінга:

І_еф = 870,05/14500/5 = 0,012 = 1,2%.

Задача б

Торгові фірма має намір придбати товар за 400 тисяч гривень, транспортувати його до місця реалізації (вартість транспортування 32 тисячі гривень) де на протязі 2 місяців має намір реалізувати його за 580 тисяч гривень. Розрахуйте чистий дохід, ефективність та дохідність інвестиційного проекту.

Рішення

Чистий дохід = 580-400-32 = 148 тис. грн.

Ефективність: 580 / 432 = 1,34 або (580-432) / 432 = 0,34

Дохідність: [(580 - 432)* 12] / (432*2) = 2,06.

Підприємство має намір придбати технологічну лінію по виробництву валів. При якому мінімальному обороті це придбання окупиться якщо змінні витрати у перерахунку на один вал становлять 80 гривень, постійні витрати (оренда, комунальні платежі, заробітна плата та ін.) - 5000000 гривень на місяць. Вартість одного валу 120 гривень. Визначити точку безбитковості.

Рішення

Точка беззбитковості ВЕР = 5000000 / (120-80) = 125000.

Задача 8

Річний обсяг закупівлі товару комерційною фірмою становить Су=100 тисяч гривень, річний обсяг продажу — Б = 135 тис. грн. Щорічні витрати на оренду приміщення, упаковку, оплату праці персоналу складають Сс=28 тисяч гривень. Який мінімальний річний обсяг продажу при якому фірма немає збитків (мінімальний річний оборот)?

Рішення

З системи формул ВЕР = Сс / (1 - Ст) та Сш = Су / Б випливає наступна формула: ВЕР = Сс /[1 - (Су / 8)] = 28000 / (1 - 100000:135000) = 28000 / 0,26 = 107692,31 (округлено 107693).

Задача 9

Підприємство має на рахунку у банку 1,2 мільйони гривень. Банк нараховує 12,5% річних. Існує пропозиція ввійти усім капіталом до спільного підприємства, при цьому прогнозується подвоєння капіталу через 5 років. Чи варто приймати таку пропозицію?

Рішення

Розрахуємо дохідність даної пропозиції. З формули FV=РV(1+і)^п маємо: 2400000 = 1200000 (1+і)⁵; 2=(1+і)⁵;

і=2^|/5 - 1; і=15%, що більше, ніж у пропозиції вкладання всієї суми в банк. Проте даний варіант вкладання коштів (входження до спільного підприємства) є більш ризиковим, ніж вкладання в банк. Отож, таку пропозицію варто приймати за умови, якщо ліквідність активу дорівнює ступеню ризику.

Задача 10

У вашому розпорядженні 10 мільйонів гривень і хотіли б подвоїти цю суму через 5 років. Яким є мінімально прийнятне значення процентної ставки?

Рішення

За формулою FV=РV(1+і)^п (формула складних процентів): 20000000 = 10000000 (1+і) процентна ставка дорівнює 15%. За формулою РУ=РУ(1+іп) [формула простих процентів]: 20000000 = 10000000 (1+5І) і в цьому випадку процентна ставка становитиме 20%.

Задача 11

Фірмі необхідно накопичити 2 мільйони гривень для придбання через 10 років будівлі під офіс. Найбільш безпечним способом накопичення є придбання безризикових державних цінних паперів, що генерують річний дохід по ставці 8% річних при нарахуванні відсотків кожні півроку. Яким повинен бути початковий внесок фірми.

Рішення

За формулою FV=РV(1+і)" (формула складних процентів) нам невідоме значення РУ: 2000000 = РУ(1+0,08)¹⁰; 2000000 = РУ*2,16 ця сума становитиме 925925,9 гри. За формулою РУ=РУ(1+іп) [формула простих процентів] нам також невідоме значення РV: 2000000 = РV (1+10 * 0,08) значення РУ становитиме 1111111,1 грн.

Задача 12

Розрахуйте теперішню вартість 1000 гривень які будуть отримані через 12 років маючи на увазі що ставка дисконтування (вартість капіталу, процентна ставка, дисконтна ставка, ставка капіталізації) становить 12 відсотків.

Рішення

За формулою FV=РV(1+і)^п маємо: 1000 = РV (1+0,12)¹²; 1000 = РV * 3,896; РV = 256,7 грн.

Задача 13

Розрахуйте теперішню вартість 623 гривень, що будуть отримані через 8 років плюс 1092 гривень, які будуть отримані через 8 років після цього, за умови, що процентна ставка становить 7 відсотків.

Рішення

За формулою FV=РV(1+і)^п маємо: РV=[623 / (1+0.07)⁸]+[Ю92 / (1+0.07)¹⁶] = (623 / 1,72)+(1092/2,95) =732,4 грн.

Розрахуйте теперішню вартість 10-ти річного ануїтету вартістю 100 гривень, за ставкою 20% річних.

Рішення

За формулою РУа = X * [(1/і) + [1 / (і*(1+і)^п)]] маємо: РУа = 100 * [(1 / 0.2) + [1 / (0.2*(1+0.2)¹⁰)] = 419 гри.

Задача 15

Розрахуйте теперішню вартість 250 гривень отримуваних щорічно на протязі 21 року плюс 1200 гривень що будуть отримуватися довічно після 22 року за умови, що річна процентна ставка становитиме 11 відсотків.

Рішення

За формулою обчислення ануїтету РУа = X * [(1/і) + [1 / (і*(1+і)^п)]] розрахуємо теперішню вартість 250 гривень: РУа = 250 * [(1 / 0.11) + [1 / (0.11*(1+0.11)²¹)] = 250*(9.09+1.0І) = 2525 грн. За формулою обчислення ануїтету с] розрахуємо теперішню вартість 1200 гривень: РУа = 1200*[1 / (0.11*( 1+0.11)²²)] = 1092. Сукупна РУа становить 1092+2525=3617 грн.

Задача 16

Фірма має намір придбати обладнання вартістю 20000 гривень. Розраховано, що річна економія від встановлення цього обладнання становитиме 5000 гривень, тривалість експлуатації становитиме 5 років а залишкова вартість 1000 гривень. Маючи на увазі, що показник норми дохідності, що вимагається становить 10%, які дії ви б порекомендували?