Исходные данные:

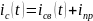
Определим начальные условия

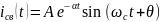
Zвх= p=jw

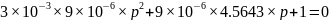
P1,2=-

=6038

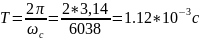
Эквивалентная схема имеет вид:

iпр=0

UL(0)=i*2R=(E/2R)*2R=E=80

,при t=0

A=8.92

Ic(t)=8.92*

	0	0,00013	0,001	0,0038	0,0045	0,00485	0,00506
	8,919997	5,722387	4,052579	-0,28973	-0,13224	-0,12004	0,124765

(брал маленький шаг)

Задание №3 р асчет формы и спектра сигналов при нелинейных преобразованиях

К нелинейному элементу (полупроводниковому диоду) приложено напряжение, имеющее постоянную и переменную составляющие

u(t) = U₀ +U_m ∙ cos ωt

В расчетном задании используется кусочно-линейная аппроксимация ВАХ нелинейного элемента. При u(t)<U₁ (U₁ – пороговое напряжение) диод смещен в обратном направлении и не пропускает ток, его сопротивление R_д стремится к бесконечности. При u(t)≥U₁ диод смещен в прямом направлении и его ток линейно зависит от приложенного напряжения. Наклон ВАХ нелинейного элемента характеризуется крутизной S = ∆I/∆U [мА/B]. Величина, обратная крутизне, является сопротивлением диода в прямом направлении R_д = 1/S.

Исходные данные

• номер группы №_гр=026 (abc), номер студента по журналу №_ст=12 (km);

• постоянная составляющая входного сигнала U₀ = 0,5 [B], пороговое напряжение нелинейного элемента U₁ = 1 [B];

• амплитуда переменной составляющей входного напряжения

U_m = 1 +0,1c = 1,6 [B];

• крутизна ВАХ нелинейного элемента S = c + №_ст = 20 [мА/В];

• период колебаний переменной составляющей входного напряжения

T = №_ст = 14 [мкс], частота ω = 0,45∙10⁶

Требуется:

1. рассчитать угол отсечки ϴ, в радианах и градусах

cosϴ = (U₁ – U₀)/U_m = (1-0,5)/1,6 = 0,3125

ϴ = arcos 0,31 = 71,94° = 1,26 рад.;

2. рассчитать амплитуду тока диода

I_m = S∙U_m∙(1-cosϴ) = 20∙10^-3∙1,6∙0,69 = 22,08 [мА];

3. записать выражение для мгновенного значения тока

i(t) = (I_m/(1-cosϴ))∙(cos ωt - cosϴ) = (22,08∙10^-3/0,69)∙(cos( 3,14∙10⁶ )– 0,31) = 0,032∙cos (0,45∙10⁶ t)– 0,00992;

4. вычислить постоянную составляющую тока

I₀ = I_m∙((sinϴ - cosϴ)/π(1 – cosϴ)) = 22,08∙10^-3∙((0,95-1,26∙0,31)/(3,14∙0,69)) = 5,7 [мА];

5. изобразить временные диаграммы напряжения u(t)и тока i(t):

6. вычислить амплитуду первой гармоники тока

I_m1 = I_m∙((ϴ - sinϴ∙cosϴ)/π∙(1-cosϴ)) = 22,08∙10^-3∙((1,26-0,95∙0,31)/(3,14∙0,69)) = 9,86 [мА];

7. используя общее выражение для n – ой гармоники тока

I_mn = I_m∙((2(sinϴ∙cosϴ - n∙cos(n∙ϴ)∙sinϴ)/(π∙n∙(n² – 1)∙(1-cosϴ)))

I_m2 = 22,08∙10^-3∙(((2(0,95∙0,31 - 2∙(-0,81)∙0,95))/12,9996 )= 6,172 [мА];

I_m3 = 22,08∙10^-3∙(((2(0,29 - 3∙(-0,8)∙0,95))/51,998) = 2,18 [мА];

I_m4 = 22,08∙10^-3∙(((2(0,29 - 4∙0,32∙0,95))/129,996) = -0,3 [мА];

I_m5 = 22,08∙10^-3∙(((2(0,29 - 5∙0,9999∙0,95))/259,992) = -0,75 [мА];

8. По полученным данным построить диаграмму спектра тока нелинейного элемента

9. Используя вычислительные возможности программы MathCAD, построить временную диаграмму тока для первых пяти гармоник

i(t) = I₀ + I_m1∙cos ω₁t + I_m2∙cos 2ω₁t + I_m3∙cos 3ω₁t + I_m4∙cos 4ω₁t + I_m5∙cos 5 ω₁t

i(t) = 5,7 + 9,86∙cos 0,45∙10⁶ t+6,172 ∙cos 2∙0,45∙10⁶ t+ 2,18∙cos 3∙0,45∙10⁶ t-0,3∙cos 4∙0,45∙10⁶t– 0,75∙cos 5∙0,45∙10⁶

Временные диаграммы для кождой гармоники: