1.3 Розрахунок і побудова природних і штучних характеристик електроприводу

В; об/хв.; об/хв.;

Механічна характеристика асинхронного двигуна являє собою залежність швидкості від електромагнітного моменту. Для побудови механічної характеристики АД з фазним ротором використаємо рівняння Клосса в спрощеному вигляді:

(3.1)

де Мк - критичний момент, який розвиває двигун, Нм;

Sк - критичне ковзання. яке відповідає величині Мк;

S – ковзання.

Дане рівняння дозволяє по паспортних даних вибраного АД побудувати природну характеристику. Маючи визначене в 2 розділі значення номінального моменту.

визначаємо критичний момент по формулі:

;

Номінальне значення ковзання визначаю за формулою:

(3.3)

де = 1000 об/хв - синхронна частота обертання даного АД;

Критичне значення ковзання визначаю по формулі:

(3.4)

Виходячи з формули 3.3:

об/хв.

Задаючись кількома значеннями ковзання на проміжку від 1 до 0 по рівнянню 3.1 будуємо природну механічну характеристику ДПС.

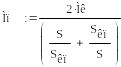
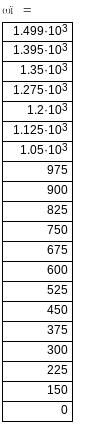
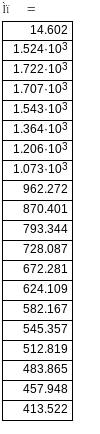
Проводжу побудову штучних характеристик АД. Реостатні характеристики будуємо на основі заданих значень додаткових опорів в колі ротора. Для побудови реостатних характеристик визначаємо активний опір обмотки ротора по формулі:

_(3.5)

де - номінальна лінійна напруга при нерухомому роторі;

- номінальний струм ротора.

В; А.

Ом.

При введенні в реостатне коло додаткового опору буде змінюватись критичне ковзання двигуна, оскільки воно пропорційне . Для визначення критичного ковзання для природної і штучної характеристики служить формула:

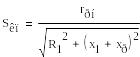_(3.6)

,

де - активний опір статора;

- реактивний опір статора;

- реактивний опір ротора.

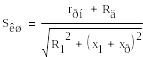_(3.7)

де - додатковий активний опір в обмотці ротора.

Поділивши перше рівняння на друге, одержую:

_(3.8)

Звідки

_(3.9)

Отже

Підставляючи по черзі одержані значення критичних ковзань в формулу 3.1, розраховую дані для побудови штучних характеристик:

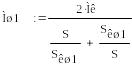
при

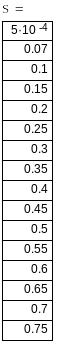
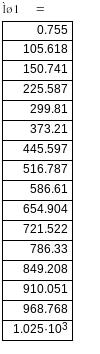
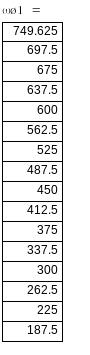
При

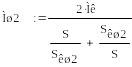
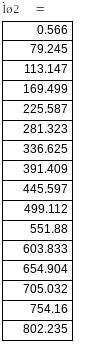
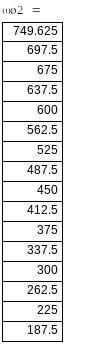
При зміні напруги на вході АД критичний момент буде змінюватись в квадратичній залежності, оскільки він пропорційний квадрату вхідної напруги:

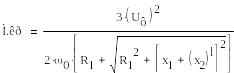_(3.10)

де - індуктивний опір ротора, приведений до обмотки статора.

Тому

Одержане значення критичного моменту підставляємо в формулу 3.1, розраховуємо декілька значень для побудови механічної характеристики при пониженій напрузі.

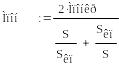
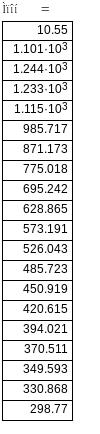
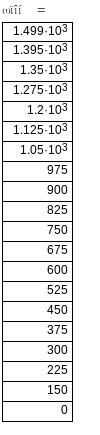
Рисунок 1.2 – Природні і штучні механічні характеристики АД з фазним ротором.