
- •Область определения
- •График функции двух переменных
- •Предел функции 2-х переменных в точке.
- •3.1. Определение частных производных
- •3.3. Геометрический смысл частных производных функциии 2-х переменных
- •Достаточное условие дифференцируемости фнп
- •Касательная плоскость и нормаль к поверхности
- •Полный дифференциал (определение, форма, геометрический смысл).
- •Частные производные высших порядков. Теорема о равенстве смешанных частных производных.
Полный дифференциал (определение, форма, геометрический смысл).
Полный дифференциал
функции f (x, у, z,...) нескольких независимых переменных — выражение
![]()
в случае, когда оно отличается от полного приращения
Δf = f (x + Δx, y + Δy, z + Δz,…) - f (x, y, z, …)
на величину, бесконечно малую по сравнению с
![]()
Частные производные высших порядков. Теорема о равенстве смешанных частных производных.
Пусть
задана функция f(x,
y).
Тогда каждая из ее частных
производных(если
они, конечно, существуют) ![]() и
и ![]() ,
которые называются также частными
производными первого порядка,
снова являются функцией независимых
переменных x,
y и
может, следовательно также иметь частные
производные. Частная производная
,
которые называются также частными
производными первого порядка,
снова являются функцией независимых
переменных x,
y и
может, следовательно также иметь частные
производные. Частная производная  обозначается
через
обозначается
через ![]() или
или ![]() ,
а
,
а 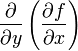 через
через ![]() или
или ![]() .
Таким образом,
.
Таким образом,
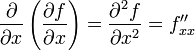 ,
, 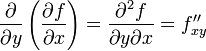
и, аналогично,
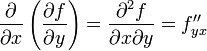 ,
, 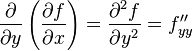 .
.
Производные ![]() и
и ![]() называются частными
производными второго порядка. Определение:Частной
производной второго порядка от функции
z=f(x;y) дифференцируемой в области
D,называется первая производная от
соответствующей частной производной.
Рассматривая частные производные от
них, получим всевозможные частные
производные третьего порядка:
называются частными
производными второго порядка. Определение:Частной
производной второго порядка от функции
z=f(x;y) дифференцируемой в области
D,называется первая производная от
соответствующей частной производной.
Рассматривая частные производные от
них, получим всевозможные частные
производные третьего порядка: ![]() ,
, ![]() ,
, ![]() и т. д.
и т. д.
Определение точки максимума и минимума функции Z=f(x,y).
Необходимый признак экстремума функции Z=f(x,y). Достаточный признак экстремума.
§5. Экстремум функции двух переменных |
Пусть
функция Функция Аналогично определяется минимум функции. Максимум и минимум функции называются экстремумами функции. Теорема (необходимое
условие экстремума). Если
–точка
экстремума функции
, то
частные производные Точки,
в которых частные производные Сформулированный признак не является достаточным: не обязательно критическая точка является точкой экстремума. Чтобы проверить, есть ли экстремум в критической точке, используют следующую теорему (достаточное условие экстремума). Пусть
в некоторой области, содержащей
точку
, функция
имеет
непрерывные частные производные до
3–го порядка включительно
и 1)если 2)если 3)если |
Определение производной функции U=U(x,y,z) по заданному направлению в данной точке. Формула для вычисления.
Производная по направлению.
Рассмотрим функцию u(x, y, z) в точке М( x, y, z) и точке М1( x + x, y + y, z + z).
Проведем
через точки М и М1 вектор ![]() . Углы
наклона этого вектора к направлению
координатных осей х, у, z обозначим
соответственно , , .
Косинусы этих углов называются
направляющими косинусами вектора
.
. Углы
наклона этого вектора к направлению
координатных осей х, у, z обозначим
соответственно , , .
Косинусы этих углов называются
направляющими косинусами вектора
.
Расстояние
между точками М и М1 на
векторе
обозначим S. Абсолютный
экстремум ФНП Допустимая
точка ![]() называется
точкой абсолютного минимума (или
максимума) ФНП
называется
точкой абсолютного минимума (или
максимума) ФНП ![]() ,
, ![]() в
задаче (*), если
выполняется
условие:
в
задаче (*), если
выполняется
условие: ![]()
![]() или
или
![]() .
.
![]()
Высказанные выше предположения, проиллюстрируем на рисунке:

Далее предположим, что функция u(x, y, z) непрерывна и имеет непрерывные частные производные по переменным х, у и z. Тогда правомерно записать следующее выражение:
![]() ,
,
где
величины 1, 2, 3
– бесконечно малые при ![]() .
.
Из геометрических соображений очевидно:
![]()
Таким образом, приведенные выше равенства могут быть представлены следующим образом:
![]() ;
;
![]()
Заметим, что величина s является скалярной. Она лишь определяет направление вектора .
Из этого уравнения следует следующее определение:
Определение:
Предел ![]() называется
производной функции u(x, y, z) по направлению
вектора
в
точке с координатами ( x, y, z).
называется
производной функции u(x, y, z) по направлению
вектора
в
точке с координатами ( x, y, z).
Градиент функции U=U(x,y,z). Связь градиента с производной по направлению, свойства градиента.
Градиентом функции многих переменных в данной точке называется вектор, координаты которого равны частным производным по соответствующим аргументам, вычисленным в данной точке.
![]() .
.
Теорема: Пусть задана функция u = u(x, y, z) и поле градиентов
![]() .
.
Тогда
производная ![]() по
направлению некоторого вектора
равняется
проекции вектора gradu на
вектор
.
по
направлению некоторого вектора
равняется
проекции вектора gradu на
вектор
.
1. Производная
в данной точке по направлению
вектора ![]() имеет
наибольшее значение, если направление
вектора
совпадает
с направлением градиента. Это наибольшее
значение производной равно
имеет
наибольшее значение, если направление
вектора
совпадает
с направлением градиента. Это наибольшее
значение производной равно ![]() .
.
2. Производная
по направлению вектора, перпендикулярного
к вектору ![]() ,
равна нулю.
,
равна нулю.
