1. Определение функции 2-х переменных, область определения, график.

Функция Z называется функцией нескольких переменных x, y, если:

1.      Задано множество Д пар численных значений: Д=(x,y ϵ R)

2.      Задан закон, по которому каждой паре чисел из этого множества ставится соответствующее численное значение Z=f(x, y)

Если каждой совокупности значений переменной (х1, х2 …. хn) из некоторой области V соответствует определенное значение переменной W, то W называется функцией нескольких переменных.

Область определения

Область определения функции нескольких переменных – некоторая область в плоскости XOY.

График функции двух переменных

Графиком функции двух переменных в декартовой прямоугольной системе координат в пространстве является поверхность, проектирующаяся на плоскость XOY в область определения функции.

2. Предел функции 2-х переменных в точке.

Предел функции двух переменных 

Число b называется пределом функции z=f(x,y)=f(P0) при Р→Р0, если для любого сколь угодно малого ε>0 существует δ окружность точки Р0(х0, y0):

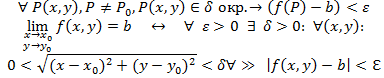
По определению предела, предел функции двух переменных не зависит от направления движения точки P к точке P₀, поэтому, если окажется, что при P →P₀ с разных сторон f(P) стремится к разным предельным значениям, то функция f(P) предела не имеет. Функция z=f(x,y)  непрерывна в точке Р0, если бесконечно малому расстоянию ρ=РР₀, соответствует бесконечно малое приращение функции Δz.

3. Частные приращения функции Z=f(x,y), частные производные (опр и геом смысл).

3.1. Определение частных производных

Рассмотрим функцию  , непрерывную в точке   и некоторой её окрестности.

 – это частное приращение функции z(x,y) по аргументу x;

– это частное приращение функции z(x,y)  по аргументу у;

 – это частная производная функции z(x,y)  по аргументу x;

 – это частная производная функции (x,y) z по аргументу у.

ОПРЕДЕЛЕНИЕ ЧАСТНОЙ ПРОИЗВОДНОЙ ФНП

Частной производной функции нескольких переменных по одному из её аргументов называется конечный предел отношения частного приращения функции по этому аргументу к приращению аргумента при условии, что приращение аргумента стремится к нулю

3.3. Геометрический смысл частных производных функциии 2-х переменных

 –  это есть угловой коэффициент касательной к сечению поверхности   плоскостью y=y₀, рис. 10.

 – это есть угловой коэффициент касательной к сечению поверхности   плоскостью х=х₀, рис.11. 

4. Полное приращение функции Z=f(x,y). Два определения функции, непрерывной в точке.

Полным приращением функции двух переменных   в точке   называется выражение  .

Предположим, что в точке   и некоторой ее окрестности функция z = f(x,y) имеет непрерывные частные производные первого порядка   и  . Выразим через них полное приращение  :

 (1) где  заключено между   и  ,   заключено между   и  , рис. 11.

Так как по предположению частные производные непрерывны, то:

        

(по связи функции, её предела и бесконечно малой),  где ₁  и ₂ – бесконечно малые при х0 и у0, то есть при  .

Таким образом, полное приращение   функции   выразилось следующим образом:

 (2)

Каждое из слагаемых ΙΙ является б.м. более высокого порядка малости относительно  . Действительно,

    при  .

Аналогично      +  при  .

Ι слагаемое – линейное относительно x и y, оно является главной частью полного приращения z.

 

ОПРЕДЕЛЕНИЯ ДИФФЕРЕНЦИРУЕМОЙ ФНП, ПОЛНОГО ДИФФЕРЕНЦИАЛА ФНП

Функция z = f(x,y), полное приращение z которой в данной точке (x;y) может быть представлено в виде суммы двух слагаемых: выражения, линейного относительно x и y, и величины, бесконечно малой более высокого порядка малости, чем  , называется дифференцируемой ФНП в данной точке; главная часть ее полного приращения, линейная по приращениям аргументов, называется полным дифференциалом ФНП:                                                       (3)-

5. Определение дифференцируемой функции Z=f(x,y) в точке и ее свойства (с док-вом). Достаточное условие дифференцируемости.

ОТВЕТ ВЫШЕ (половина)