Другие характеристики вариационного ряда

Модой называют вариацию, которая имеет наибольшую частоту.

Пример:

xi	4	7	9
ni	1	20	6

.

Медианой называют варианту, которая делит вариационный ряд на две равные части по числу вариант.

Если число вариант , то , если , то .

Пример:

xi	2	3	5	6	7
ni	12	18	30	12	6

.

xi	2	3	5	6	7	9
ni	12	18	30	12	6	14

Размахом варьирования R называют

Для предыдущего примера .

Средним абсолютным отклонением называют

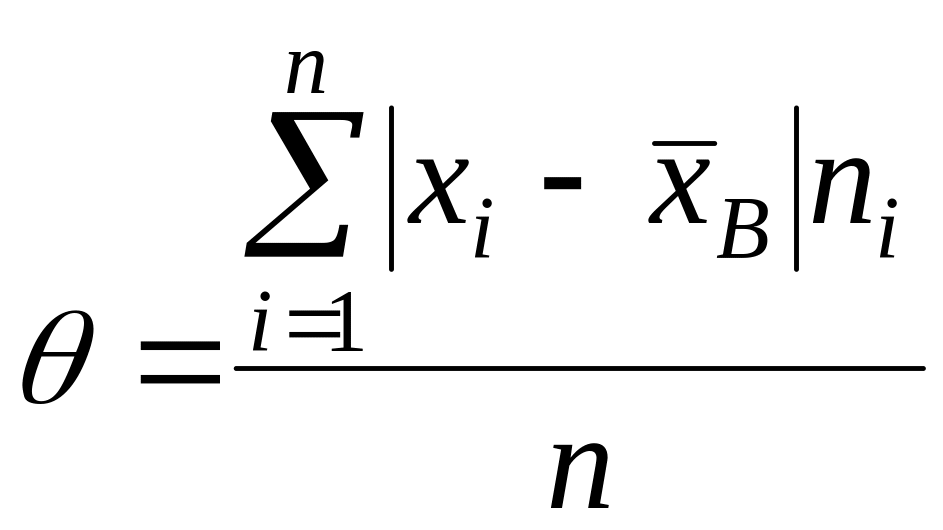
Пример:

xi	1	3	6	16
ni	4	10	5	1

,

.

служит для характеристики рассеяния ряда.

Коэффициент вариаций V

.

служит для сравнения величин рассеяния двух вариационных рядов. Тот ряд имеет больше рассеяние, у которого больше.

Статистические оценки

Определение: Точечной оценкой называют оценку, которая определяется одним числом. Все оценки, рассмотренные выше, являются точечными.

При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. Поэтому, при небольшом объеме выборки следует пользоваться интервальными оценками.

Определение: Интервальной называют оценку, которая определяется двумя числами – концами интервала. Интервальные оценки позволяют установить точность и надежность оценок.

Пусть - параметр, - найденная по данным выборки статистическая характеристика. Она служит оценкой неизвестного параметра . Ясно, что чем меньше , тем точнее определяется параметр . Другими словами, если и , то чем меньше , тем точнее .

Определение: Вероятность называется надежностью (доверительной вероятностью). Обычно надежность оценки задается заранее, причем в качестве берут число, близкое 1. Наиболее часто задаются надежности 0,95;0,99 и 0,999.

По другому можно записать .

Это соотношение следует понимать так: вероятность того, что интервал заключает в себе (покрывает) неизвестный параметр , равна .

Интервал называется доверительный интервал.

Возможные задачи:

I . Если X распределено нормально, значит параметров 2. Пусть среднее квадратичное отклонение известно. Оценить неизвестное математическое ожидание по выборочной средней.

Найдем , т.е. .

Решение основано на формуле

Заменим в этой формуле через . В результате несложных преобразований, получается

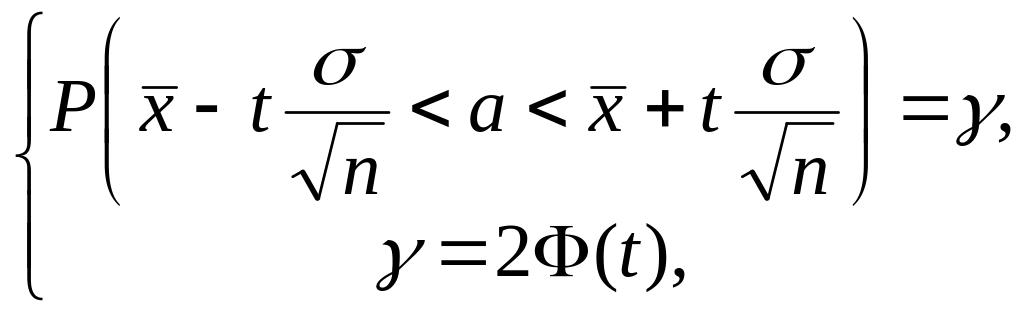
где .

Число определяется из по таблице функции Лапласа.

Замечание: 1) при возрастании объема выборки n число убывает, следовательно, точность оценки увеличивается.

2)при увеличении надежности оценки, т.е. , t – возрастает, т.к. возрастающая функция, а значит - возрастает. Следовательно, увеличение надежности влечет за собой уменьшение ее точности.

Пример: Случайная величина X имеет нормальное распределение с известным =3. Найти доверительные интервалы для оценки неизвестного математического ожидания по выборочным средним, если объем выборки n=36 и надежность оценки .

Решение: , значит, .

.

Доверительный интервал .

II . Пусть X распределено нормально и среднее квадратичное отклонение неизвестно. Оценить неизвестное математическое ожидание при помощи доверительных интервалов.

,

где s – исправленное среднее квадратичное значение, а = ищется по приложению 3 по и n.

Пример: Количественный признак X генеральной совокупности имеет нормальное распределение. По выборке объема n=16 найдены и s=0,8. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью .

Решение: , значит, .

.

Доверительный интервал .

III . Пусть X распределено нормально. Требуется оценить по исправленному выборочному среднему отклонению s, т.е.

,

где - ищется по приложению 4.