Механічні коливання та хвилі

1. Коливальний рух

Рух, при якому тіло послідовно зміщується то в один, то в інший бік від положення рівноваги, називається коливним або механічним коливанням. (Гілки дерев, маятник у годиннику, поршні в двигунах внутрішнього згоряння, струни музикальних інструментів). Ці рухи повторюються через однакові проміжки часу, тому називаються періодичними. Вони широко поширені в природі і використовуються людиною.

2.Умови виникнення коливань

Існують такі умови виникнення вільних коливань: 1) при виведенні тіла з положення рівноваги повинна виникати сила, яка б повертала його до положення рівноваги; 2) тертя в системі повинно бути найменшим.

3. Вільні коливання

Група тіл, в якій можуть виникати коливання, називається коливною системою. Сили, з якими тіла коливної системи взаємодіють між собою, називаються внутрішніми, а всі інші - зовнішніми.

Коливання, які відбуваються під дією внутрішніх сил, коли система виведена з положення рівноваги, називаються вільними.

4. Гармонічні коливання

Підвісимо на нитці лійку з вузьким вихідним отвором, насиплемо в неї пісок і змусимо її коливатися. Одночасно будемо переміщувати під лійкою папір перпендикулярно до її коливань. Пісок буде висипатися на папір і утворюватиме лінію синусоїду або косинусоїду в залежності від того, з якої точки починалось коливання лійки. Це говорить про те, що координата тіла, яке здійснює вільні коливання, змінюється в часі за законом sin або cos. Періодичні зміни фізичної величини за законом sin або cos називають­ся гармонічними коливаннями.

Під час коливань гармонічно змінюється швидкість, прискорення та рівнодійна всіх сил, що діють на коливальне тіло.

5. Додавання гармонічних коливань

Гармонічні коливання фізичної величини зображуються синусоїдою, якщо коливання починаються з положення рівноваги.

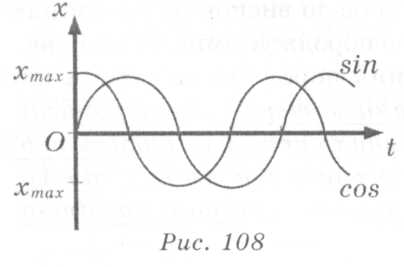
Косинусоїдою гармонічні коливання зобра­жуються тоді, коли вони починаються з мак­симального значення (відхилення) фізичної величини.

Для порівняння гар­монічних коливань їх записуюють через однакову фун­кцію (cos або sin), cos φ = sin (φ + π/2).

Графічне зображення коливального руху у вигляді вектору на площині, який обертається проти годин­никової стрілки з циклічною частотою w, називаєть­ся векторною діаграмою.

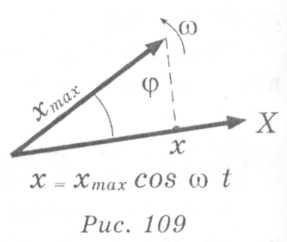
За допомогою векторних діаграм зручно додавати гармонічні коливання.

Результуюче зміщення дорівнює геометричній сумі зміщень окремих коливань у даний момент часу (прин­цип суперпозиції). Модуль амплітуди результуючого коливання знаходиться за теоремою косинусів, а початкова фаза – через тангенс початкової фази результуючих коливань.

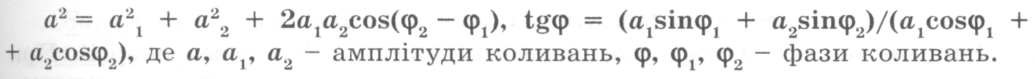
6. Амплітуда, період і частота коливань

Мінімальний проміжок часу, через який рух повторюється, називається періодом, позначається Т, вимірюється в секундах,

Кількість коливань, здійснених за одиницю часу, називають частотою коливань,

Циклічна частота – це кількість коливань, що здійснюється за 2π секунд,

Відстань від коливального тіла до положення його рівноваги називається зміщенням, х (м). Під час коливального руху зміщення постійно змінюєть­ся з часом.

Модуль максимального зміщення називається амплітудою коливань,

7. Рівняння гармонічних коливань

■О

Геометричною моделлю коливаль­ного руху є проекція обертального руху тіла по колу.

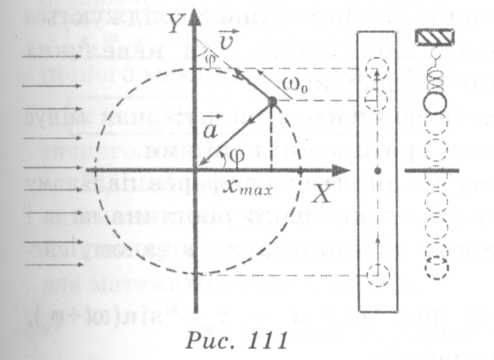
Підберемо такий обертальний рух, щоб період обертання співпадав з періодом коливання, а проекція руху кульки по колу співпадала з рухом кульки на пружині під дією сили пружності яка надає кульці прискорення. Положення проекції кульки на горизонтальну вісь знахо­диться Якщо вісь взяти вертикально, то В обох випадках координата тіла, яке здійснює вільні ко­ливання, змінюється за законом sin або cos. Періодичні зміни фізичної вели­чини за законом sin або cos називаються гармонічними коливаннями.

Залежність координати (зміщення) тіла від часу називається рівнян­ням коливального руху або рівнянням гармонічних коливань.

З обертального руху можна знайти проекцію швидкості обертання на вісь х-ів:

Аналогічно знайдемо проекцію прискорення руху тіла по колу на вісь х-ів:

8. Фаза коливань

Величина, яка стоїть під знаком cos чи sin, визначає стан коливної системи в будь-який момент часу, називається фазою,

Фаза повторюється через 2π радіан, а в часі це повторення відбувається через період (Т), тобто

9. Затухання вільних коливань

Реальні механічні коливання не відбуваються без втрат енергії. При будь-якому механічному русі тіл у наслідок їхньої взаємодії з оточуючими тілами частина механічної енергії перетворюється у внутрішню енергію теплового руху атомів і молекул. Амплітуда коливань поступово зменшується, і через деякий час після початку коливань маятник зупиняється.

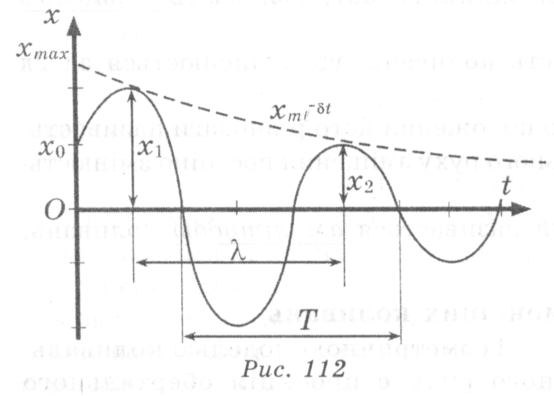
Вільні коливання тягарця на пружині чи маятника є гармонічни­ми лише тоді, коли немає тертя. Спостереження за вільними коли­ваннями маятників показують, що їхня амплітуда поступово змен­шується і через деякий час коливан­ня припиняються. Амплітуда затухаючих коливань і період залежать від характеру сил опору. Найпростіше досліджуються малі коливання для невеликих швидкостей під дією сили опору пропорційної швидкості.

– стала, яку називають коефіцієнтом опору; знак мінус показує , що сила опору і швидкість мають протилежні напрями.

Рівняння коливального руху при цьому запишеться в диференціальному вигляді Поділивши всі члени цього рівняння на т і позначивши одержимо рівняння руху в такому вигляді:

Розв'язком цього рівняння є така функція

, е - основа натуральних логарифмів.

З рівняння залежності зміщення від часу видно, що внаслідок спільної дії пружних сил і сил опору система здійснює коливальний рух, амплітуда якого зменшується з часом за експоненціальним законом, тобто в системі виникають затухаючі коливання.