3. Вычисление температурного поля

Для расчета температурного поля на стадии предельного состояния используется программа, составленная на языке Бейсик или программа MathCAD. Оценка тепловой обстановки в области действия сварочного источника выполняется на поверхности тела размерами 210100 мм.

Для конкретных параметров режима сварки плавлением и теплофизических свойств свариваемого металла определяем Т(х, у)_ПР для следующих значений х · 10^-3 мм: 10, 5, 0, -5, -10, -15, -20, -25, -30, . . . , -200. Для каждого "х" расчет проводим при следующих значениях у · 10^-3 мм: 0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50.

Результаты вычислений температуры для случаев 1 и 2 сводят в табл. 3.1.

Таблица 3.1

х, мм	± у, мм
	0	5	10	15	20	25	30	35	40	45	50
15
10
5
0	∞
-5
-10
….
-200

При вычислении Т(r,x,z) для схемы плоского слоя (случай 3) по формуле (2.5.) по значениям r/δ , δ/(2a) определяют, используя номограмму рис. 22 величину коэффициента "m", на поверхности (z = 0) и корневой плоскости (z = δ) плоского слоя. Результаты вычислений сводятся в табл. 3.2.

Таблица 3.2

х, мм	± у, мм
	0	5	10	15	20	25	30	35	40	45	50
15	r/δ Т
10
5
0	∞
-5
-10
….
-200

Примечание: для конкретной координаты "х" в верхней строке таблицы указано текущее значение r/δ, а в нижней – соответствующая величина Т.

По полученным данным, используя номограмму для определения коэффициента "m", заполняется таблица 3.3. предельных значений температуры на поверхности (z = 0) и корневой плоскости (z = δ) плоского слоя.

Таблица 3.3

х, мм	± у, мм
	0	5	10	15	20	25	30	35	40	45	50
15	т(z,0)·ТПР т(z,δ)·ТПР
10
5
0	∞
-5
-10
…
-200

По полученным данным (таблица 3.1-3.3) на бумаге формата А4 строим графики температурного поля (рис. 21):

Т₁(x, y, z)=f₁(x) для y·10^-3: 0, 10, 20, 30, 50 мм;

Т₂(x, y, z)=f₂(±y) для x·10^-3: 0, -10, -20, -50, -100 мм.

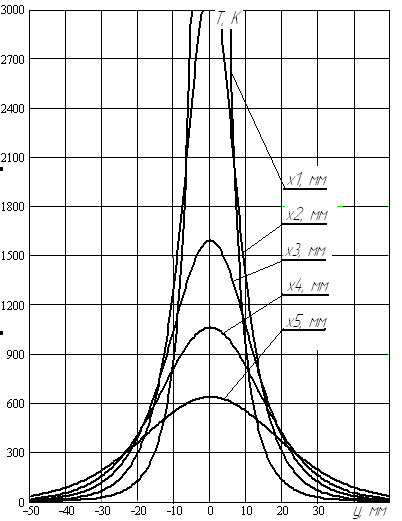
а б

Рис. 21. Распределение температур в плоскостях, параллельных осям х (а) и у (б)

Рис. 22. Номограмма для определения коэффициента т(r,z)