ВВЕДЕНИЕ

Большинство существующих способов сварки основано на нагреве материала до пластического состояния или плавления. Необходимую для этой цели теплоту получают от источников энергии, которые различаются между собой по характеру выделения теплоты, мощности, продолжительности действия, скорости движения и другим признакам. Свариваемые изделия различают по свойствам материала и геометрическим размерам. Если принять во внимание условия, при которых происходит сварка, - подогрев, искусственное охлаждение, теплоотдачу, количество независимых параметров, подлежащих учету в расчетах тепловых процессов при сварке, окажется довольно значительным.

Один из основных вопросов, рассматриваемых в теории тепловых процессов при сварке, - определение условий, при которых достигается необходимый нагрев изделия и его сваривание. Нагрев и охлаждение вызывают разнообразные физические и химические процессы в материале изделия - плавление, кристаллизацию, структурные превращения, объемные изменения, появление напряжений и пластических деформаций. Эти процессы приводят к глубоким изменениям свойств и состояния материала, влияют на качество всей конструкции в целом. Чтобы определить характер протекания указанных процессов, необходимо знать распределение температур в теле и изменение его во времени в каждом отдельном случае. Это второй основной вопрос, рассматриваемый в теории тепловых процессов при сварке.

Теория тепловых процессов при сварке является частью общей теории теплопроводности в материалах. Она использует ряд понятий и законов, известных из теории теплопроводности, применяя их к специфическим условиям сварки.

1. Тепловые процессы при сварке

1.1. Схемы нагреваемого тела.

Формы тел, нагреваемых при сварке, весьма разнообразны. Распространение теплоты существенно зависит от формы и размеров тела. Точный учет конфигурации тела может привести к таким усложнениям расчета, что его практическое использование окажется затруднительным. Поэтому во всех тех случаях, когда пренебрежение второстепен­ными особенностями формы тела не приводит к большим погрешностям расчета, целесообразно упрощать формы рассматриваемых тел, сводя их к простейшим. Разумеется, грамотное применение такой схематизации должно основываться на четком понимании физической сущности процесса в целом. Обычно вы­бирают одну из следующих основных схем.

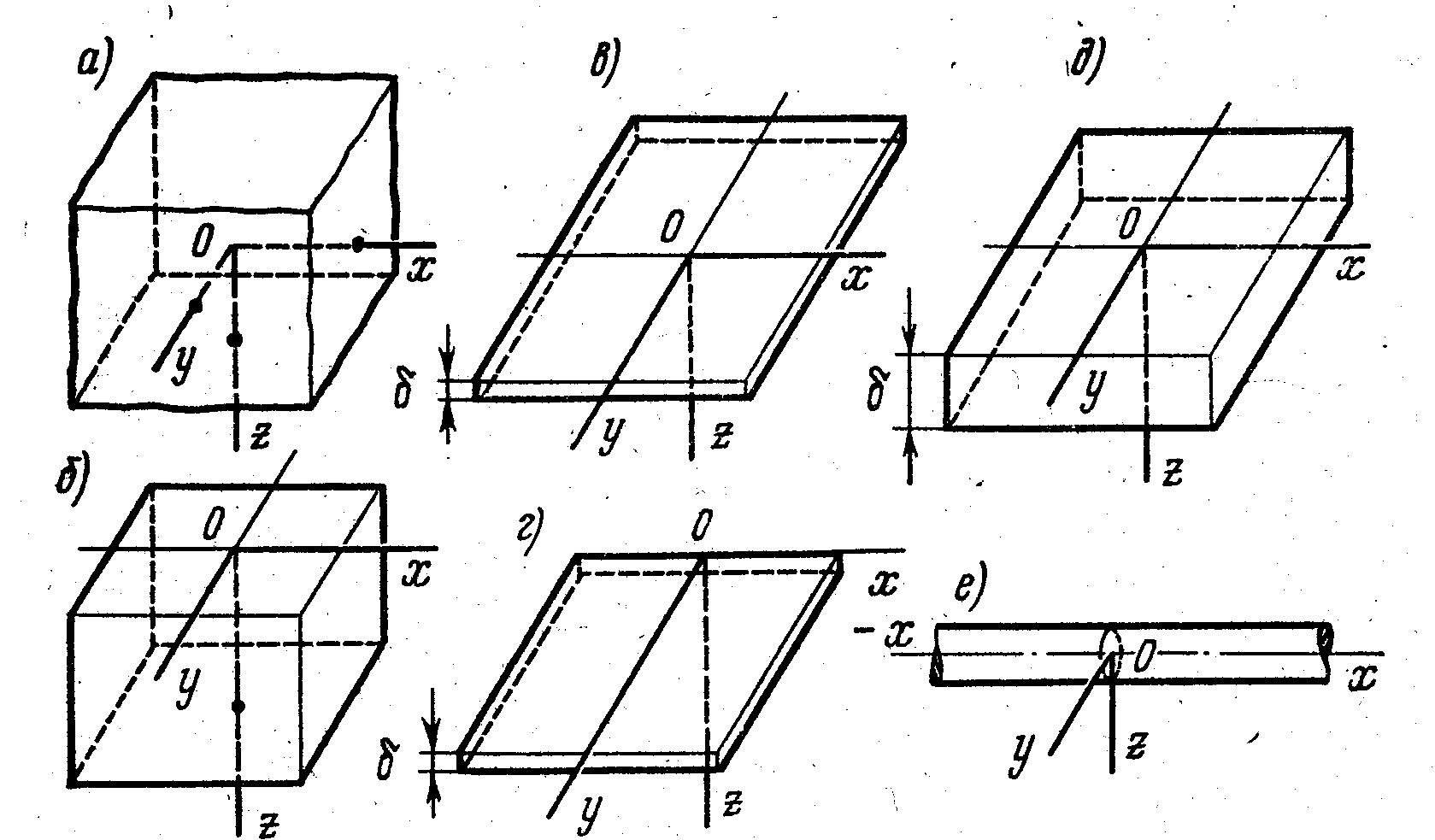
Рис.1. Расчетные схемы тел

Бесконечное тело. Если границы тела не влияют на распространение теплоты, его можно заменить бесконечным телом, у которого имеется неограниченная протяженность по всем трем направлениям х, у, z (рис. 1, а).

Полубесконечное тело. Этой схеме соответствует массивное тело с одной ограничивающей плоскостью z = 0 (рис. 1, б). Остальные поверхности находятся на значительном удалении и не влияют на распространение теплоты.

Бесконечная пластина представляет собой тело, ограниченное двумя параллельными плоскостями z=0 и z=. При использовании этой схемы всегда предполагают, что температура по толщине листа равномерна, а теплота может распростра­няться только в плоскости с координатными осями х и у (рис. 1, в).

Полубесконечная пластина представляет собой тело, ограниченное двумя параллельными плоскостями z = 0 , z =  и плоскостью у = 0 (рис. 1, г). Остальные условия те же, что и у бесконечной пластины.

Плоский слой представляет собой пластину, у которой температура точек тела по толщине не является равномерной. Эту схему применяют в тех случаях, когда толщина тела не настолько велика, чтобы можно было пренебречь влиянием ограничивающей плоскости z =  и считать тело полубесконечным (рис. 1, д).

Бесконечный и полубесконечный стержни представляют собой тела с прямолинейной или криволинейной осью, когда температура равномерна в пределах поперечного, сечения стержня (рис.1, е).

Помимо названных схем, в практике расчетов используются также и другие простейшие схемы, например сплошной цилиндр, тонкостенный цилиндр. В приведенных схемах тел могут использоваться как декартовы, так и цилиндрические или полярные координаты.

1.2. Основные теплофизические величины, понятия и определения.

Теплота - это форма движения материи. Количество теплоты Q в системе СИ измеряется в джоулях.

Удельное количество теплоты (теплосодержание) h, (Дж/кг) выражает количество теплоты, сообщенное телу массой 1 кг, при нагреве его от температуры Т₁, до температуры Т₂ . При технических расчетах теплосодержание тела, отсчитывают от 0° С, а не от абсолютного нуля. Вне критических точек теплосодержание в металлах с ростом температуры возрастает монотонно. В критических точках, соответствующих аллотропическим и фазовым превращениям, происходящим с поглощением или выделением теплоты, оно изменяется скачкообразно (рис.2). Удельная теплота фазового превращения l (Дж/кг) определяется, как количество теплоты, поглощаемой или выделяемой единицей массы материала при изотермическом процессе фазового превращения: l = L /m.

Истинная удельная массовая теплоемкость с (Дж/кг∙град) есть количество теплоты, необходимое для изменения на один градус температуры единицы массы тела (рис. 2). В расчетах бывает удобно пользоваться средней удельной массовой теплоемкостью в данном интервале температур от Т₁ до Т₂:

В расчетах может использоваться истинная С и средняя С_m удельная объемная теплоемкость Дж/(м³·град), которая связана с массовой удельной теплоемкостью следующими соотношениям

С=с , С_m=с_m  , (1.1)

где -плотность (кг/м³) в нормальных физических условиях.

В критических точках вследствие скачкообразного изменения теплосодержания использование истинной теплоемкости не имеет смысла.

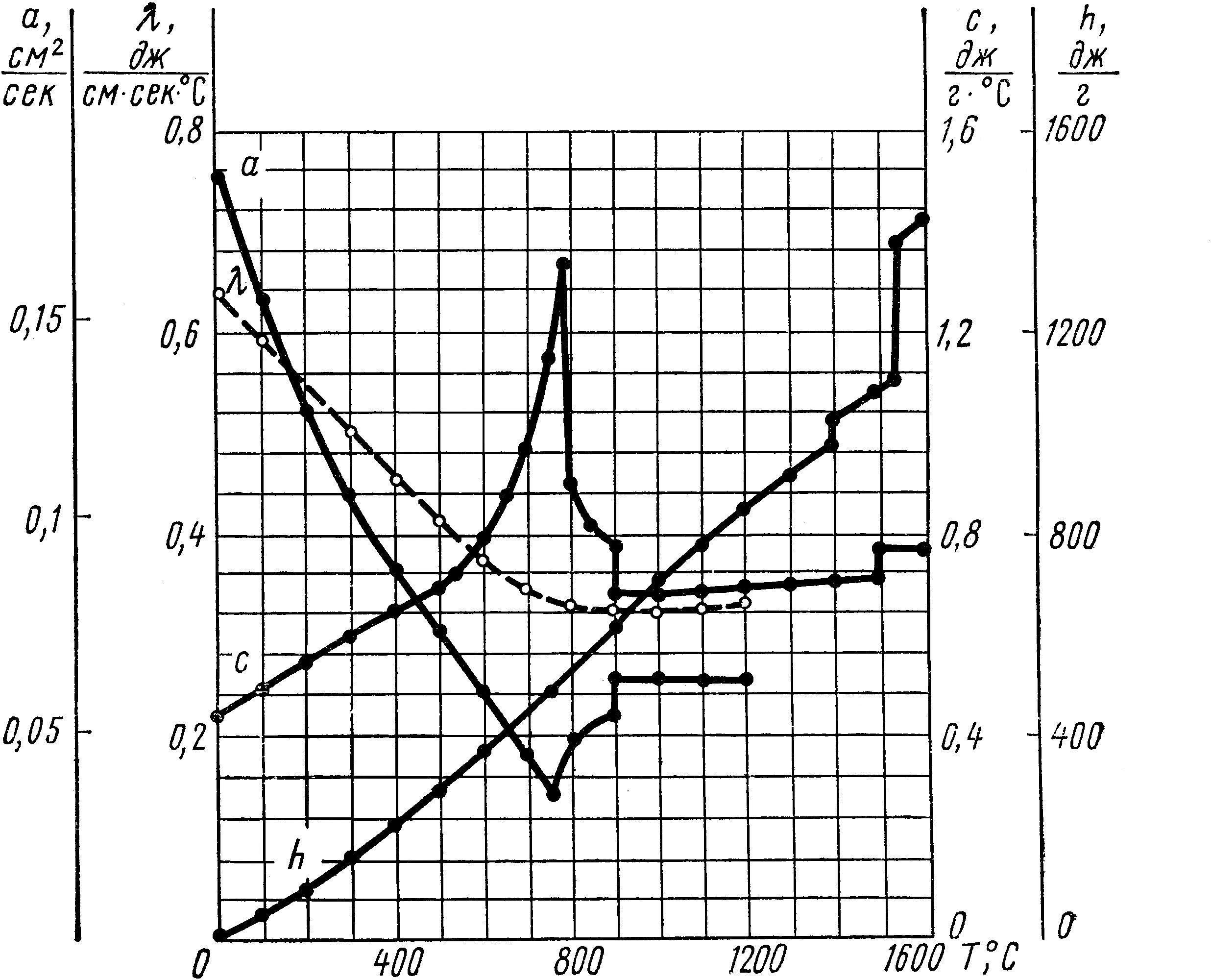
Рис. 2. Теплофизические свойства малоуглеродистой стали с 0,1% С: теплосодержание h; истинная теплоемкость с; коэффициент теплопроводности ; коэффициент температуропроводности а в промежутке температур 0-1600°С

Температурное поле есть распределение температур в теле в конкретный момент времени. Температура в общем случае может являться не только функцией координат х, у,z отдельных точек, но и функцией времени T=T(x,y,z,t).

В последнем случае температурное поле является объемным. Оно может быть также плоским T=T(x,y,t) или линейный T=T(x,t).

Для наглядности температурные поля часто представляют графически в виде изотерм (рис.3, а).

Изотермической поверхностью или изотермической линией называется геометрическое место точек тела, имеющих одинаковую температуру (рис.3, б).

Рис. 3. Изображение температурного поля изотермами:

а - изменение температуры по направлению SS;

б - касательная tt и нормаль nn к изотерме.

От точки к точке температура тела может изменяться. Изменение температуры в направлении SS на длине бесконечно малого отрезка dS называется градиентом температуры в рассматриваемой точке по данному направлению SS. Математически градиент температуры выражается как частная производная Т по направлению SS:

grad T_SS =  T / S.

Наибольший градиент температуры в точке имеется по на­правлению нормали пп к изотерме (рис. 3, б).

Скорость изменения температуры в данной точке поля с координатами x₀ , y₀ , z₀ в данный момент времени t₀ выра­жается частной производной от температуры по времени:

Тепловой поток - это количество теплоты, проходящее через рассматриваемое сечение (поверхность) в единицу времени: Ф = dQ/dt . Тепловой поток измеряется в ваттах. Удельный тепловой поток определяется тепловым потоком, приходящимся на единицу площади: q₂ = dФ/dS .

Коэффициент теплопроводности  характеризует свойство тел проводить теплоту. Численно коэффициент  выражает количество теплоты, протекающее через единицу изотермической поверхности в единицу времени, если изменение температуры по направлению нормали составляет 1 град на 1 м. Теплопроводность металла существенно изменяется в зависимости от температуры и химического состава материала. На рис. 4 показано изменение  в зависимости от температуры. Величина  измеряется в Вт/(м∙ град) или в Дж/(м∙c∙град).

Рис. 4. Коэффициент теплопроводности различных марок стали в зависи­мости от температуры: 1 - электролитическое железо; 2 - малоуглеродистая сталь 0,1% С; 3 - углеродистая сталь 0,45% С; 0,08% Si, 0,07% Мn; 4 - низколегиро­ванная хромистая сталь 0,10% С, 0,02% Si, 0,4% Мn, 4,98% Сr; 5 - хромистая сталь 1,52% С, 0,39% Si, 0,38% Мn, 13.1% Сr; 6 - хромоникелевая нержавеющая сталь 18-8.

1.3. Поверхностная теплоотдача и краевые условия

Выше были сформулированы условия теплопередачи в твердых телах вследствие теплопроводности металлов. С поверхности металлов теплота передается конвективным путем или посредством радиации. Указанные процессы играют важную роль при сварке - в конечном итоге вся теплота, введенная при сварке, отдается в окружающее пространство и тела остывают.

Конвективный теплообмен. При конвективном теплообмене теплота с поверхности уносится жидкостью или газом, которые перемещаются относительно поверхности. Движение жидкости или газа может возникать вследствие различной плотности нагретых и ненагретых зон или в результате принудительной циркуляции жидкости и газа.

Приближенно тепловой поток q_2k вт/м² с единицы поверхности за единицу времени при конвективном теплообмене опреде­ляется по правилу Ньютона:

q_2k =_к(T-T₀), (1.2)

где _к - коэффициент конвективной теплоотдачи, дж/(с·м·град); Т - температура поверхности твердого тела, град; То - температура жидкости или газа, град.

Коэффициент _к не является постоянной величиной, он за­висит от многих факторов и может изменяться в широких пре­делах в зависимости:

• от свойств окружающей среды (теплопроводности, плотности, вязкости) и ее движения относительно поверхности;

• от физических свойств теплоотдающей поверхности;

• от формы поверхности тела и ее положения в пространстве;

• от разности температур Т-То.

Лучистый теплообмен. Тепловое излучение, возникающее в теле вследствие тепловой энергии, представляет собой электромагнитные колебания. Удельный поток излучения тела пропорционален четвертой степени его абсолютной температуры (закон Стефана - Больцмана):

, С= Со. (1.3)

Коэффициент С зависит от состояния поверхности тела и выражается через коэффициент степени черноты тела . Для абсолютно черного тела  = 1, а С=Со=5,76 дж/с∙м²∙К⁴. Большинство встречающихся в технике тел можно рассматривать как серые тела, у которых  < 1. Величина  зависит от природы тела, характера поверхности и температуры. Для окисленных шероховатых поверхностей сталей  изменяется от 0,6 до 0,95. У алюминия  изменяется от 0,05 до 0,2 в зависимости от обработки поверхности и температуры.

В реальных условиях нагретое тело окружено другими телами (помещение цеха, сварочные приспособления, изделия и др.). Между этими телами происходит взаимный лучистый теплообмен. Каждое тело излучает энергию и воспринимает часть энергии, излучаемой другими телами:

, (1.4)

где Т - температура тела, град; Т_о - температура окружающих тел, град.

Первое слагаемое в уравнении выражает теплоту, излучаемую телом, второе - поглощаемую теплоту.

По аналогии можно связать удельный тепловой поток q_2r с разностью температур Т-То:

q_2r =_r(T-T₀), (1.5)

где _r - коэффициент лучистого теплообмена, Дж/(с·м²·град).

Тогда удельный поток полной теплоотдачи можно представить как сумму удельных потоков конвективного и лучистого теплообмена:

q₂ =_k(T-T₀)+ _r(T-T₀)= (T-T₀), (1.6)

где =_k+_r - коэффициент полной поверхностной теплоотдачи.

При температурах до 200…300 °С значительная часть теплоты отдается конвективным теплообменом, при более высоких температурах - в основном лучистым теплообменом (рис. 5).

Краевые условия. Чтобы рассчитать изменение температуры точек тела во времени, недостаточно знать закономерности распространения теплоты в теле, необходимо еще привлечь два условия:

• условия теплообмена на границах тела - граничные условия;

• распределение температуры в теле при t=0.

Рис. 5. Коэффициент полной теплоотдачи вертикальных листов  и коэффициент лучистого теплообмена _r в зависимости от температуры (углеродистая сталь)

Граничные условия выражают тепловое взаимодействие поверхности тела с окружающей средой и могут быть весьма разнообразны. С практической точки зрения интересны следующие граничные условия.

Условия 1-го рода. Граничное условие 1-го рода определяет закон изменения температуры точек поверхности тела. Частным случаем условия 1-го рода является изотермическое условие, когда поверхность тела обладает постоянной температурой в течение всего процесса распространения теплоты. Например, при интенсивном омывании поверхности тела жидкостью температура поверхности может оставаться постоянной. В расчетах тепловых процессов при сварке условие 1-го рода встречается относительно редко.

Приведем пример того, как можно с помощью некоторых формальных приемов удовлетворить изотермическому условию Т = 0. Пусть полубесконечная пластина нагревается в точке О сварочной дугой (рис. 6, а), а граница А - А постоянно поддерживается при температуре Т = 0. Очевидно, что если бы пластина была бесконечной, то распределение температур в сечении 1-1 в некоторый момент времени выражалось кривой 1 и температура по линий А - А не равнялась нулю. Однако, можно пред­ставить, что в той же бесконечной пластине в точке О - находя­щейся также на расстоянии L от А - А, действует источник теплоты с отрицательным знаком, так называемый сток теплоты. Причем свойства этого стока теплоты в точности совпадают со свойствами источника теплоты от сварочной дуги, а распреде­ление температур описывается одинаковым математическим выражением.

Тогда отрицательная температура выражается кривой 1’, аналогичной кривой 1, но с отрицательным знаком. Складывая ординаты кривой 1’ с ординатами кривой 1, получим кривую 2 распределения температуры. На границе А - А температура всегда будет равна нулю, в то время как в самой пластине температура точек будет непрерывно меняться.

Рис. 6. Выполнение граничных условий: а - изотермического путем использования сто­ка теплоты; б - адиабатического путем исполь­зования дополнительного источника теплоту.

Условие 2-го рода определяет величину теплового потока на границе тела. Если вспомнить, что закон теплопроводности Фурье выражает связь между тепловым потоком и градиентом температур, то станет понятным, что условие 2-го рода задает градиент температуры на границе тела.

Адиабатическая граница является частным случаем условия 2-го рода, когда тепловой поток с поверхности тела равен нулю, т. е.

q_s = 0; . (1.7)

В технических расчетах, в частности применительно к сварке, нередко встречаются случаи, когда тепловой поток, с поверхности тела мал по сравнению с потоками внутри тела. Тогда мож­но принять эту границу как адиабатическую.

Например при нагреве сварочной дугой полубесконечной пластины в точке О (рис. 6, б) граница А - А соприкасается с воздухом и излучает некоторое количество теплоты. Для простоты расчетов можно принять, что граница А - А является теплонепроницаемой, т. е. адиабатической. Выполнить это условие можно, пользуясь формальным приемом. Допустим, что пластина является бесконечной и в ней на расстоянии L по другую сторону от линии А - А в точке O₁ действует точно такой же источник теплоты, как и в точке О. Очевидно, что тепловой поток через границу А - А от источника О равен в каждой точке линии А - А тепловому потоку от источника О₁ . Суммарный тепловой поток через границу А - А, следовательно, равен нулю. Температура точек полубесконечной пластины находится путем сложения ординат кривой 1 с ординатами кривой 1’ (рис. 6, б). Температура края полубесконечной пластины оказывается вдвое больше температуры соответствующих точек бесконечной пластины. Описанный прием компенсации теплового потока носит название метода отражения, так как в этом случае теплонепроницаемая граница может рассматриваться как граница, отражающая тепловой поток, идущий со стороны металла.

Условие 3-го рода определяет теплообмен на границе тела и среды с заданной температурой. По правилу Ньютона

q_2s =(T_s -T₀), (1.8)

где q_2s - удельный тепловой поток через граничную поверхность; Т_s - температура точек поверхности тела; То - температура среды.

Очевидно, что по закону теплопроводности к границе поступает теплота при этом q_2s = q₂ .

Из условия 3-го рода, как предельные случаи, могут быть получены изотермическое и адиабатическое условия. Если  - некоторая конечная, не равная нулю величина, то при    име­ем изотермическое условие, а при   0 - адиабатическое.

1.4. Источники теплоты.

Нагрев тел может производиться разнообразными источниками теплоты, различающимися между собой по распределенности, времени действия и движению их относительно тела. При определенных условиях все многообразие источников тепло­ты можно получить, пользуясь мгновенным точечным источником теплоты.

Мгновенный точечный источник теплоты - понятие абстракт­ное. Физической схемой, примерно воспроизводящей мгновенный точечный источник, является случай, когда в очень малый объем за весьма малый промежуток времени введено некоторое коли­чество теплоты q. Формально такое введение теплоты можно рас­сматривать как граничное условие при t = 0, когда вместо рас­пределения температур задается распределение теплоты в теле. Действительно, если принять, что во всех точках тела, кроме одной, теплосодержание равно нулю, а в точке скоординатами x₀, y₀, z₀ при t = 0 содержится количество теплоты q, то будем иметь случай мгновенного точечного источника.

В последующие моменты времени теплота будет распространяться по телу, подчиняясь уравнению теплопроводности.

Процесс распространения теплоты в бесконечном теле в этом случае будет выражен следующим уравнением:

, (1.9)

где Т - температура в рассматриваемой точке с координатами х; у; z; t - время, отсчитываемое с момента введения теплоты; - расстояние до рассматриваемой точки от начала координат, где была введена теплота q.

При t = 0 во всех точках, где R  0, имеем T = 0. В точке R = 0 при t = 0 имеем T  . Правильность выбора постоянного множителя в уравнении доказывается путем вычисления интеграла, выражающего количество теплоты во всем объеме бесконечного тела. Это количество в любой момент времени равно q, так как тело не отдает теплоты в окружающее пространство.

Изотермические поверхности представляют собой сферы.

Убывание температуры по радиусу выражается множителем , в то время как множитель описывает убывание температуры точки R = 0 во времени. Наибольшая температура всегда в точке R = 0.

Если теперь воспользоваться принципом наложения, то, комбинируя мгновенные точечные источники, можем получить множество иных источников теплоты. Принципом наложения можно пользоваться при условии, что теплофизические коэффициенты принимают независящими от температуры, а выделением и поглощением теплоты в процессе фазовых превращений пренебрегают. Принцип наложения заключается в сложении температур от действия отдельных источников, которые либо находятся в разных точках тела, либо выделяют теплоту в различные моменты времени, либо и находятся в разных точках тела и выделяют теплоту не одновременно.

Мгновенный линейный источник теплоты. Представляет собой комбинацию мгновенных точечных источников, действующих одновременно и расположенных по линии. Распределение q по линии действия ряда мгновенных точечных источников может выражаться различными функциями. Равномерное распределение q по линии (рис. 7, а) означает действие мгновенного линейного источника. В случае распределения q по нормальному закону (рис. 7, б) имеем нормально-линейный мгновенный источник.

Температурное поле в пластине, от мгновенного линейного источника при отсутствии теплоотдачи получается путем интегрирования температурных полей от мгновенных точечных источников

. (1.10)

Р ис. 7. Расчетные схемы источников теплоты: а - линейный источник в пластине; б – нормально линейный источник; в - плоский источник в стержне; г - нормально круговой источник на поверхности полубесконечного тела

После преобразований и замены q₁ = q/z находим

, (1.11)

где - плоский радиус-вектор (расстояние от рассматриваемой точки до мгновенного источника теплоты); t – время отсчитываемое от момента начала действия мгновенного источника.

Температурное поле симметрично относительно оси z. Теплота распространяется относительно оси z равномерно в плоскости хОу.

Мгновенный плоский источник теплоты представляет собой совокупность мгновенных точечных источников теплоты, действующих одновременно и расположенных в одной плоскости. Распределение теплоты q при t = 0 может иметь разнообразный характер. Под мгновенным плоским источником обычно понимают равномерное распределение q по сечению (рис. 7, в). В слу­чае нормального распределения q по кругу имеем мгновенный нормально-круговой плоский источник (рис. 7, г).

Температурное поле от мгновенного плоского источника q₂ = q/F в стержне без теплоотдачи выражается уравнением

. (1.12)

Температурное поле является линейным, температура зависит только от координаты х и времени t.

Мгновенный объемный источник теплоты представляет собой совокупность мгновенных точечных источников, распределенных по какому-либо закону в теле.

Используя принцип наложения, удается получить различные мгновенные источники, отличающиеся по распределенности.

По существу только точечный источник является сосредоточенным по отношению ко всем координатным осям. Линейный источник является сосредоточенным по отношению к двум координатным осям и распределенным в третьем направлении. Плоский источник является сосредоточенным лишь в одном направлении. Объемный источник может служить примером распределенного источника по всем направлениям.

Н

9

епрерывно действующие источники теплоты представляют собой совокупность мгновенных источ­ников, распределенных по промежутку времени действия источника. Например, точечный источник может действовать непре­рывно в течение определенного отрезка времени t. В этом случае он уже не является мгновенным, так как теплота выделяется в точке постепенно.

Источники теплоты могут быть неподвижные, подвижные и быстродвижущиеся. Очевидно, что подвижный источник не может быть мгновенным, так как предполагается, что его движение протекает в течение некоторого отрезка времени, когда выделяется теплота. Точечный непрерывно действующий источник, продвигающийся из точки О в направлении х (рис. 8), яв­ляется подвижным источником. Для быстродвижущихся источников характерен ряд особенностей, которые рассмотрены далее.

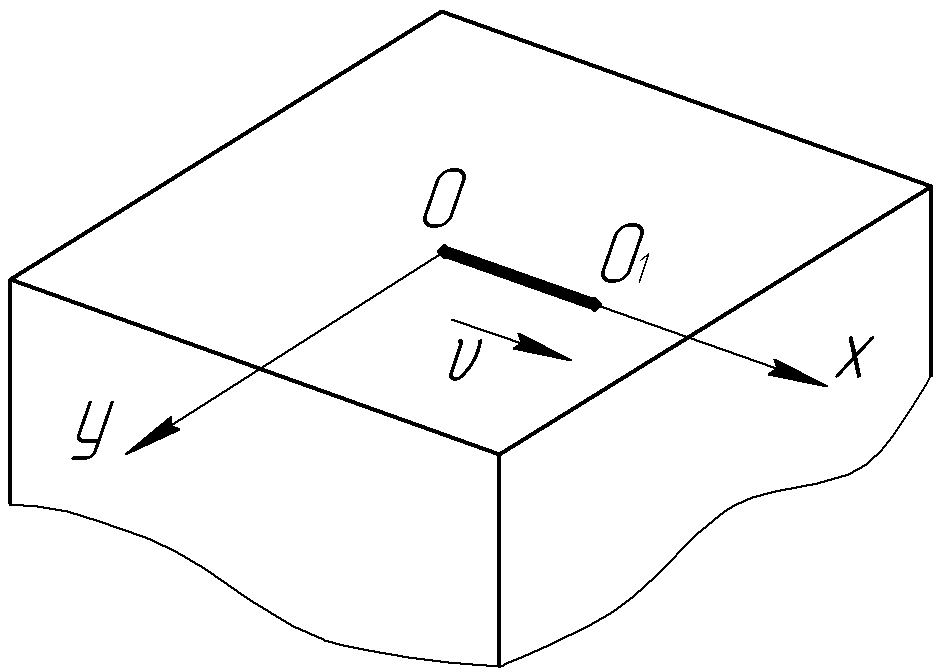
Рис. 8. Подвижный точечный источник на поверхности полубесконечного тела

1.5. Сварочные источники теплоты

Для процесса нагрева и сваривания материала существенным является также распределенность тепловых потоков, идущих от источника теплоты к свариваемому телу. Различные источники обладают различной распределенностью тепловых потоков, которая может также изменяться во времени в процессе сварки. В отношении теплового воздействия на свариваемые тела сва­рочные источники можно условно разделить на две группы:

1. Источники, тепловой поток которых практически мало меняется в течение всего процесса сварки. Это электрические дуги с различной защитой, газовое пламя перемещающегося источника, источники при электрошлаковом процессе, электроннолучевой сварке, контактной роликовой сварке и некоторые другие.

2 . Источники, тепловой поток которых и его распределение изменяются в течение процесса сварки. В качестве примеров таких источников можно привести источники при сварке стержней сопротивлением или оплавлением, точечной сварке, сварке трением и др.

Источники первой группы обладают определенным распределением удельного теплового потока, который мало изменяется во времени. Распределение удельного теплового потока может наблюдаться как по поверхности металла, так и в направлении его толщины.

Электрическая дуга и газовое пламя. Распределение удельного теплового потока источников теплоты по поверхности нагреваемых тел.

Теплота сварочной дуги или газового пламени от единичной горелки вводится на некотором участке поверхности металла диаметром d_H, называемом пятном нагрева (рис. 9). Удельный тепловой поток q₂ в пределах пятна нагрева крайне неравномерен. Наибольший удельный тепловой поток наблюдается в средней части пятна, по мере приближения к краям он резко убывает. Такое распределение потока объясняется наличием активного пятна в дуге и неравномерным распределением температур в пределах факела газового пламени.

Как показали исследования Н. Н. Рыкалина, М. X. Шоршорова и И. Д. Кулагина, распределение удельного теплового потока q₂ в направлении радиуса r для газового пламени и дуг, не углубленных значительно в ванну металла, можно прибли­женно описать кривой Гаусса (нормальным законом)

q₂ = q_2mexp(-kr²), (1.13)

где q_{2m -} наибольший тепловой поток в центре пятна нагрева, Вт/см²; k - коэффициент сосредоточенности теплового потока источника, 1/см²; r - радиальное расстояние данной точки от оси, см.

Источник с распределением теплового потока по приведенному выше закону называется нормально-круговым. Численные значения q_2m и k подбирают так, чтобы распределение теплового потока по уравнению наиболее близко соответствовало фактическо­му распределению, которое определяется опытным путем.

Существует определенная связь между законом нормального распределения теплового потока и эффективной мощностью q источника теплоты. Очевидно, что интегрирование удельного теп­лового потока по всей нагреваемой поверхности F должно дать эффективную тепловую мощность

. (1.14)

При использовании в расчетах обычно принято считать радиусом пятна нагрева расстояние r_н = d_н/2 , на котором удельный тепловой поток q₂(r_н) равен 0,05q_2m. Отсюда следует, что

q₂ (r_н) = q_2mexp(-kr_н²) = 0,05q_2m.

exp(-kr_н²) = 0,05; kr_н² = 3,0.

Условный расчетный диаметр, пятна нагрева

. (1.15)

Зная эффективную мощность источника и коэффициент сосредоточенности теплового потока k, можно судить о распреде­лении теплоты по поверхности металла и размерах пятна нагрева.

Опытами установлено, что с увеличением тока увеличивается наибольший удельный тепловой поток q_2т, а k уменьшается; с повышением напряжения дуги наибольший удельный тепловой поток и коэффициент сосредоточенности уменьшаются. Дуга, горящая в парах металла под флюсом, обладает более высокими значениями коэффициента сосредоточенности, чем от­крытые дуги (рис. 10).

Газовое пламя обладает малой проникающей способностью. Практически можно считать, что теплота газового пламени распределена лишь по поверхности.

Сварочные дуги обладают значительно большей проникающей способностью, в особенности при сварке под флюсом. Благодаря погружению дуги в металл удается сваривать под флюсом за один проход стальные листы толщиной до 40 мм. Проникающая способность дуги зависит не только от характера ее защиты, но и от рода тока и его частоты.

Газовое пламя при одинаковой мощности с дугой обладает значительно меньшим максимальным удельным тепловым потоком q_2т и значительно меньшей сосредоточенностью k. Представление о соотношениях k, d_н и q_2т у газового пламени и дуги дает рис. 11.

Рис. 10. Распределение удельных тепловых потоков

сварочных дуг по радиусу

Рис.11. Сравнение распределений удельных тепловых потоков дуги и пламени, близких по эффективной мощности q: а - угольная дуга, поверхностная, постоянного тока, прямой полярности I = 190 А; U = 32 В и пламя горелки с наконечником № 3: С₂Н₂ = 400 л/ч; q=3000…3300 Дж/с; б - металлическая дуга, поверхностная, переменного тока, I=550 A, U=37,5 B и пламя горелки с наконечником №7, С₂Н₂ =2600 л/ч; q= 9400…9900Дж/с.

Опытные данные о проникающей способности дуги и пламе­ни в глубину металла немногочисленны, особенно в отношении распределения теплоты по глубине металла.

Схемы источников теплоты, которые используются в расчетах тепловых процессов при дуговой и газовой сварке, зависят от распределения теплового потока источника теплоты, от размеров рассматриваемой области тела по сравнению с размерами пятна нагрева и от теплофизических свойств свариваемого материала.

Газовое пламя в силу своей специфической особенности давать значительное распределение теплоты по нагреваемой поверхности обычно заменяют источником с нормальным распределением теплоты (рис. 12, а). При сварке листов небольшой толщины можно принимать, что распределе­ние теплоты в радиальном направлении также подчиняется нормальному закону, а в направлении толщины - равномерно (рис. 12, б).

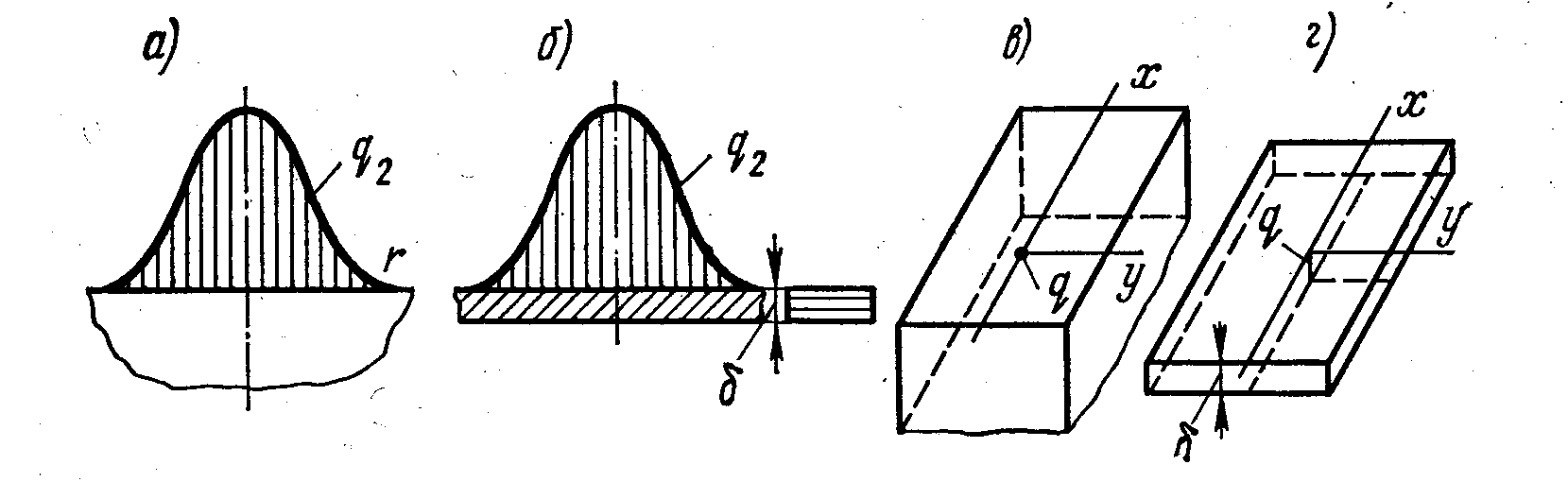
Рис. 12. Расчетные схемы выделения теплоты при нагреве тел сварочными источниками теплоты: а - газовое пламя, полубесконечное тело; б - газовое пламя, пластина; в - дуга, полубесконечное тело; г - дуга, пластина

Сварочную дугу чаще представляют как сосредоточенный источник теплоты. При сварке на поверхности массивного тела, в соответствии с принципом местного влияния, процесс распространения теплоты дуги в области, не слишком близкой к пятну дуги, рассчитывают в предположении, что источник теплоты точечный (рис. 12, в). При дуговой однопроходной сварке листов встык считают, что источник теплоты линейный (рис. 12, г).

Схематизация источников теплоты значительно упрощает расчеты, но не позволяет правильно определять температуры вблизи источника в области, размеры которой близки к размерам пятна нагрева.

Электронный луч. Электроннолучевой источник теплоты относится к наиболее концентрированным. Распределение потока энергии вносимого через плоскость листа металла, перпендикулярную к лучу, в первом приближении также может выражаться нормальным законом. Однако эта энергия луча превращается в тепловую не на плоскости листа, а в глубине металла при торможении электронов. При сварке листов металла относительно небольших толщин тепловыделение по толщине листа практически равномерно; при увеличении толщины свариваемого материала наблюдается некоторая неравномерность ширины провара с сужением у корня шва.

Световой луч. Световой луч, получаемый от лазера, является наиболее концентрированным источником теплоты, используемым при, сварке. Энергию луча удается концентрировать на площадках размером в несколько микрон. Энергия излучается короткими импульсами, что обычно приводит к испарению металла из зоны сварки. Диаметр площади проплавления в результате действия одного импульса луча лазера составляет десятые доли миллиметра. Между импульсами имеются длинные паузы.

1.6. Влияние режима сварки и теплофизических свойств металла на поле температур

Рассмотрим влияние скорости сварки и эффективной мощности источника теплоты на температурное поле предельного состояния при сварке пластин.

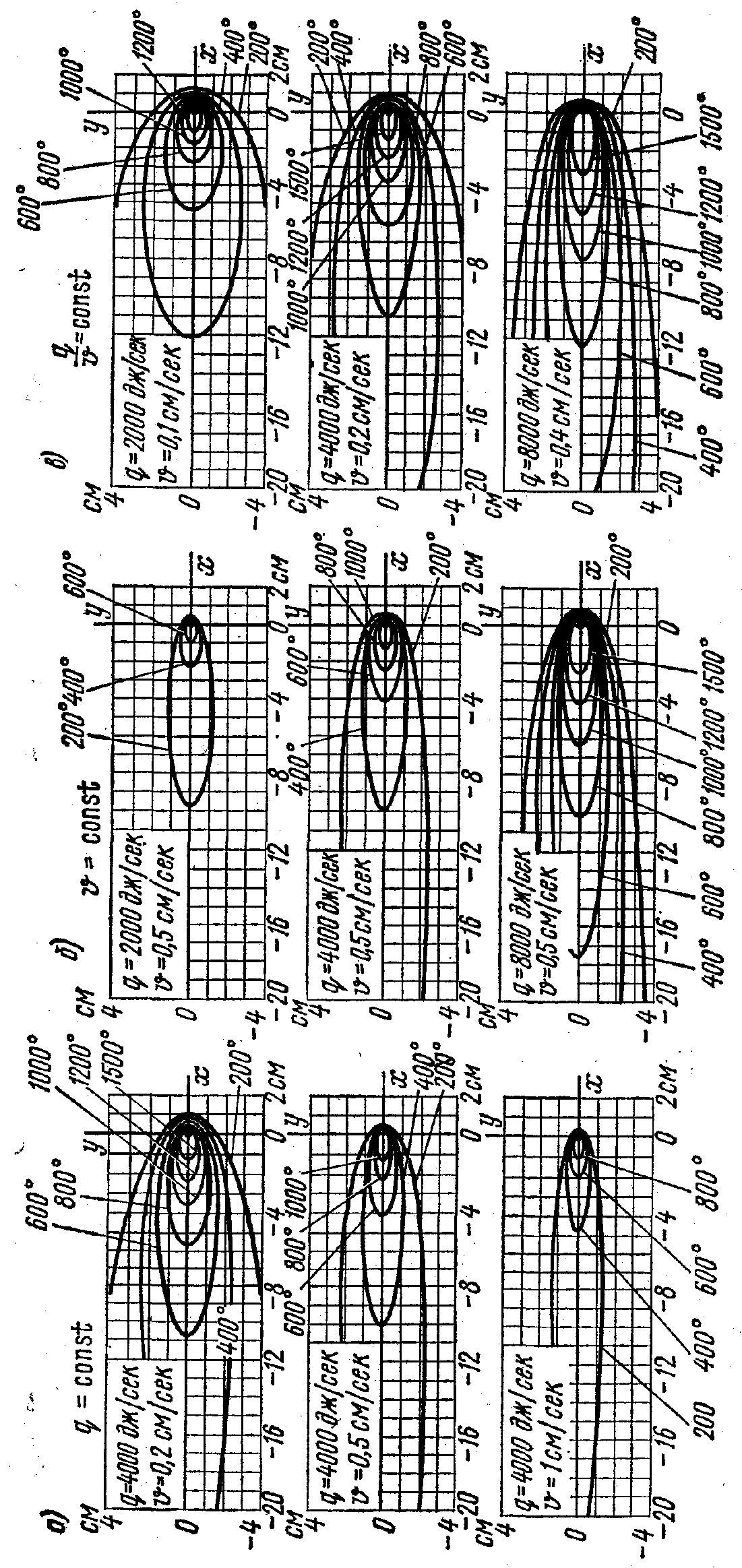
С увеличением скорости  при q=const изотермы, соответствующие определенным температурам, например Т=600 °С, уменьшаются по ширине и длине (рис. 13, а). Если пренебречь коэффициентом температуроотдачи, то окажется, что уменьшение длины и ширины изотерм происходит прямо пропорционально увеличению скорости сварки.

С возрастанием мощности источника теплоты области, нагретые выше определенной температуры, увеличиваются по длине и ширине значительно быстрее мощности источника. Увеличение длины изотерм идет быстрее, чем ширины (рис. 13, б). Одновременное увеличение мощности источника теплоты и скорости сварки при постоянной погонной энергии - сварки приводит в основном к увеличению длины изотерм. Ширина изотерм также увеличивается, но стремится к определенному значению (рис. 13, в).

Теплофизические свойства металла также оказывают существенное влияние на поле температур.

Наиболее заметно влияет теплопроводность металлов . Увеличение теплопроводности при прочих равных условиях примерно соответствует случаю одновременного уменьшения мощности и скорости при постоянной погонной энергии сварки. Изотермы сильно укорачиваются по длине и несколько сужаются по ширине. В качестве примера можно сравнить между собой малоуглеродистую и аустенитную стали, у которых теплоемкости примерно одинаковы, а теплопроводность различная (рис. 14, а, б). У меди и алюминия, обладающих высокой теплопроводностью, изотермы в области высоких температур близки к окружностям (рис. 14, в, г).

Увеличение теплоемкости металла с оказывает примерно такое же влияние, как увеличение скорости сварки при постоянной мощности. С увеличением теплоемкости металла при прочих равных условиях изотермы укорачиваются и сужаются.

Рис. 14. Влияние теплофизических свойств на характер температурного поля в пластине толщиной 10 мм; q=4200 Дж/с; =2 мм/с

При сварке массивных тел влияние параметров режима сварки и свойств металла на поле температур иное, чем при сварке пластин.

Изменение скорости сварки при q=const в основном влияет на ширину изотерм и почти не влияет на их длину. По оси шва в области позади источника теплоты, где R = -х, распределение температуры не зависит от скорости.

Поэтому с увеличением скорости сварки изотермы сгущаются впереди источника теплоты, а распределение температуры на отрицательной полуоси остается постоянным (рис. 15).

С увеличением мощности источника теплоты q увеличивается длина и ширина изотерм на плоскости хОу. Увеличение длины изотерм происходит быстрее, чем их ширины.

Одновременное увеличение мощности источника и скорости сварки при постоянной погонной энергии сварки q/ качественно влияет на форму и размеры так же, как и при сварке пластин.

Увеличение теплопроводности  равносильно одновременному уменьшению мощности источника и скорости сварки при постоянной погонной энергии q/. Увеличение теплоемкости с влияет так же, как возрастание скорости сварки, т. е. изотермы сужаются но распределение температуры по отрицательной полуоси остается постоянным.

Рис 15. Влияние  точечного источника теплоты на распределение температуры по оси Ох в полубесконечном теле:

q =4000 Дж/сек;  = 40 Дж/мсград; а = 8∙10^-6 м²/с

1.7. Ширина зоны нагрева

Для оценки термического влияния на свариваемый металл бывает необходимо определить размеры зоны 2l, нагревавшейся выше заданной температуры Т_l (рис. 16). В общем случае ширина зоны нагрева выше температуры Ти определяемая величиной 2l, будет найдена, если определить координату у точки А. Точка А, во-первых, находится на изотерме и, следовательно, имеет температуру Т_l во-вторых, в точке А достигается максимальная температура на расстоянии y=l, т. е. T/x=0. Таким образом, для определения ширины зоны необходимо решить систему двух уравнений.

Рис. 16. Ширина зоны 2l, нагревавшейся выше температуры Т_l.

Для мощного быстродвижущегося точечного источника теплоты на поверхности полубесконечного тела ширину зоны термического влияния можно определить из уравнения:

. (1.16)

Ширина зоны нагрева при сварке пластины определяется аналогично полубесконечному телу. Для мощного быстродвижущегося линейного источника теплоты в пластине при b=0 ширину зоны нагрева 2l определяют по формуле:

. (1.17)

Пример 1. На поверхность массивного тела наплавляется валик. Определить ширину зоны, нагревшейся выше 600С, при которой углеродистая сталь в значительной мере теряет упругие свойства. Режим: I = 400 A, U = 25 В, υ = 9 м/ч ( = 0,6). Теплофизические свойства: а = 0,08 см² /с; с = 4,9 Дж/(см³град).

Ширина зоны нагрева для источника на поверхности массивного тела определяется по формуле (1.16).

Мощность источника теплоты

q = U·I·η = 400 · 25 · 0,6 = 6000 Вт

Скорость источника υ = 9 м/ч = 0,25 см/с.

см.

Пример 2. Как влияет величина погонной энергии на размеры зоны термического влияния? В каком из 3-х случаев размер ЗТВ будет наименьшим и наибольшим для режимов дуговой сварки при прочих равных параметрах:

1 – I₁ = 200 A; U₁ = 28 В; υ ₁ = 7 м/ч.

2 – I₂ = 400 A; U₂ = 30 В; υ ₂ = 20 м/ч.

3 – I₃ = 450 A; U₃ = 31 В; υ ₃ = 25 м/ч.

Погонная энергия – отношение эффективной энергии источника теплоты (q) к скорости его движения (υ).

Зависимость ширины ЗТВ от отношения q/ υ описывается выражениями: для точечного источника на поверхности полубесконечного тела (1.16); для линейного источника в пластине (1.17).

Вариант 1: q/ υ = UI/ υ = 200·28/ 7 = 800

Вариант 2: q/ υ = UI/ υ = 400·30/20 = 600

Вариант 3: q/ υ = UI/ υ = 450·31/25 = 560

Ширина ЗТВ наибольшая в первом случае, наименьшая в третьем.

Пример 3. Тонкая пластина из низколегированной стали ( = 6 мм) проплавляется дугой на режиме: I = 350 A, U = 10 В, υ = 18 м/ч. Определить ширину зоны, нагревшейся выше 700°С (принять  = 0,6; с = 5 Дж/(см³град)).

Ширина зоны нагрева для линейного источника в пластине определяется по формуле (1.17).

Мощность источника теплоты

q = U·I·η = 350 · 10 · 0,6 = 2100 Вт

Скорость источника υ = 18 м/ч = 0,5 см/с.

см.

1.8. Термический цикл при однопроходной сварке и его основные характеристики. Максимальные температуры

В процессе однопроходной сварки источник теплоты перемещается в теле и вместе с ним перемещается температурное поле. Температуры точек тела непрерывно изменяются (рис. 17). Вначале температура повышается, достигает максимального зна­чения, а затем снижается. Изменение температуры во времени в данной точке тела называется термическим, циклом.

Рис. 17. Изменение температуры в точках А,В,С со временем

При установившемся температурном поле термические циклы точек, расположенных на одинаковом расстоянии от оси движе­ния источника теплоты, являются одинаковыми, но смещены во времени.

Термические циклы точек, расположенных на различных рас­стояниях от оси движения источника теплоты, различаются меж­ду собой. В более удаленных точках температура повышается медленнее и позже достигает максимального значения.

Восходящая ветвь температурной кривой называется стадией нагрева, спадающая ветвь - стадией остывания.

Основными характеристиками термического цикла являются: максимальная температура, скорость нагрева и скорость охлаж­дения, а также длительность пребывания материала выше задан­ной температуры. Эти характеристики цикла зависят от режима сварки, теплофизических свойств материала, конфигурации тела, условии его охлаждения, температуры предварительного подо­грева.

Максимальные температуры, достигаемые отдельными точка­ми, определяются просто, если известно температурное поле. В точке максимальной температуры первая производная по вре­мени или по расстоянию равна нулю: T/t=0; T/x=0.

Производная по времени или по расстоянию берется в зави­симости от того, какую координату содержит выражение для температурного поля. Время t и координата х, как известно, свя­заны между собой скоростью сварки.

Аналитическое определение максимальной температуры в мас­сивном теле и в пластине сопряжено с трудностями. Максимальную тем­пературу аналитически выразить не удается. Возможно числен­ное определение максимальной температуры, которое по существу состоит в построении участка термического цикла. Если необходимо определить максимальную температуру в точке, находя­щейся на расстоянии у₀ от оси движения источника теплоты, то задаются несколькими отрицательными значениями х₀, подстав­ляют х₀ и у₀ в соответствующие формулы, находят температу­ры и строят график термического цикла в зависимости от х₀. Координату z₀ в уравнении для полубесконечного тела полагают равной нулю.

1.9. Мгновенная скорость охлаждения при данной температуре

Определение скорости охлаждения может представ­лять интерес, когда изменение скорости охлаждения в интервале температур распада аустенита может вызвать существенное из­менение механических свойств металла. Например, при сварке закаливающихся материалов путем изменения режима сварки и термического цикла можно заметно уменьшить степень закалки отдельных зон и тем самым снизить вредные последствия, вызванные термическим циклом сварки.

Мгновенная скорость охлаждения  является первой произ­водной температуры по времени

=T/t. (1.18)

Ее определение, в общем случае, производят следую­щим образом. По формулам для расчета тепловых полей в пластине или полубесконечном теле находят координа­ты точки, расположенной в интересующей зоне и имеющей темпе­ратуру, при которой требуется определить скорость охлаждения. Затем значения этих координат подставляют в формулу скорости охлаждения (1.18).

Так как в большинстве случаев оказывается достаточным при­ближенное определение скорости охлаждения, то используют теорию мощных быстродвижущихся источников теплоты без уче­та теплоотдачи. Скорости охлаждения определяют только для оси шва, ввиду их незначительного отличия от скоростей охлаждения околошовных зон, нагревавшихся до Т=800…900° С и выше.

Скорости охлаждения точек оси шва при наплавке валика на массивное тело при однопроходной сварке пластин встык с учетом начальной температуры находим из формул для быстродвижущихся источников при r=0 и y=0.

массивное тело ; (1.19)

пластина . (1.20)

где T₀ - начальная температура изделия или температура со­путствующего подогрева.

Знак минус в уравнениях (1.19) и (1.20) показывает, что происходит остывание металла. Скорость охлаждения зависит от формы изделия (массивное тело, пластина), эффективной погонной энергии и температуры подогрева.

Температура подогрева T₀ практически позволяет в большей степени регулировать скорость охлаждения, чем эффективная по­гонная энергия.

Влияние подогрева и погонной энергии сварки на скорость охлаждения резче сказывается в пластинах, чем в массивных телах. Это следует из показателей степеней в формулах (1.19) и (1.20).

Пример 1. Для случая наплавки углеродистой стали определить рекомендуемую погонную энергию, позволяющую избежать закалочные структуры без подогрева, если известно, что при 600°С критическая скорость охлаждения υ_охл = 35 °С/с (принять  = 38 Вт/(м  град). Какие параметры режима можно рекомендовать при υ=15 м/ч ?

Используем формулу для определения скорости охлаждения при наплавке на массивное тело (1.19).

Т = 600 ⁰С – температура, при которой определяется мгновенная скорость охлаждения, Т₀ = 0 ⁰С – наплавка без подогрева.

Скорость источника υ = 15 м/ч = 0,00417 м/с.

,

Вт.

Пример 2. Для случая наплавки массивного тела на режиме: I = 700 A, U = 35 В, υ = 20 м/ч рассчитать температуру предварительного подогрева (Т_о), позволяющую избежать появления закалочных структур, если известно, что допускаемая критическая скорость охлаждения при Т = 500 °С составляет 5 °С/с (принять  = 45 Вт/(м  град)).

Мощность источника теплоты (принимаем КПД η=0,8)

q = U·I·η = 700 · 35 · 0,8 = 19600 Вт.

Скорость источника υ = 20 м/ч = 0,00556 м/с.

Используем формулу для определения скорости охлаждения при наплавке на массивное тело (1.19), откуда

Т - Т₀ = 250

Т₀ = Т – 250 = 250 ⁰С.

В некоторых случаях необходимо найти длительность пребывания металла выше заданной температуры, показанную на рис. 18 отрезком t_н. Способ определения величины t_н с помощью термического цикла показан на рис. 18.

Рис.18. Схема термического цикла при однопроходной сварке.