1.9.1. Реальная покупательная способность денег

В рассмотренных выше финансовых схемах (расчет простых и сложных процентов, ренты, платы по векселям) все денежные единицы измерялись по номиналу, т.е. не принималось во внимание снижение их реальной покупательной стоимости за период, охватываемый операцией. Однако в современных условиях инфляция играет существенную роль.

Инфляцию следует учитывать в двух случаях: при расчете наращенных сумм и при оценке реальной доходности финансовой операции.

Введем обозначения:

S- наращенная сумма по номиналу. Она вычисляется по формуле (1.3)

S=P(1+ r n).

С - наращенная сумма с учетом ее обесценивания;

J_p — индекс цен;

J_c — индекс изменения покупательной способности денег за период. Значение наращивания с учетом обесценивания будет равно

С = S J_C. (1.5)

Индекс покупательной способности равен

1

J_{c = ----------------} (1.6)

J_p

Значит,

S

С=------- (1.7)

J_p

Индексы Jp, J_c должны относиться к одинаковым интервалам времени.

Пример 18

Пусть сегодня получено 150 тыс. руб. Известно, что за два предыдущих года цены увеличились в 1,5 раза (или произошло повышение цен на 50 %). Найти реальную покупательную способность денег.

Решение

S=150 000 руб. Индекс цен J_p =1,5, а индекс покупательной способности

1

J_c =-----------

1.5

Следовательно, по формуле (1.7) реальная покупательная способность S=150 тыс. руб. составит С=150/1,5=100 тыс. руб. в деньгах с покупательной способностью двухлетней давности.

1.9.2. Расчет темпа инфляции

Индекс цен связан с темпом инфляции. Под темпом инфляции h понимается относительный прирост цен за период (обычно в процентах).

h =100(J_р-1). (1.8)

Для предыдущего примера темп инфляции h =100(1.5-l)=50 %. Можно найти из (8.8) обратную зависимость -- индекс цен:

h

Jp = 1 + ----— . (1.9)

100

Например, если темп инфляции за период равен 30 %, то это означает, что цены выросли в 30

Jp = 1+ -----= 1,3 раз.

100

Инфляция является цепным процессом. (При расчете инфляции за текущий период нужно учитывать инфляцию за предыдущий период) Следовательно, индекс цен за несколько периодов равен произведению индексов цен:

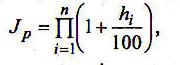(1.10)

где h_i - темп инфляции в периоде i.

Если h -постоянный ожидаемый (или прогнозируемый) темп инфляции за один период, то за t таких условий получим

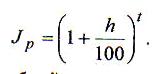(1.11)

Грубейшей ошибкой является суммирование темпов инфляции!

Пример 19

На следующий год прогнозируется постоянный темп инфляции в размере 5 % в месяц. Каков будет рост цен за год?

Решение

h= 5 %, t = 12 месяцев. Индекс цен по формуле (1.11) равен

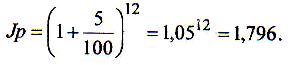
Т.е. годовой темп инфляции h= 100(1,796-1)=79,6 % (а при ошибочном суммировании 60 %!).

Пример 20

Приросты цен за три месяца составили: 1,5 %, 1,2 %, 0,5 %. Найти индекс цен и темп инфляции за три месяца.

Решение

h₁ =l,5%, h₂ =l,2%, h₃ =О,5%. По формуле (1.10) получим

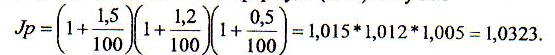
Значит, темп инфляции за три месяца равен

H =100(1,0323-1)=3,23%.