Конструктивный расчет арки.

Металлическая арка

1- расчет на устойчивость в плоскости действия изгибающего момента:

σ = [Nmax / φe∙А] ≤ Rу∙γc; γc = 0,95

---------------------------------------------------------------------------

п редварительно задаемся - φe =0,7÷0,8; λ=80;

находим площадь сечения - А

далее смотри схему расчета - рис 20.

Рис. 20

2 – проверка на прочность в плоскости действия изгибающего момента:

σ =(Nmax / А)+Mmax / Wx ≤ Rу∙γc;

3 – проверка на общую устойчивость:

(1,2÷1,3)Nmax ≤Nкр; Nкр = (π²∙E∙ IX)/ (μ∙S)²;

----------------------------------------------------------------------------------------------

При значительных нагрузках, больших пролетах и невозможностью применения сортамента из справочной литературы, для конструкции арки рекомендуется применять составные сечения из двутавров, швеллеров или уголков (см. рис.22 и 23).

Усилия в сквозных арках:

р ис.21

Nвп = - Mx / h - NX/ 2; Nнп = Mx / h - NX/ 2;

Nраскос. = Qx ∙(Cosφx / Cosβ); Nстойки = Qx ∙Cosφx;

Подбор и проверка сечения на прочность и устойчивость стержней арки производится по аналогии расчета стержней ферм на центральное сжатие:

σ = [Nmax / φ∙А] ≤ Rу∙γc;

После проверки сечения стержней сквозной арки производится снова расчет ее на устойчивость и прочность в плоскости действия изгибающего момента, а также на общую устойчивость (см.п.1,2,3-металлическая арка).

Сечения сквозных арок:

Геометрические характеристики некоторых сечений: - радиусы инерции (i), моменты инерции (J) и моменты сопротивления (W) сечений.

W=(2∙J)/h J=A∙i²;

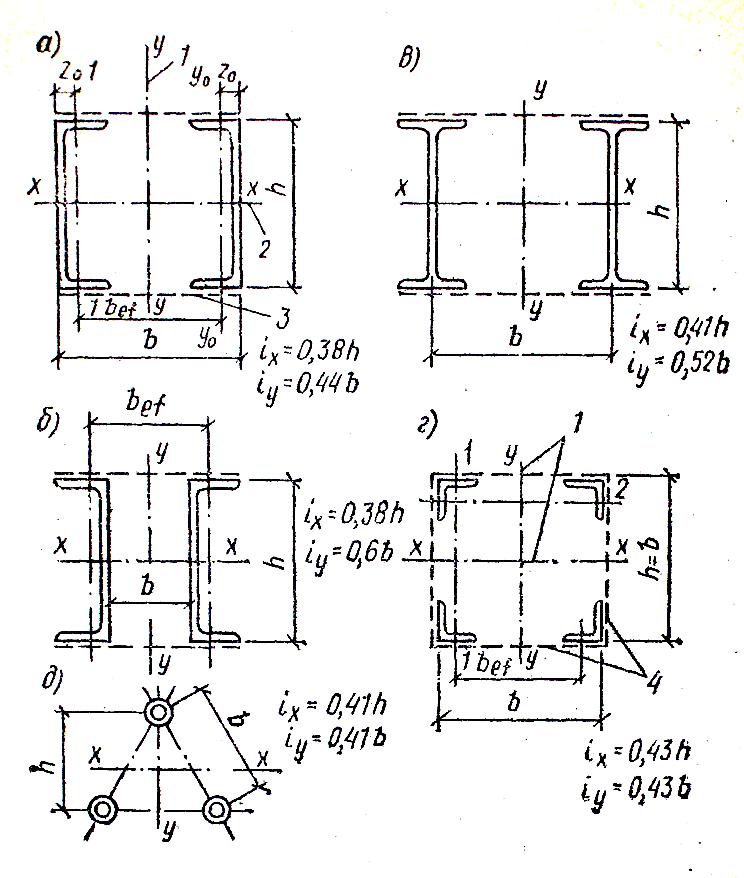Рис.22

Рис.23

Железобетонная арка 2 Железобетонная арка

Железобетонная арка

1- расчет на устойчивость в плоскости действия изгибающего момента:

Nmax ≤Nкр;

Nкр =(6,4∙Еб)/ (μ1∙Ѕ)²∙{(Jx/ Kдл)∙[0,11/(0,1+t)+0,1]+α1∙Js};

Тяжелый бетон	Еб- мПа, марка и класс прочности.
	М200	М250	М300	М350	М400
	В15	В20	В25	В27	В30
Естественного твердения	24∙10³	26,5∙10³	29∙10³	31∙10³	33∙10³
С теплой обработкой	21,5∙10³	24∙10³	26∙10³	28∙10³	30∙10³
Расчетное сопротивление сжатию по 1гр.пр. сост. Rb.	8,5	11,5	14,5	16,5	17

Jx –момент инерции бетонного поперечного сечения относительно оси х.

Js – момент инерции арматуры относительно центра тяжести бетонного сечения.

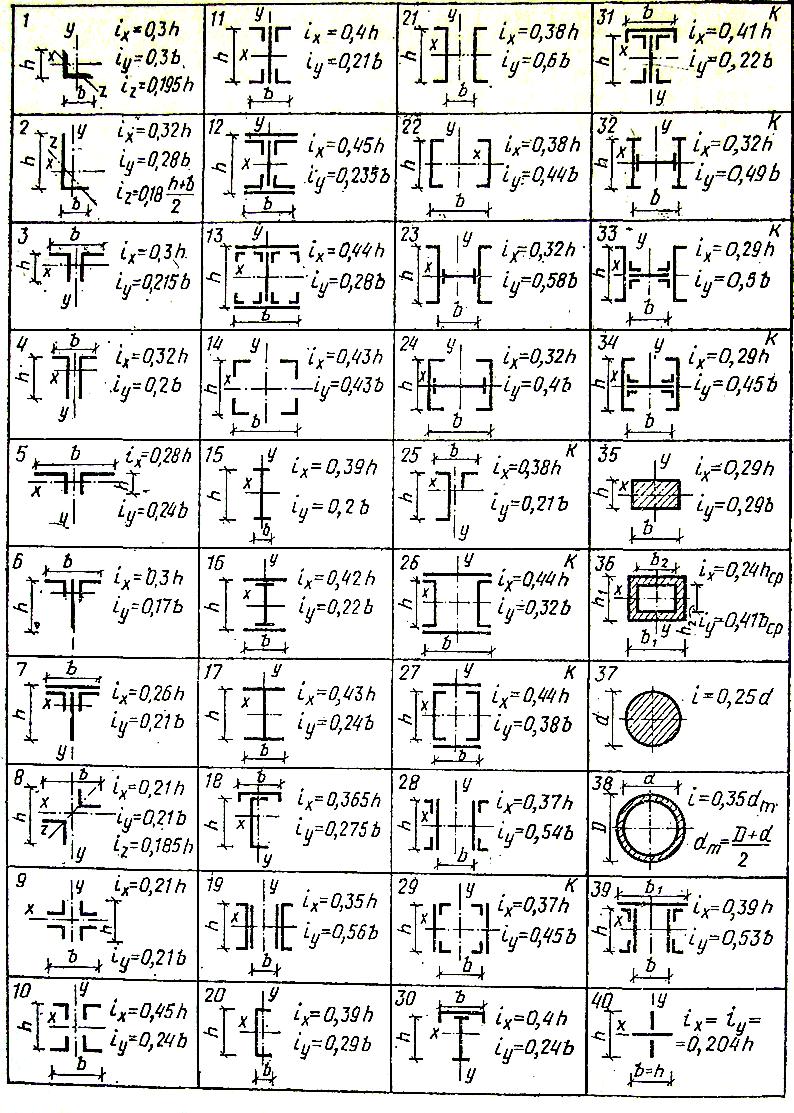
Jx =b∙h³/ 12; Js =As∙i²= As∙(h/2-a)²;

As =μ2∙b∙ h0;

Рис.24 μ2 =(As / Ab)∙100%≤3%.

ix=0,289h.

Jx =b∙ (H³ - h³)/ 12;

Js=μ2∙b∙(H –h)∙(0,5H –a)²; ix=0,5H-a. iу=0,5b.

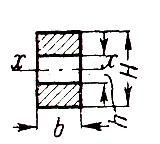μ2 =(As / Ab)∙100%≤3%.

Рис.25

Кдл=1+Мдл / M; Мдл – изгибающий момент от длительно

действующей нагрузки.

Кдл=2 - для упрощения расчетов.

{ t=e0/h; или t=0,5 - (0,01∙ μ1∙Ѕ) / h;}– выбирается tmax из двух значений t;

α1=Es / Eb;

сл сл сл сл сл л

e0= e′ + e0мах ; e′=М/ N; { e0 =S/600; или e0 =h/30; или e0 =1см;}– e0 мах выбирается из трех значений.

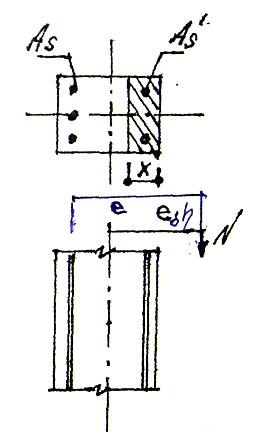
2- расчет на прочность при внецентренном сжатии:

μ1	Тип арки
0,58	3-х шарнирная
0,54	2-х шарнирная
0,36	бесшарнирная
μ1 – коэф. расчетной длины арки

при 4 ≤ λ = (μ1∙Ѕ)/ h ≤ 20; при λ = (μ1∙Ѕ)/ h > 20;

Рис.26	Рис.27	Рис.28
1- сжатие при случайном эксцентриситете: А's=[(N/φ∙Yc ) - Rb∙Ab]/Rs; Yc=1 при h > 200мм Yc=0,9 при h ≤ 200мм φ = φb+2∙( φsb –φb)∙Rs∙μ2/Rb≤ φsb для упрощения расчетов можно принять φ = 0,92 μ2 – коэф.армирования μ2 [( А's+ Аs )/ Ab]]∙100%. μ2=0,1÷3%. μ2 опт. =1÷2%.	2 - сжатие с малыми эксцентриситетами: ξ = X/h0 > ξR	3 - сжатие с большими эксцентриситетами: ξ = X/h0 ≤ ξR
	ξR – граничное значение относительной высоты сжатой зоны бетона ξR = ξ0 / [ 1+Ra∙ (1- ξ0 /1,1) / 400]; ξ0 =0,85 – 0,008Rb; ξ0 – характеристика сжатой зоны бетона. Ra –расчетное сопротивление арматуры растяжению, МПа. X=N/Rb ∙b;
	А's=Аs=[N∙e -Rb∙Ab∙(h0 – 0,5x)] / Rsc ∙(h0 – a);	А's= [N∙e -Rb∙ b∙h²0 ∙αR] / Rsc ∙(h0 – a′); При А's ≤0 ,то А's= μ2 min.∙ b∙h0; Аs=[(Rb∙ b∙h0 ∙ ξR – N) / Rs] + А's ; αR = ξR ∙(1 – 0,5 ξR);
		При бетоне класса прочности В30 и меньше принимать ξR =0,55; αR = 0,1
	e= e0∙ŋ + у ; cмотри ниже. у – расстояние от центра тяжести сечения арки до центра тяжести растянутой арматуры у=0,5h - a′

Ŋ – коэф. учета влияния прогиба на величину эксцентриситета продольного усилия.

Ŋ = 1/ [1 – N/Nкр]; 1< Ŋ ≤ 2,5

Nкр, e0 – cмотри стр.18

3- расчет металлической затяжки (необходим при опирании арки на колонны):

N ≤ Ra ∙Aa;

Ra – расчетное сопротивление арматуры растяжению.

Деревянная арка

1- расчет на прочность при внецентренном сжатии:

σ = N / Aнетто + MД / Wнетто ≤ Rc;

MД = M / KД; KД – коэф. учета дополнительного момента от продольной силы.

KД = 1 – N / φ∙Rc∙Aбрутто;

φ=3000/λ² - цельная древесина

λ>70

φ=2500/ λ² - клееная древесина

φ= 1-(λ/100)² - цельная древесина

λ ≤ 70

φ= 1-0,8∙( λ/100)² - клееная древесина

μ1∙S / ix =λ

Рис.29

μ1 =0,35 - двухшарнирная арка. μ1 =0,55 - трехшарнирная арка.

2- расчет на устойчивость в плоскости действия изгибающего момента:

N / φ∙Rc∙A + M / φт∙ W∙Rи ≤ 1;

φт =140∙b²∙Kф / μ1∙S∙h; - коэф. устойчивости для изгибаемых элементов прямоугольного постоянного поперечного сечения.

Rc – расчетное сопротивление древесины сжатию.

Rи - расчетное сопротивление древесины изгибу.

Kф – коэф. зависящий от формы эпюры изгибающих моментов.

Для расчета арок можно принять Kф =1,13;

Методика статического и конструктивного расчетов купола.

РАЗРЕЗ ЗДАНИЯ [вариант]

d

рис.1

план ЗДАНИЯ [вариант]

рис.2

Подсчет нагрузок на 1м2
Состав покрытия	qн н/м2	yf	q°н/м2
Вариант для ж/б гладкого купола
Оцинкованный кровельный лист
-0.001 мм, ρ=7850 кг/м3	78,5	1,1
Обрешетка из брусьев 40 х 40 ρ=500кг/м3	240	1,1
Стропила из досок 50 х 180 через 750	72	1,1
Шлакоизвестковая корка -30 ρ=1400кг/м3	420	1,3
Минеральный войлок -140 ρ=400кг/м3	560	1,2
Обмазочная пароизоляция ρ=1000кг/м3	10	1,3
ж/б купол -100 ρ=2500кг/м3	2500	1,3
Снег (при D≤50 М )		1,4
Снег (при D>50 М )		1,6
Бетон В30 ( м400); R=17МПа; Еб=33∙10³ МПа;
Вариант для ребристого, ребристо-кольцевого и сетчатого деревянного куполов .
Стекло оконное армированное -5мм
ρ=2500кг/м3	125	1,1
Обвязка (вариант) из фенольного стеклопластика-10мм	200	1,1
Обшивка (вариант) из полиэфирного
Стеклопластика-2мм	90	1,1
Обшивка (вариант) из водостойкой фанеры-10мм	160	1,1
Утеплитель из пенополистирола-50мм
ρ=100кг/м3	50	1,2
Пароизоляция-слой пергамина	40	1,2
Стальной профилированный настил	150	1,1
Собственный вес купола g=A∙ ρ/b1; A=a∙h; - сечение ребер. ρ – плотность материала. b1 – шаг ребер.
3-х слойный рулонный ковер	160	1,3
Щиты кровли при средней толщине досок -2,2см	111	1,1
Прогоны деревянные	140	1,1
снег		1,4

исходные данные:

тип купола

диаметр…

шаг ребер … шаг колец …

стрела подъема… тип кровли…

материал …

очертание… тип опор … снег … RУ - …

Rб - …

и т.п.

δплиты =d/600÷800-гладкий сферический купол (не менее 5см)…

δплиты =d/100÷150-гладкий конический купол (не менее 5см.) hребра= d/60÷100 ребристый купол… b1≤6м hребра= d/100÷150 ребристо-кольцевой купол hребра= d/300- сетчатый купол…(не менее 10 см.)

Определение геометрических размеров купола и усилий N1,N2,Nk).

Сферический гладкий купол.

Рис.3 рис.4

R=[ℓ²+4f² ] / 8f; - радиус кривизны. Sinφ = [ℓ-2X] / 2R; Cos φ = [Y+R – f] / R; ℓ –пролет. f – стрела подъема.

Y=√[R² –(0.5ℓ-X)² ] -R+f;– ордината.

Рис.5

пог o пог o

q =q ∙b; p = p ∙b; b=1м.

q p q пог p пог

N1= N1 + N1; N1 = q ∙R/(1+Cosφ); N1 = p∙ R/2;

q p q пог p пог

N2= N2 + N2; N2 = q ∙R∙[Cosφ -1/(1+Cosφ)]; N2= p ∙ R/2 ∙Cos2φ; q p q o p o

Nk= Nk + Nk; Nk = q ∙R² ∙[(1 –Cosφo)/tgφo ]; Nk=( p∙R² /4) ∙Sin2φo;

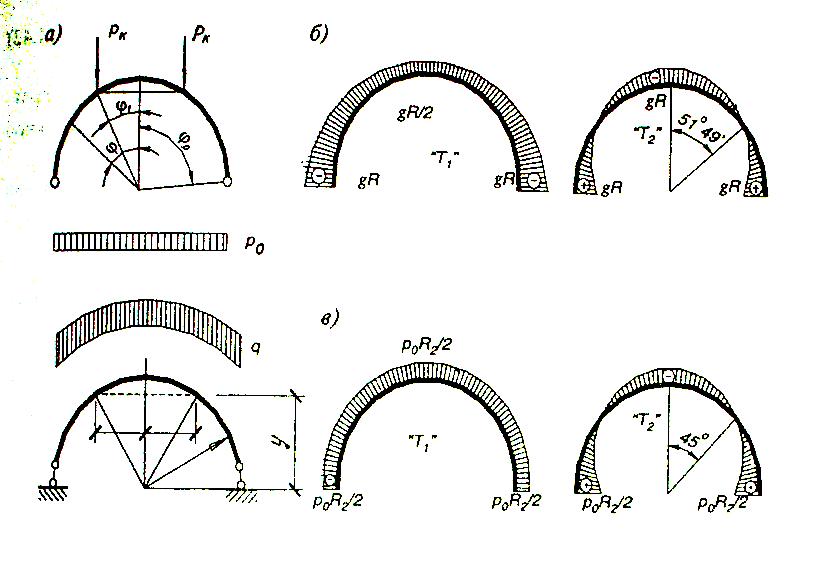q N2 = 0; при φ = 51, 83° или φ = 51° 49´

p

N2 = 0; при φ = 45°

Рис.6

Нахождение опорных реакций (в курсовой работе можно не выполнять).

p q p q

V= V + V; V=P°∙π∙R²∙Sin² φo; V= 2 π∙R²∙ q°∙(1 - Cosφo);

ребристый купол.

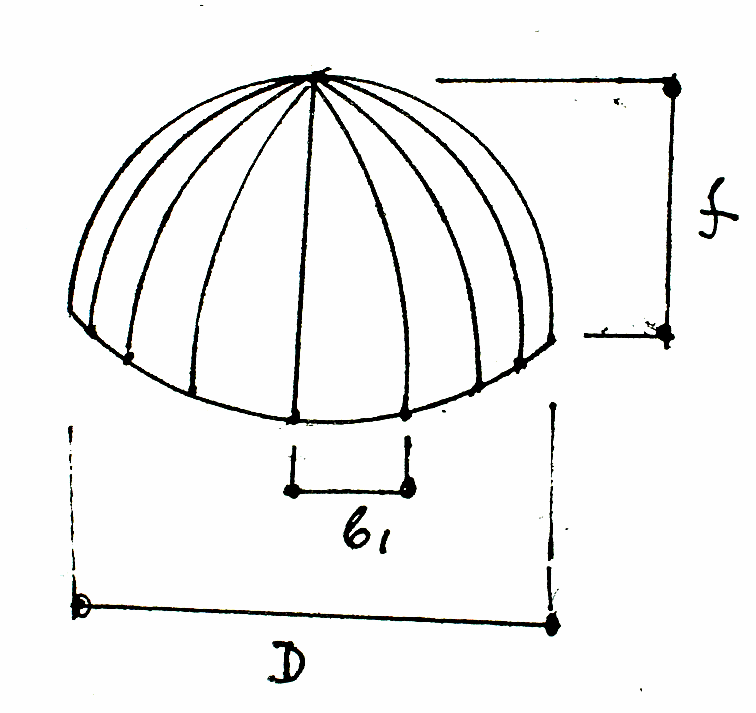Рис.7

пог пог пог пог

qобщая =q + p; q = q°∙b1;

пог

p = p°∙ b1;

q p

Nреб = N1 + N1;

q пог p

N1 = R∙q/(1+Cosφ); N1 = P∙R/2;

Пог

Nк = H∙D/2∙b1; H = qобщая ∙D²/24f;

Или Nк = H∙n/2π; n – число ребер. π=3,14; n= π∙D/ b1;

Определение опорных реакций V (в курсовой работе можно не выполнять).

Пог

V= qобщая ∙D/4; Sреб = π∙R∙n°/180°; R=( D² + 4f²)/ 8f;

или Sреб = 0,5∙√(D² + 16f²/ 3); R – радиус кривизны купола .

D – диаметр купола.

кн кв

S´реб = 2∙ π∙R∙( φo - φo )/ 180°;

рис.8

Ребристо-кольцевой купол.

(рассматривать совместно с формулами ребристого купола).

Рис.9

q p q пог

N2 = N2 + N2; N2 = q ∙R∙[Cosφ -1/(1+Cosφ)];

p пог

N2= p ∙ R/2 ∙Cos2φ; Nк, H, V – смотри ребристый купол.

сетчатый купол.

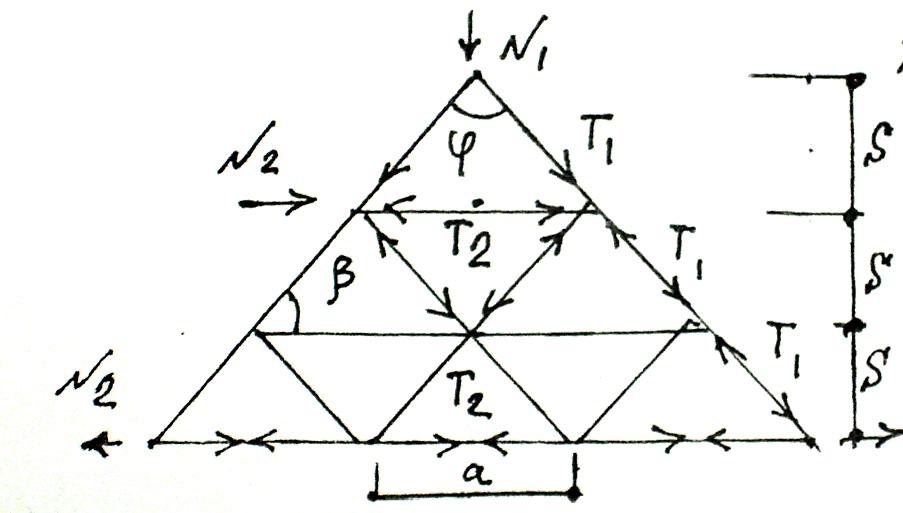Рис.10

T1 –продольное сжимающее усилие на единицу длины диагонального элемента.

T2 – усилие на единицу длины кольцевого элемента.

T1 = N1∙a/ 2Cos0,5φ; или T1 = N1∙a/ 2Sinβ;

T2 = N2 ∙ s; s,a – стороны ячейки сетчатого купола.

N1, N2, Nк, H, V – смотри ребристый и ребристо-кольцевой купола.

Конический и стрельчатый купола.

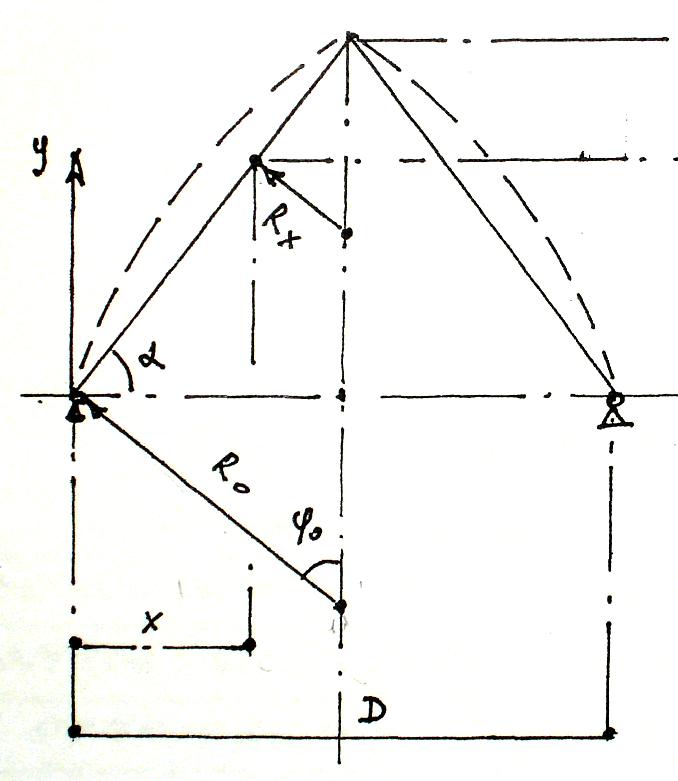
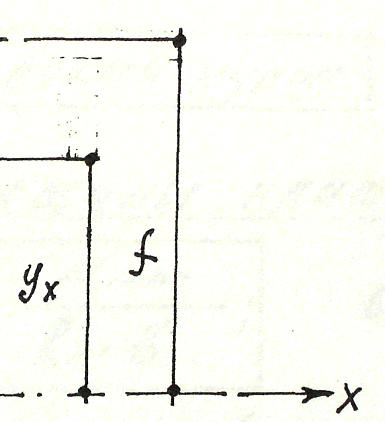
Рис.11

q p q пог p пог

N1= N1 + N1; N1,х = q ∙Rх/2∙Cosφ; N1,х = p∙ Rх/2;

q p q пог p пог

N2= N2 + N2; N2 = q ∙Rх∙Cosα; N2= p ∙ Rх ∙Cos²α;

q p q p

Nk= Nk + Nk; Nk = q° ∙Ro² ∙Sinα/ 2; Nk= p°∙Ro² ∙Sin2α/4;

φ = α – constant. В коническом куполе все кольцевые усилия N2 работают на растяжение.

Определение опорных реакций V (в курсовой работе можно не выполнять).

p q p q

V= V + V; V=P°∙π∙Ro²∙Sin²α; V= Ro²∙ q°∙Sin²α/ Cosα;

Конструктивный расчет купола.

ж/б гладкий сферический купол.

1. расчет на прочность с определением толщины плиты:

Рис.12

δпл = Nmax /Rb∙b; b = 1м. – ширина исследуемого участка плиты оболочки.

Nmax – выбирается из N1max и N2max (сжатие)/

В тонкостенных куполах сжимающие усилия воспринимаются полностью бетонным сечением. Поэтому армирование оболочки выполняется конструктивно – одиночными сетками, при δпл ≤ 70мм , Ø4÷6АΙ с шагом 150÷200мм. При δпл > 70мм, с целью уменьшения усадочных напряжений, устанавливаются 2 сетки с защитным слоем 15мм. Опорная зона испытывает краевой изгибающий момент (см.рис13 и 14, при шарнирном и жестком сопряжении плиты с опорным кольцом) и армируется двойными сетками с арматурой по расчетным формулам: (в курсовой работе можно не выполнять)

M1,min = - N'k ∙ R / 2k² ; M1,max = 0,208 M1,min; N'k = - Nmax ; - жесткий стык.

k = 1,316∙√(R∙/ δпл ); ℓk = π∙R / 2k; M1,max = 0,161 N'k∙ R / 2k² ; N'k = - Nmax ; ℓk = π∙R / 4k; - шарнирный стык.

α = M1,min / b∙h²o∙Rb ; α1 = M1,max / b∙h²o∙Rb ; α, α1 –смотреть ŋ по таблице

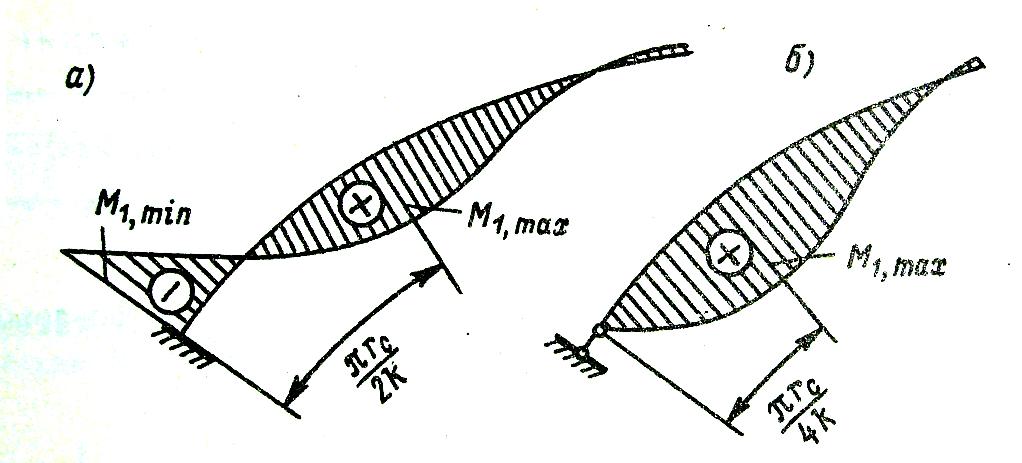As = M / ho∙ Rs ∙ ŋ; ho = δпл -15 мм.; в приложении стр.80

Рис.13

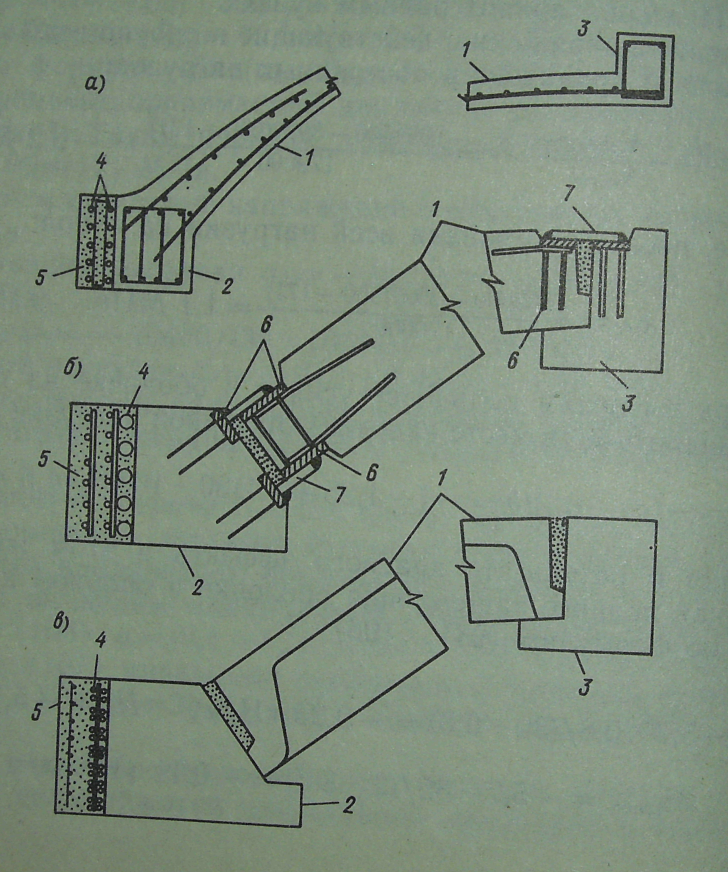
Рис.14

2. расчет на устойчивость плиты купола :

(Pº + qºс.в и кр.) ≤ (Eb / 15)∙( δпл / R)²;

Или δпл = √ [15∙ (Pº + qºс.в и кр.) ∙ R² / Eb ];

R – радиус кривизны. Eb – модуль упругости бетона.

3. расчет на прочность опорного кольца купола :

Ab = Nk/1,2∙Rb; As = Nk / Rs;

ж/б ребристый и ребристо-кольцевой купола.

Меридиональные ребра рассчитываются как внецентренно сжатые элементы по формулам, взятым из расчета арочных конструкций:

А's= [N∙e -Rb∙ b∙h²0 ∙αR] / Rsc ∙(h0 – a′);

При А's ≤0 ,то А's= μ2 min.∙ b∙h0;

Аs=[(Rb∙ b∙h0 ∙ ξR – N) / Rs] + А's ; При бетоне класса прочности В30 и меньше принимать ξR =0,55; αR = 0,1

e= e0∙ŋ + у ; у – расстояние от центра тяжести сечения арки до центра тяжести растянутой арматуры у=0,5h - a′

Ŋ – коэф. учета влияния прогиба на величину эксцентриситета продольного усилия.

Ŋ = 1/ [1 – N/Nкр]; 1< Ŋ ≤ 2,5

e0= e′ + e0мах ; e′=М/ N; { e0 =S/600; или e0 =h/30; или e0 =1см;}– e0 мах выбирается из трех значений.

Nкр =(6,4∙Еб)/ (μ1∙Ѕ)²∙{(Jx/ Kдл)∙[0,11/(0,1+t)+0,1]+α1∙Js};

Тяжелый бетон	Еб- мПа, марка и класс прочности.
	М200	М250	М300	М350	М400
	В15	В20	В25	В27	В30
Естественного твердения	24∙10³	26,5∙10³	29∙10³	31∙10³	33∙10³
С теплой обработкой	21,5∙10³	24∙10³	26∙10³	28∙10³	30∙10³
Расчетное сопротивление сжатию по 1гр.пр. сост. Rb.	8,5	11,5	14,5	16,5	17

Jx –момент инерции бетонного поперечного сечения относительно оси х.

Js – момент инерции арматуры относительно центра тяжести бетонного сечения.

Jx =b∙h³/ 12; Js =As∙i²= As∙(h/2-a)²;

As =μ2∙b∙ h0;

Рис.15 μ2 =(As / Ab)∙100%≤3%.

ix=0,289h.

Кдл=1+Мдл / M; Мдл – изгибающий момент от длительно

действующей нагрузки.

Кдл=2 - для упрощения расчетов.

{ t=e0/h; или t=0,5 - (0,01∙ μ1∙Ѕ) / h;}– выбирается tmax из двух значений t;

α1=Es / Eb; Sреб = π∙R∙n°/180°; R=( D² + 4f²)/ 8f;

или Sреб = 0,5∙√(D² + 16f²/ 3); R – радиус кривизны купола .

D – диаметр купола.

μ1	Тип сопряжения
0,54	шарнирное
0,36	жесткое
μ1 – коэф. расчетной длины ребра купола

Усилие N принимается максимальной от N1 или N2 (сжатых кольцевых ребер).

Подбор арматуры в растянутых кольцевых ребрах определяется по формуле:

As= N max / Rs;

ж/б сетчатый купол.

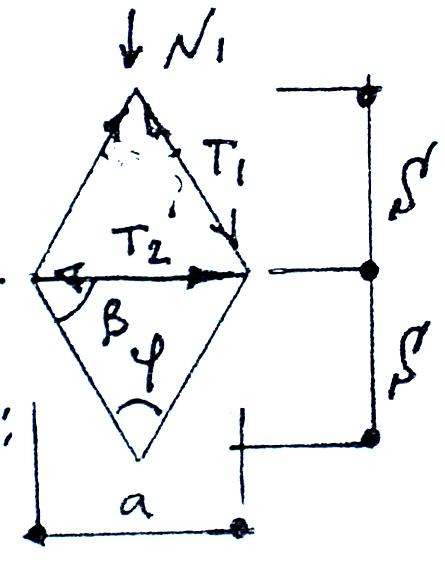Ребра ячеек, работающие на сжатие, рассчитываются по формулам на центральное сжатие:

Рис.16

А's=[(T1,2/φ∙Yc ) - Rb∙Ab]/Rsc; Yc=1 при h > 200мм

Yc=0,9 при h ≤ 200мм ; φ = φb+2∙( φsb –φb)∙Rs∙μ2/Rb≤ φsb

для упрощения расчетов можно использовать таблицу:

λ=ℓо/h	6	8	10	12	14	18	20
φ	0,92	0,91	090	0,89	0,87	0,84	0,74

μ2 – коэф.армирования. μ2= [( А's+ Аs )/ Ab]]∙100%.

μ2=0,1÷3%; μ2 опт. =1÷2%;

Стальной ребристый и ребристо-кольцевой купола.

Меридиональные и кольцевые ребра проверяют на устойчивость как внецентренно сжатые элементы:

σ = [Nmax / φe∙А] ≤ Rу∙γc; γc = 0,95

Стальной сетчатый купол.

Расчет на устойчивость сжатых ребер ведется по формулам на центральное сжатие:

σ = [Tmax / φ∙А] ≤ Rу∙γc;

Устойчивость сетки купола проверяют по формулам:

Tmax ≤ Tкр; Tкр = 0,8∙Ес∙А∙ix / Rкрив.;

Деревянный ребристый, ребристо-кольцевой и сетчатый купола.

Сжатые элементы куполов проверяются на прочность и устойчивость по формулам:

(смотри расчет деревянной арки стр.21 и 22)

σ = N / Aнетто + MД / Wнетто ≤ Rc;

N / φ∙Rc∙A + M / φт∙ W∙Rи ≤ 1;

Сетчатый купол дополнительно проверяется на общую устойчивость по формулам :

Tmax ≤ Tкр; Tкр = 0,8∙Ед∙А∙ix / Rкрив.;

Методика статического и конструктивного расчетов структурной плиты.

Плита с поясными сетками из квадратных ячеек

h=0,707∙s; при θº=45º

пог

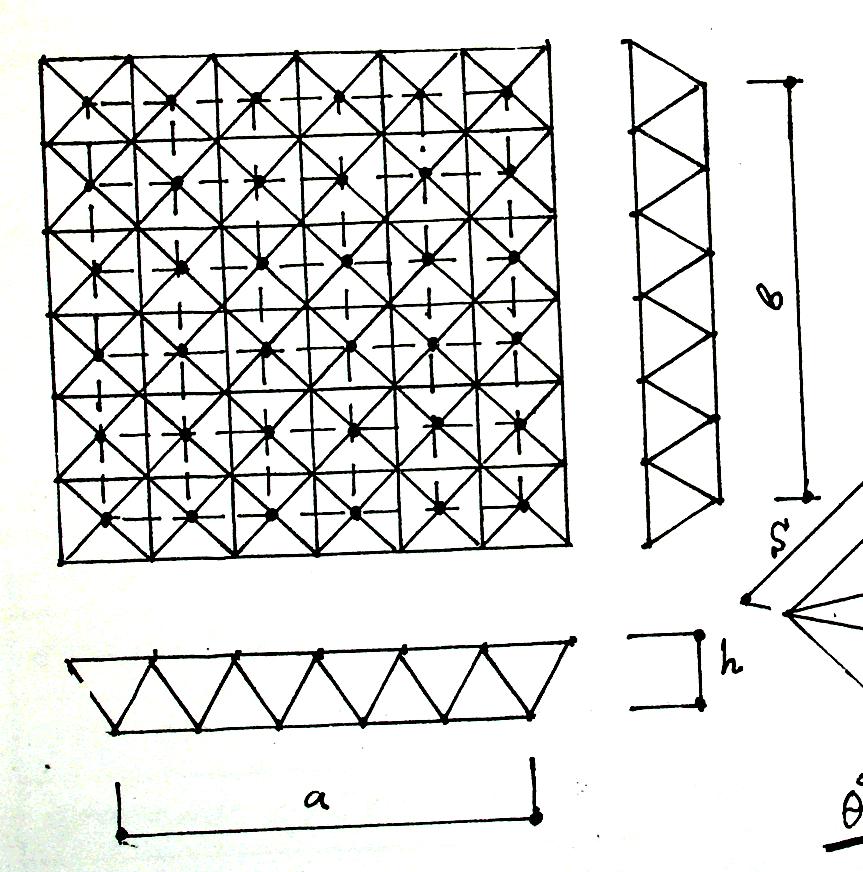g = gº∙1м – приведенная погонная нагрузка.

Рис.17

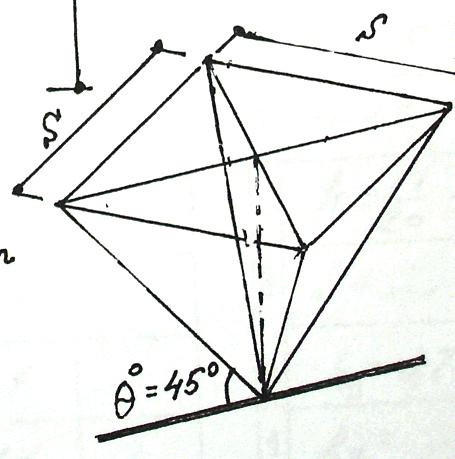
. . . . . . . . . . . . . . . . . . . . . . . . Плита с поясными сетками из равносторонних треугольных ячеек

h=0,816∙s; при θº=55ºили 54,686º

пог

g= gº∙1м – приведенная погонная нагрузка.

Рис.18

a пог b пог

плита прямоугольная: MX=α1 ∙q ∙ а∙b; My=α1 ∙q ∙ b∙ а;

а пог b пог

V x=Ψ1∙q∙a; Vу=Ψ1∙q∙b;

a пог b пог

плита треугольная: MX=(α1 ∙q ∙ а∙b)/ 2; My=(α1 ∙q ∙ b∙ а) / 2;

а пог b пог

а=b; V x=Ψ1∙q∙a; Vу=Ψ1∙q∙b;

пог пог

плита секторной конфигурации: MX=αR ∙q ∙ R²; Mу=αT ∙q ∙ R²;

пог

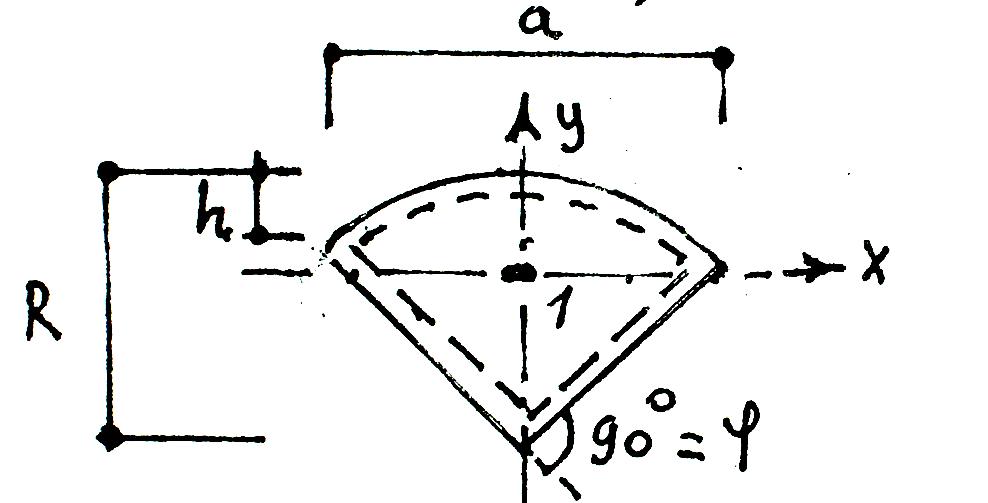V x,у=Ψ∙q∙R;

х пог у пог плита сегментной конфигурации: MX=α1 ∙q ∙ R²; Mу=α1 ∙q ∙ R²;

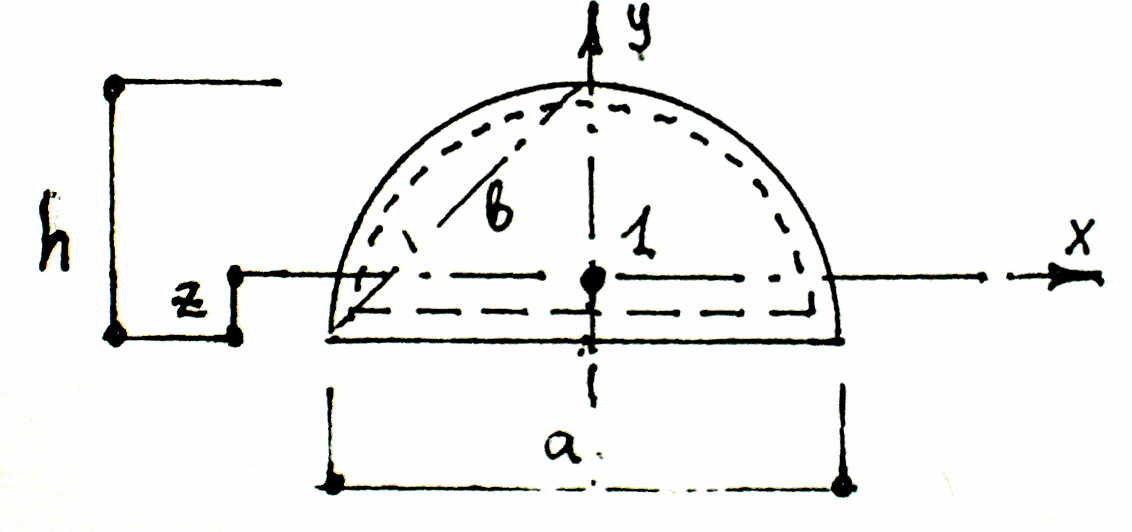пог

V x,у=Ψ∙q∙R;

Пог пог

плита круговой конфигурации: MX,у=α1 ∙q ∙ R²; V x,у=Ψ∙q∙R;

------------------------------------------------------------------------------------------

х,у

плита с прямоугольной ячейкой: Nп = ± 2,1 ∙ (M х,у ∙ s) / h;

х,у

Nр = ± 1,6 ∙ (V х,у ∙ s) / 2Sinθ;

θº=45º

s – расстояние между центрами узлов

поясной сетки.

х,у

плита с треугольной ячейкой: Nп = ± 1,3 ∙[ (0,866M х – 0,289 Mу) ∙ s] / h;

х,у

Nр = ± 1,6 ∙ (V ∙ s) / n∙Sinθ;

θº=55ºили 54,686º n – число опорных раскосов.

-----------------------------------------------------------------------------------------------------------------------------

A = Nmax / φ∙Ry ∙γc; - для сжатых стержней.

A = Nmax / Ry ∙γc; - для растянутых стержней.

λ ≤ 120 – сжатые опорные раскосы и стержни поясов.

λ ≤ 150 – сжатые раскосы решетки. ℓраскоса = h / Sinθ; Подсчет нагрузок на 1м2

Состав покрытия	qн н/м2	yf	q°н/м2
Защитный слой гравия на мастике-15, ρ=1800кг/м3	270	1,3
Трехслойный рулонный ковер	100	1,3
Пенопласт-60, ρ=60кг/м3	36	1,2
Оклеечная пароизоляция	30	1,3
Стальной профнастил	109	1,1
прогоны	29	1,1
Структурная плита	660	1,1
Подвесной потолок	150	1,1
снег		1,4
Итого:

исходные данные: пролет … ячейка … тип узлового соединения … конфигурация в плане … тип опирания … снег … RУ … и т.п.

пример 1:

плита с квадратной ячейкой, прямоугольной конфигурации в плане, опертая по контуру.

a пог b пог

MX=α1 ∙q ∙ а∙b; My=α1 ∙q ∙ b∙ а;

а,b

α1= 0,038; а / в=1; θº=45º

пог а,b

V=Qmax =Ψ ∙q ∙ a; Ψ =0,42;

х,у

Nп = ± 2,1 ∙ (M х,у ∙ s) / h;

х,у

Nр = ± 1,6 ∙ (V ∙ s) / 2Sinθ;

θº=45º

A = Nmax / φ∙Ry ∙γc; - для сжатых стержней.

A = Nmax / Ry ∙γc; - для растянутых стержней.

-----------------------------------------------------------------------------------------------

пример 2:

плита с квадратной ячейкой, прямоугольной конфигурации в плане, защемленная по контуру.

х a пог у b пог

M1=α1 ∙q ∙ а∙b; M1=α1 ∙q ∙ b∙ а;

пог пог

M2=α2 ∙q ∙ а∙b; M3=α2 ∙q ∙ b∙ а;

а,b

α1 = 0,018; α1 = 0,042; Ψ=0,25

пог

V=Qmax =Ψ ∙q ∙ a; а / в=1;

х,у

Nп = ± 2,1 ∙ (M х,у ∙ s) / h;

х,у

Nр = ± 1,6 ∙ (V ∙ s) / 2Sinθ;

θº=45º

A = Nmax / φ∙Ry ∙γc; - для сжатых стержней.

A = Nmax / Ry ∙γc; - для растянутых стержней.

---------------------------------------------------------------------------------------------------

пример 3:

плита с треугольной ячейкой, прямоугольной конфигурации в плане, опертая по четырем углам. х a пог у b пог

M1=α1 ∙q ∙ а∙b; M1=α1 ∙q ∙ b∙ а;

пог

M2=α2 ∙q ∙ а∙b;

α1 = 0,011; α2 = 0,16; Ψ=0,25

а пог

V=Qmax =Ψ ∙q ∙ a; а / в=1;

Nр = ± 1,6 ∙ (V ∙ s) / 2Sinθ; θº=55º

Nп = ± 1,3 ∙[ (0,866M х – 0,289 Mу) ∙ s] / h;

A = Nmax / φ∙Ry ∙γc; - для сжатых стержней.

A = Nmax / Ry ∙γc; - для растянутых стержней.

пример 4:

плита с треугольной ячейкой, прямоугольной конфигурации в плане, защемленная по трем сторонам со свободно висящим краем.

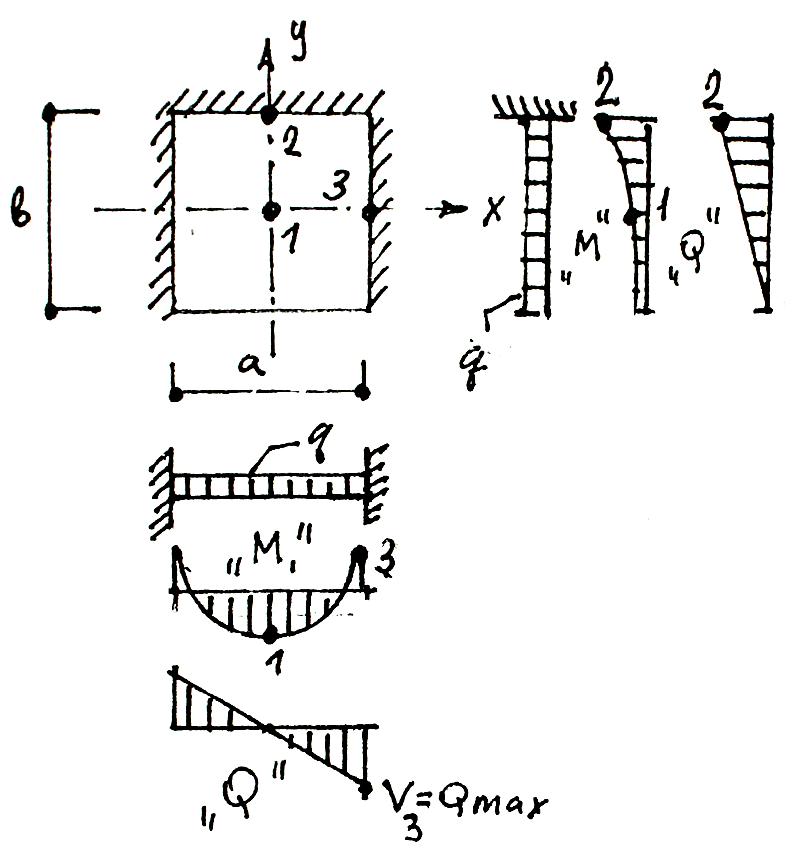
х a пог у b пог

M1=α1 ∙q ∙ а∙b; M1=α1 ∙q ∙ b∙ а;

пог пог

M3=α3 ∙q ∙ а∙b; M2=α2 ∙q ∙ b∙ а;

а в

α1 = 0,048; α1 = 0,01;

α2 = 0,05; α3 = 0,084;

Ψ=0,28; V= Ψ ∙q ∙ a;

Nр = ± 1,6 ∙ (V ∙ s) / 2Sinθ; θº=55º

Nп = ± 1,3 ∙[ (0,866M х – 0,289 Mу) ∙ s] / h;

A = Nmax / φ∙Ry ∙γc; - для сжатых стержней.

A = Nmax / Ry ∙γc; - для растянутых стержней.

----------------------------------------------------------------------------------------------------

пример 5:

плита с треугольной ячейкой, треугольной конфигурации в плане, опертая по контуру.

а пог b пог

MX,1=(α1 ∙q ∙ а∙b)/ 2; My,1=(α1 ∙q ∙ b∙ а) / 2;

пог

а=b; V =Ψ ∙q ∙ a; Ψ=0,17;

а в

α1 = 0,043; α1 = 0,034;

Nр = ± 1,6 ∙ (V ∙ s) / 2Sinθ; θº=55º

Nп = ± 1,3 ∙[ (0,866M х – 0,289 Mу) ∙ s] / h;

A = Nmax / φ∙Ry ∙γc; - для сжатых стержней.

A = Nmax / Ry ∙γc; - для растянутых стержней.

----------------------------------------------------------------------------------------------------

пример 6:

плита с прямоугольной ячейкой, секторной конфигурации в плане, опертая по контуру.

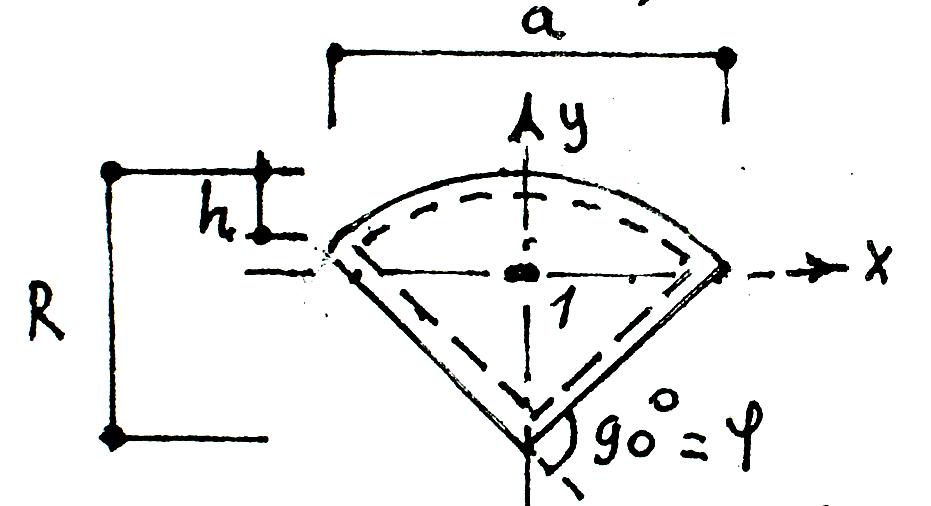пог пог

: MX=αR ∙q ∙ R²; Mу=αT ∙q ∙ R²;

пог

V x,у=Ψ ∙ q ∙ R; αR=0,0366;

αT=0,0339; Ψ=0,35;

Aсектора = π∙R²φº/ 360º =0,00873∙R²∙φº; a = 2R∙Sin 0,5φ;

ℓдуги= 0,1745∙R∙φº; h= 0,5a∙tg0,25φ;

Nп, Nр ,A – смотри вариант 1.

пример 7:

плита с прямоугольной ячейкой, сегментной конфигурации в плане, опертая по контуру.

х пог у пог

MX,1 =α1 ∙q ∙ R²; Mу,1 =α1 ∙q ∙ R²;

х у

α1 = 0,0311; α1 = 0,0785; h = R = 0,5a;

пог

V x,у=Ψ ∙ q ∙ R; Ψ=0,426;

Aсегмента = h / 15 ∙(6a+8b) = 0,392∙a²; Ζ=0,2122∙a;

Или Aсегмента =R²/ 2∙[π∙φ/ 180º - Sinφ];

ℓдуги= √ (a²+16/ 3∙h²);

Nп, Nр ,A – смотри вариант 1.

---------------------------------------------------------------------------------------------------

Пример 8:

плита с прямоугольной ячейкой, круговой конфигурации в плане, опертая по контуру.

MX,у,1 =α1 ∙q ∙ R²; V x,у=Ψ∙q∙R;

α1 = 0,1875; Ψ=0,5;

Nп, Nр ,A – смотри вариант 1.

--------------------------------------------------------------------------------------------------