4.3. Решение типовых задач

4.3.1. За январь имеются следующие данные о заработной плате продавцов по четырем секциям торгового дома:

секции	заработная плата, рублей x	количество продавцов f	фонд оплаты труда, рублей xi fi
1	25000	5	125000
2	25060	3	75180
3	25140	5	125700
4	25320	3	75960
Итого		16	401840

Вычислите среднюю месячную заработную плату по четырем секциям в целом.

Решение:

Обозначим заработную плату через x, а количество продавцов через f. Логическая формула средней величины имеет следующий вид:

Средняя заработная плата =

Фонд оплаты труда (ФОТ) каждой секции представляет собой произведение заработной платы на количество продавцов этой секции,

т.е. .

Чтобы определить ФОТ по всему торговому предприятию, необходимо исчислить фонды по каждой секции, затем их суммировать.

Средняя заработная плата одного продавца в целом по торговому предприятию за месяц будет равна отношению этой суммы и численности продавцов всех секций.

Так как ФОТ равен произведению варианты на частоту, то, в этом случае, для определения средней величины применяется формула средней арифметической взвешенной. Обоснованную логическую формулу выразим алгебраически через соответствующие обозначения:

= = , где:

x - ФОТ первой секции,

f₁ - численность продавцов первой секции,

x₂f₂ - ФОТ второй секции,

f₂ - численность продавцов второй секции и т.д.

Теперь произведем расчет средней заработной платы одного продавца по формуле средней арифметической взвешенной:

= = = = 25115 руб.

Средняя заработная плата одного продавца, рассчитанная по формуле средней арифметической взвешенной, за январь равна 25115 руб.

Какой экономический смысл заключается в формуле средней арифметической взвешенной?

В числителе вполне определенная величина: ФОТ; в знаменателе – численность всех продавцов. Отношение числителя и знаменателя дает среднюю величину. Важно подчеркнуть это обстоятельство для того, чтобы уяснить экономическую связь между реальными показателями и средней взвешенной величиной. Она связана с общим размером ФОТ: если среднюю величину 25115 руб. умножить на число продавцов 16, то должны получить общий размер фонда оплаты труда (25115*16=401840 руб.).

ФОТ – величина, которая является определяющим показателем и от которой зависят форма и величина средней величины.

4.3.2. По данным таблицы требуется определить средний процент студентов университета, направленных на обучение организациями:

отделение университета	всего студентов, чел.	из них, направленные на обучение организациями, %
заочное	360	75
очное	720	90
Итого	1080

Решение:

Вариантами (х) в данном случае являются проценты направленных студентов на обучение организациями потребительской кооперации, а весами или частотами (f) – количество студентов на каждом отделении.

Средний процент направленных студентов на обучение кооперативными организациями в целом по университету равен:

= = = = 85%

4.3.3. За два месяца по предприятиям района имеются следующие данные:

№ предприятия	сентябрь		октябрь
	численность работников	средняя месячная заработная плата, руб.	средняя месячная заработная плата, руб.	фонд заработной платы, руб.
1	140	23560	23600	3186000
2	200	23600	23580	4951800
3	260	23330	23340	5835000

Определите, за какой месяц и на сколько процентов была выше средняя месячная заработная плата работников предприятия.

Решение:

Введем условные обозначения для сентября:

f - численность работников по каждому предприятию;

x- средняя месячная заработная плата работников каждого предприятия.

Определяющий показатель – общий фонд заработной платы - .

Средняя месячная заработная плата работников предприятия за сентябрь составила:

= = = = 23473,7 руб.

Условные обозначения для октября следующие:

w - фонд заработной платы по каждому предприятию;

x – средняя месячная заработная плата работников каждого предприятия.

Определяющий показатель - .

Средняя заработная плата в октябре исчисляется по формуле средней гармонической взвешенной:

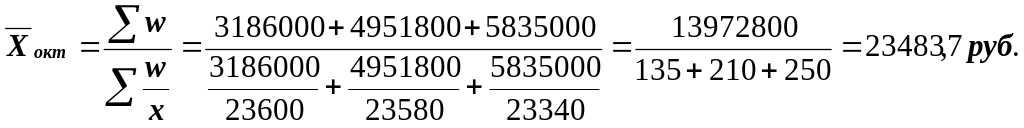
где: - численность работников каждого предприятия в октябре.

Динамика средней месячной заработной платы работников предприятий:

или 100,3%.

Следовательно, средняя месячная заработная плата работников предприятий в октябре повысилась на 0,3% по сравнению с сентябрем (100,3% - 100%).

4.3.4. В таблице имеются данные о дневной выработке деталей рабочими цеха (графы 1-2):

дневная выработка, шт. (х)	число рабочих (f)	среднее значение интервала (x )	произведение середины интервала на число рабочих (x f)
1	2	3	4
до 100	20		1800
100-120	30		3300
120-160	40		5600
160 и более	10		1800
Итого:	100	-	12500

(в графах 3-4 данной таблицы уже выполнены предварительные расчеты для решения задачи).

Определите среднедневную выработку рабочих цеха.

Решение:

Так как предварительные расчеты уже сделаны в таблице, то среднедневную выработку рабочими цеха, находим по формуле средней арифметической взвешенной:

= = деталей

Следовательно, рабочие цеха делают в среднем 125 деталей в день.

4.3.5. Определите моду по данным таблицы:

Распределение размеров женской обуви,

проданных в обувном отделе торгового объединения, в ноябре 2010 г.

размер женской обуви (х)	число проданных пар, % к итогу (f)
А	1
33	4
34	12
35	18
36	26
37	20
38	13
39	6
40	1
Итого	100

Решение:

По данным таблицы видно, что наибольшая частость (f =26) приходится на 36-й размер обуви.

Следовательно, мода (Мо) равна 36-му размеру, т.е. в данной совокупности именно этот размер обуви в ноябре 2010 года пользовался наибольшим спросом у женского населения.

4.3.6. По данным о содержании влаги в поступившей партии товара в магазин, определите моду:

влажность, % (х)	число образцов (f)	накопленная частота S	середина интервала x	x f
А	1	2	3	4
до 14	20	20	13	260
14-16	30	50	15	450
16-18	25	75	17	425
18-20	15	90	19	285
20 и более	10	100	21	210
Итого	100	-	-	1630

Решение:

По данным таблицы, наибольшей влажностью обладают товары в интервале 14 - 16% (графа 1). Это и есть модальный интервал, величина интервала i = 2 (16 - 14), нижняя граница х = 14, частота f_Мо = 30, предмодальная частота f_Мо-1 = 20, а послемодальная частота f_Мо+1 = 25.

Модальный процент влажности в партии товара составляет:

Мо = х₀ + i = 14 + 2 =15,3%

Таким образом, в данной совокупности поступившей партии товаров наибольший процент влажности приходится на 15,3%.

4.3.7. Определите медиану интервального ряда по данным о содержании влаги в поступившей партии товара в магазин:

влажность, % (х)	число образцов (f)	накопленная частота S
А	1	2
до 14	20	20
14-16	30	50
16-18	25	75
18-20	15	90
20 и более	10	100
Итого	100	-

Решение:

Для определения медианы в интервальном ряду сначала находим номер медианы:

N = = 50,5%

Накапливаем частоты (графа 2 таблицы) и определяем, что 50,5 образцов товара приходится на интервал (16 – 18).

Точное нахождение медианы на данном интервале определим по формуле:

= 16+2 = 16%

Таким образом, половина (50%) партии товара имеет влажность менее 16%, и половина (50%) имеет содержание влаги в партии товара выше 16%.