4 Анализ быстродействия пи-регулятора

Операторная передаточная функция ПИ-регулятора состоит из интегрирующего и форсирующего звеньев:

Для обеспечения оптимальной по быстродействию настройки ПИ-регулятора постоянную времени надо принять равной по величине наибольшей из постоянных времени апериодических звеньев САУ . в этом случае форсирующее звено регулятора нейтрализует наиболее инерционное апериодическое звено САУ.

Передаточная функция замкнутой системы, при выбранной настройке ПИ-регулятора, соответствует колебательному звену 2-го порядка, поскольку передаточные функции форсирующего звена регулятора и апериодического звена с постоянной времени в формуле (1) можно сократить:

. (19)

Приведенные параметры САУ с ПИ-регулятором определяются в результате приведения передаточной функции (19) к табличному виду колебательного звена 2-го порядка:

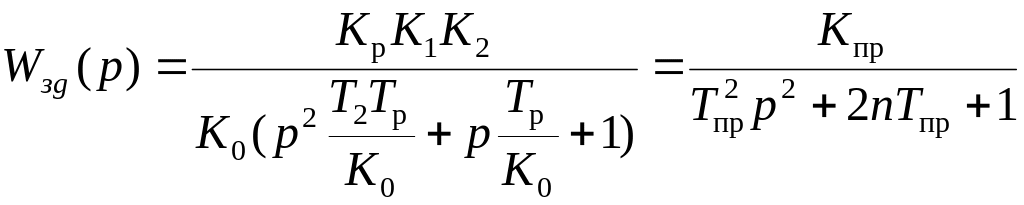(20)

Общий коэффициент усиления системы K₀ определяется формулой (4), приведенный коэффициент усиления колебательного звена 2-го порядка K_пр – формулой:

;

приведенная постоянная времени колебательного звена:

; (21)

коэффициент затухания:

. (22)

Величину общего коэффициента усиления К₀, при котором переходная функция имеет апериодический характер, можно определить из формулы (22) при n=0,5:

. (23)

Приведенная постоянная времени колебательного звена 2-го порядка для n=0,5 будет равна:

. (24)

Отсюда длительность изменения переходной функции замкнутой системы, характеризующая быстродействие ПИ-регулятора, определится временем

. (25)

Из сравнения формул (11) и (27) видно, что быстродействие ПИ-регулятора незначительно хуже по сравнению с П-регулятором. Однако его преимущество заключается в отсутствии ошибки регулирования в установившихся режимах.

4 Анализ быстродействия и-регулятора

Операторная передаточная функция И-регулятора состоит из интегрирующего звена с коэффициентом усиления : . После подстановки в выражение (1) передаточной функции и преобразования получена передаточная функция САУ с И-регулятором, характеризующая систему 3-го порядка:

. (26)

Для приведения передаточной функции (25) к табличным передаточным функциям типовых структурных звеньев выполнено преобразование:

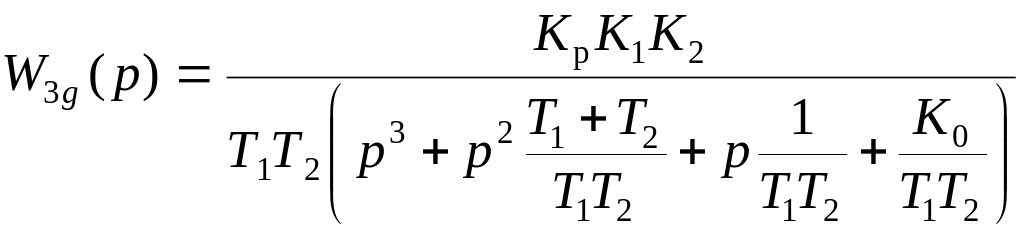. (27)

В выражении (27) общий коэффициент усиления системы К₀ определяется формулой (4). Полученную передаточную функцию (27) можно привести к эквивалентным апериодическому звену 1-го порядка и колебательному звену 2-го порядка. Приведение звеньев можно выполнить посредством вычисления корней кубического полинома знаменателя передаточной функции (27): p₁ = -; p_2,3 = -  j и последующего разложения этого полинома на множители. Передаточная функция, приведенная к двум структурным звеньям, имеет вид:

(28)

Параметры приведенных звеньев - апериодического 1-го порядка и колебательного 2-го порядка - определяются следующими формулами:

; ; .

Для оценки соотношения приведенных постоянных времени и можно принять с некоторым приближением вещественный корень кубического полинома равным по модулю коэффициенту при квадратичном члене полинома

. (29)

Тогда приведенная постоянная времени Т_1пр будет равна обратной величине этого коэффициента:

. (30)

Приведенная постоянная времени Т_2пр и коэффициент затухания n колебательного звена 2-го порядка в значительной мере зависят от постоянных времени Т₁ и Т₂ апериодических звеньев и общего коэффициента усиления системы К₀. Апериодический характер переходной функции колебательного звена с коэффициентом затухания n=0,5 возможен при общем коэффициенте усиления, определяемом выражением:

. (31)

Тогда после некоторых преобразований свободного члена кубического полинома передаточных функций (27) и (28) получено соотношение:

С использованием формул (29) и (31) можно получить приближенную формулу для приведенной постоянной времени колебательного звена 2-го порядка с коэффициентом затухания n=0,5:

. (32)

Отсюда длительность изменения переходной функции замкнутой системы, характеризующая быстродействие ПИ-регулятора, определится выражением:

. (33)

Из соотношения выражений (30) и (32) видно, что приведенная постоянная времени колебательного звена Т_2пр существенно больше постоянной времени Т_1пр апериодического звена 1-го порядка. Поэтому длительность изменения переходной функции замкнутой системы до установившегося значения характеризуется приведенной постоянной времени колебательного звена Т_2пр. Из (32) следует, что эта приведенная постоянная времени определяется суммой существенных постоянных времени апериодических звеньев 1-го порядка САУ. Следовательно, быстродействие И-регулятора, характеризуемое интервалом времени будет существенно хуже по сравнению с П-регулятором.