2.9 Устойчивость сжатых стержней

При сжатии стержней при достижении критической сжимающей нагрузки F_кр происходит потеря устойчивости – стержень искривляется и самостоятельно не может занять прежнее прямолинейное положение (рис.2.18). Напряжение в сжатом стержне σ = F / А. В зоне упругих деформаций величина критической силы определяется по формуле Эйлера:

Рис.2.18

Критическое напряжение: , при σ_кр ≤ σ_у,

где μ – коэффициент приведения длины, определяется способом закрепления стержня; J_min – минимальный осевой момент инерции сечения, Е – модуль упругости материала; λ = μ l / i_min – гибкость стержня; минимальный радиус инерции сечения.

В зоне пластических деформаций: σ_у < σ_кр ≤ σ_т, σ_кр = а – вλ, F_кр = σ_кр · А, где а, в - константы, определяются материалом стержня (зависимость Ясинского).

Расчёты на устойчивость проводятся на основе неравенства устойчивости:

,

где [ σ _y] = σ_кр / n_y – допускаемое напряжение на устойчивость; n_y – коэффициент запаса устойчивости (приблизительно на 20-30% больше коэффициента запаса прочности).

Для практических расчётов при λ ≥ 100; [σ_y] = φ [σ_сж], где [σ_сж] – допускаемое напряжение на сжатие; φ = φ (материал, λ) – коэффициент уменьшения допускаемых напряжений на сжатие, приводится в таблицах.

Литература: [2, стр.483…493]; [5, стр.413…425].

2.10 Определение напряжений и деформаций при действии циклических и динамических нагрузок

Циклические нагрузки.

При действии циклических нагрузок напряжения в общем случае изменяются по синусоидальному закону:

 = _m + _а sin t,

где _m - среднее значение напряжения, _а – амплитуда напряжений.

_max,  _min , _m = (_max + _min ) / 2, _а = (_max - _min) / 2 – основные параметры цикла (рис.2.19, 2.20).

R = _min / _max - коэффициент асимметрии цикла.

Наиболее распространенные циклические напряжения:

Симметричный цикл (рис.2.19):

R_ = -1, _m = 0

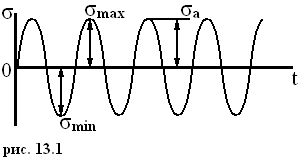
Рис.2.19 Рис.2.20

От нулевой или пульсирующий цикл (рис.2.20):

R_ = 0; _m = _a / 2,

где R_ = _min / _max - коэффициент асимметрии цикла.

Сопротивление материалов циклическим нагрузкам значительно меньше чем при статических нагрузках.

Усталость – процесс постепенного накапливания необратимых изменений физико-механических свойств (в основном, это рост микротрещин) под действием циклических нагрузок. Прочность при действии циклических нагрузок по симметричному циклу определяет предел выносливости.

Кривая усталости – строится на основе экспериментов. Черные металлы имеют физический предел выносливости, остальные металлы условный (рис.2.21).

1 – кривая выносливости для черных металлов,

2 – для цветных.

Рис.2.21

Здесь _а - амплитуда напряжений при испытаниях, N – число циклов до разрушения.

Откуда  ^m N = const, при N N_ , где N_ - базовое число циклов (для сталей, чугунов N_ =10⁶ – 10⁷, m= 4 – 10).

Предел выносливости (_-1 - для симметричного цикла) – максимальная амплитуда напряжений, при котором образец выдерживает неограниченное число циклов, не разрушаясь.

У словный предел выносливости – амплитуда напряжений, при которой образец выдерживает 10⁸ циклов до разрушения - _-1^y.

При действии произвольной циклической нагрузки прочность материала оценивается на основе диаграмм предельных амплитуд. Она строится на основании экспериментов, аналогичных при построении кривой усталости при различных значениях _m , из которых определяется величина амплитуды _а и постоянной составляющей _m, при которых материал выдерживает базовое число циклов N_{ .}

На усталостную прочность оказывает влияние:

а) концентрация напряжений через эффективный коэффициент концентрации:

K_ = _-1 / '_-1;

б) абсолютные размеры детали через масштабный коэффициент:

_ = '_-1 / _-1 ,

в) состояние поверхности детали через коэффициент состояния поверхности;

_ = '_-1 / _-1 ,

где '_-1 - предел выносливости образца с концентратором, размерами и состоянием поверхности детали, _-1 - предел выносливости стандартного образца.

Коэффициент запаса детали, работающей при циклическом нагружении:

 = _m + _а sint , определяется по формуле:

По аналогии для деталей, работающих при циклических касательных напряжениях:

При совместном действии нормальных и касательных напряжений коэффициент запаса прочности определяется по формуле:

Если n  n , где n - допускаемое значение коэффициента запаса, то деталь или элемент конструкции выдержит нагрузку в течение базового числа циклов.

Для многих деталей машин n  1,5 – 2,5