2.7 Геометрические характеристики плоских сечений

Сопротивление элемента конструкции разрушению и деформированию определяется не только материалом, из которого изготовлен (он определяет допускаемые напряжения), но и формой сечения. Основные геометрические характеристики сечений элементов конструкций, которые определяют их сопротивление нагрузкам (рис.2.13).

1) Площадь сечения: ,(мм²).

2) Статический момент:

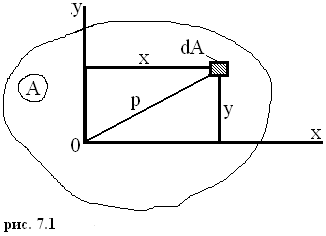
, (мм³)

, (мм³)

3) Осевые моменты инерции:

- относительно оси x:

, (мм⁴);

- относительно оси y:

(мм⁴). Рис.2.13

4) Полярный момент инерции: (мм⁴).

5) Центробежный момент инерции: (мм⁴).

Т.к. , то .

6) Момент сопротивления сечения осевой

(мм³), используются при решении задач на изгиб.

Момент сопротивления сечения полярный

(мм³), используется при решении задач на кручение.

5) Радиусы инерции (мм).

Литература: [2, стр. 135…154]; [5, стр. 121…132].

2.8.Определение напряжений и деформаций при статическом нагружении

В основе лежит гипотеза плоских сечений – сечения после деформации остаются плоскими и перпендикулярными оси бруса. В тех деформациях, где эта гипотеза экспериментально подтверждается, можно получить теоретически выражения для распределения напряжений по сечению и для распределения деформаций по оси бруса.

Растяжение (сжатие).

Закон распределения напряжений в поперечном сечении равномерный, т.е. во всех точках сечения напряжения одинаковы (рис 2.14): σ = N / A ≤ [σ ] – условие прочности при растяжении – сжатии. Перемещение сечения с координатой x относительно начального сечения:

Удлинение (укорочение) участка длиной l: ∆l = δ_x=l

По закону Гука ∆l =N ∙ l / E ∙ A

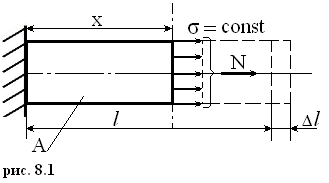
Рис.2.14 Рис.2.15

Сдвиг.

Закон распределения напряжений условно принят равномерным: τ =Q/A_сдв

Условие прочности при сдвиге:

Определение поверхности сдвига:

Определение максимальной силы сдвига:

Кручение.

Гипотеза плоских сечений подтверждается только для бруса круглого сечения (рис.2.16).Касательное напряжение в любой точке сечения (рис.2.16 а)

τ_ρ = ( M_k / J_p ) ρ ,

Максимальные напряжения возникают на контуре сечения где ρ - радиус точки, в которой определяются напряжения, J_p – полярный момент инерции сечения (для круглого сечения

J_p =  d ⁴ / 32 = 0,1d).

τ_max = M / W

где W_p = J_p /(d/2) -полярный момент сопротивления (W_ρ= =  d³ / 16 = 0,2d³ ).

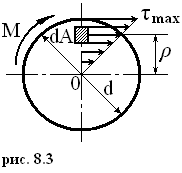
Рис.2.16 а

Условие прочности при кручении:

Диаметр вала из условия прочности:

Максимальный момент:

Угол закручивания сечения с координатой x относительно начального (рис.2.16 б)

, при х = l

Рис.2.16 б

Плоский изгиб.

Закон распределения нормальных напряжений (рис.2.17) в сечении балки вдоль оси У

σ = ( M_z / J_z ) y,

где y – координата точки, в которой определяется напряжение, J_z - осевой момент инерции сечения.

Максимальные напряжения возникают в наиболее удаленных точках сечения:

σ _max = M / W_z

где W_z = J_z / (h / 2) - осевой момент сопротивления сечения.

Д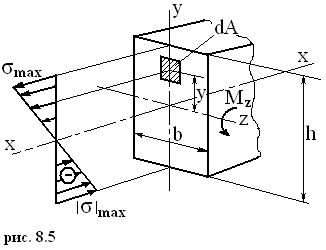 ля прямоугольного сечения J_z = bh³ / 12; W_z = bh² / 6; для круглого сечения J_z = d ⁴ / 64 ; Wz = d³/32 = 0,1d³. Для двутавров, швеллеров, уголков – значения J, W приведены в таблицах.

Рис.2.17

Условие прочности при изгибе:

Литература:  3, стр.20…44; 70…72; 91…99; 135…147.