Розрахунково-проектувальна робота №11

“Розрахунок статично невизначенї арки”

Таблиця 12	EI0 ESIS	12	0	0	0.30	0.35	0	0	0.40	0.45	0	0.25
	Обриси осі арки	11	Коло	Парабола	Коло	Парабола	Коло	Парабола	Коло	Парабола	Коло	Парабола
	Номер Схеми	10	1	1	2	2	1	1	2	2	1	2
	Остання цифра шифру	9	1	2	3	4	5	6	7	8	9	0
	q2, кН/м	8	0	12	0	14	0	13	0	11	0	18
	q1, кН/м	7	20	0	18	0	17	0	15	0	16	0
	f/L	6	0.20	0.30	0.40	0.15	0.18	0.25	0.35	0.22	0.14	0.16
	Друга цифра шифру	5	1	2	3	4	5	6	7	8	9	0
	F1, кН	4	50	60	70	80	100	65	75	85	90	40
		3	0,4	0,6	0,8	0,2	0,5	0,4	0,8	0,6	0,2	0,5
	L, м	2	18	20	22	24	25	26	28	30	32	34
	Перша цифра шифру	1	1	2	3	4	5	6	7	8	9	0

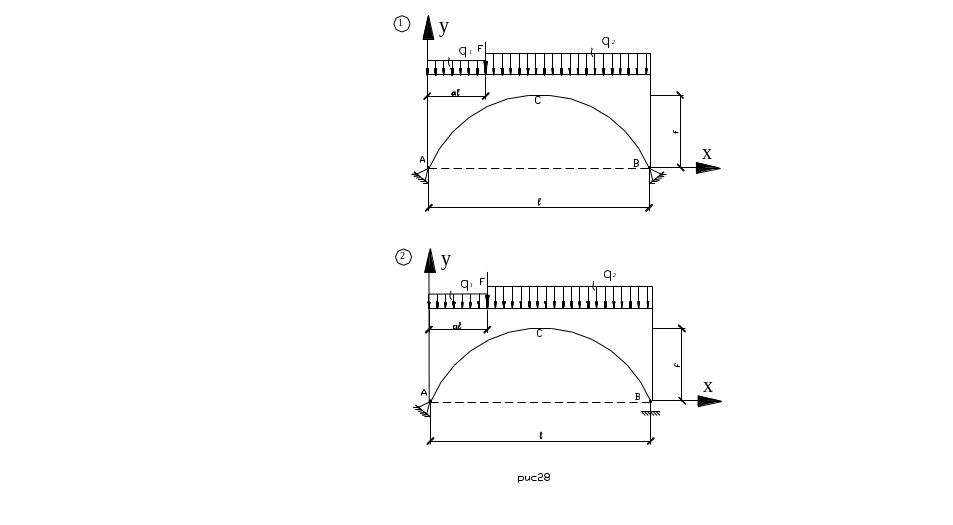
Для двохшарнірної арки з затяжкою, або без, вибраної згідно з шифром (рис. 28):

1. Побудувати епюру згинальних моментів та перевірити її.

2. Побудувати епюру поперечних сил та перевірити її.

3. Побудувати епюру поздовжніх сил та виконати перевірку.

Вихідні дані вибрати з табл. 12.

Методичні вказівки

Обриси осі арки та кути нахилу дотичних повинні бути отримані у відповідності з методичними вказівками до РПР №4.

Для скорочення об’єму обчислень можна обмежитись семи точок осі арки, включаючи два опорних шарніра.

В основній системі для двохшарнірної арки за зайве невідоме необхідно прийняти горизонтальну реакцію в одній з опор (розпір); для арки з затяжкою – зусилля в затяжці. В цьому випадку в одиничному та вантажному станах згинальні моменти та поперечні сили визначаються за формулами:

де М і Q – згинальні моменти та поперечні, обчислені як в балці на двох опорах. Епюри цих зусиль будуються до визначення коефіцієнтів.

Коефіцієнти канонічних рівнянь обчислюють за формулами:

Всі математичні операції, пов’язані з обчисленням коефіцієнтів, вільних членів та з визначенням зусиль арці, краще проводити в табличній формі. В залежності від обрисів осі арки рекомендується наступна форма таблиць:

а) при обрисі осі арки по параболі

Початок таблиці

Номер точки	X	l-X	x(l-x)	y=4fx(l-x)/l2	l-2x	Tg=4f(l-2x)/l2		sin	cos
1	2	3	4	5	6	7	8	9	10

в) при обрисі осі арки по колу

Початок таблиці

Номер точки	X	l/2-X	(l/2-X)2	[R2-(l/2-x)2]1/2	y=[R2-(l/2-x)2]1/2-R+f	l-2x	sin=l-2x/2R	y+R-f	Cos=(y+R-f)/R
1	2	3	4	5	6	7	8	9	10

Продовження таблиці незалежно від обрисів осі арки

Номер точки	X cos4	Y2	Y2X cos4	Mp Kн м	Mp YX cos4	-YX1	M=Mp-YX1	Mp Y2X cos4
1	11	12	13	14	15	16	17	18

Номери точок	Qp,кН	Qp cos	X1sin	Q=Qpcos - X1sin	Qpsin	X1cos	N=-(Qpsin+ X1cos)
1	19	20	21	22	23	24	25

Поперечний переріз арки приймається прямокутнім з висотою, що змінюється за законом d=dxcos де dx- висота перерізу в середині прольоту.

Якщо розділити вісь арки на відрізки з їх рівними проекціями то S= Враховуючи що І= для коефіцієнтів ₁₁ і _1р можна отримати наступні вирази:

;

В розрахунковій таблиці передбачено обчислення в стовпчику 11, обчислення в стовпчику 13, а також обчислення в стовпчику 15 . Сума величин стовпчика 15 дає значення , а сума величин стовпчика 13 - значення .

Для арки з затяжкою до суми величин стовпчика 13 необхідно додати величину , де E_S і A_S - модуль пружності та площа поперечного перерізу затяжки. Цим самим враховується деформація затяжки. Таким чином, для арки з затяжкою коефіцієнт визначиться за формулою

Невідоме X₁ можна визначити за формулою:

Після цього необхідно обчислити зусилля в арці за формулами:

;

;

.

В наведеній вище табличці передбачено обчислення М /стовпчики 14,16,17/ Q /стовпчики 19=22/ та N / стовпчики 19,23-25/. При обчисленні поперечного та поздовжнього зусиль в перерізі, де діє зовнішня зосереджена сила, необхідно врахувати стрибок Qр в цьому перерізі на величину Fcos

Перевірка правильності розрахунків ведеться за допомогою стовпчика 18. Сума значень цього стовпчика повинна забезпечити виконання умови:

Для арки з затяжкою ця сума повинна бути рівна величині:

Розрахунково-проектувальна робота №12

“Розрахунок статично невизначеної ферми”

для статично невизначеної ферми, вибраної згідно з шифром (рис. 29), визначити внутрішні зусилля в усіх стержнях ферми від заданого навантаження. Вихідні дані вибрати з таблиці 13.

Таблиця 13

Перша цифра шифру	d, м	Площа перерізу		Дру-га циф-ра ши-фру	F kH	Площа перерізу		Остан-ня цифра шифру № схеми	h м
		Нижньо-го поясу	Верхньо-го поясу			Ре-шітки	Еле-мен-тів шпренгеля
1	2	3	4	5	6	7	8	9	10
1	3,0	А	2А	1	40	0,4А	А	1	3,0
2	3,2	0,9А	1,9А	2	50	0,5А	1,2А	2	3,1
3	3,4	0,8А	1,8А	3	60	0,6А	1,3А	3	3,2
4	3,6	0,7А	2,1А	4	70	0,7А	1,1А	4	3,3
5	3,8	0,6А	2,2А	5	80	0,8А	1,4А	5	3,4
6	2,6	1,1А	2,4А	6	100	А	1,5А	6	3,5
7	2,8	1,2А	2,5А	7	120	1,1А	1,6А	7	3,6
8	3,1	0,85А	1,7А	8	90	0,9А	1,7А	8	3,7
9	3,5	0,75А	1,6А	9	30	0,6А	1,9А	9	3,8
0	3,7	0,65А	1,5А	0	110	0,5А	1,8А	0	2,8

Ступінь статичної невизначеності ферми необхідно визначити у відповідності з методичними вказівками до теми 10.

Основну систему виберіть симетричною, що значно скорочує об’єм обчислень. Якщо за невідоме приймають зусилля в стержні, то цей стержень не відкидають і зусилля в ньому враховують при обчисленні головних коефіцієнтів.

Використовуючи симетрію, в розрахунок можна включити тільки половину ферми; стержні що не мають пари в другій половині, приймають вдвічі коротшими.

Коефіцієнти та вільні члени методу сил підраховують за формулою Мора, враховуючи тільки поздовжні сили. Враховуючи що площа поперечного перерізу та модуль пружності по довжині кожного стержня є сталими величинами, інтегрування можна замінити сумою:

Тут - зусилля в стержні основної системи від дії одиничного навантаження;

- зусилля в стержнях основної системи ферми від дії зовнішнього навантаження.

Всі розрахунки вигідно проводити в табличній формі:

Номер стержня	l,м	A0/A	N1	NP, kH	N1lA0/A	N21lA0/A	N1 NPlA0/A	N1X1	N=NP+N1X1	перевірка N N1lA0/A
1	2	3	4	5	6	7	8	9	10	11
Сума =						11EA0	1PEA0

За величину А₀ необхідно прийняти А з таблиці. Розтягуюче зусилля в стержні в стержні повинно прийматися зі знаком “+”, а стискуюче – зі знаком “-”.

Сума величин в стовпчику 7 дає значення коефіцієнта канонічного рівняння методу сил , а в стовпчику 8- значення вантажного коефіцієнта Невідоме визначаємо за формулою:

= -

Після цього можна визначити значення N (стовпчик 10) та виконати кінематичну перевірку =0 (стовпчик 11), помилка не повинна перевищувати 2%